Anand Classes provides NCERT Solutions and Notes for Class 11 Chemistry Chapter 4 (Chemical Bonding and Molecular Structure), Questions Q4.31 to Q4.40, with step-by-step explanations, illustrative diagrams, and key point highlights. These solutions cover essential topics such as Molecular Orbital Theory, Hybridisation, VSEPR, Bond Order, Polarity, Magnetic Properties, and Molecular Shapes, designed in line with CBSE exam style and useful for JEE & NEET preparation. Students can view or download a printable PDF of the notes and solutions free of cost. Click the print button to download study material and notes.
Q : What do you understand by bond pairs and lone pairs of electrons ? Illustrate by giving one example of each type?
Covalent bonds are formed by mutual sharing of electrons between two atoms.
The shared pairs of electrons present between bonded atoms are called bond pairs.
All the valence electrons of an atom may not participate in bonding. The valence electron pairs not involved in bonding are called lone pairs of electrons.
Example
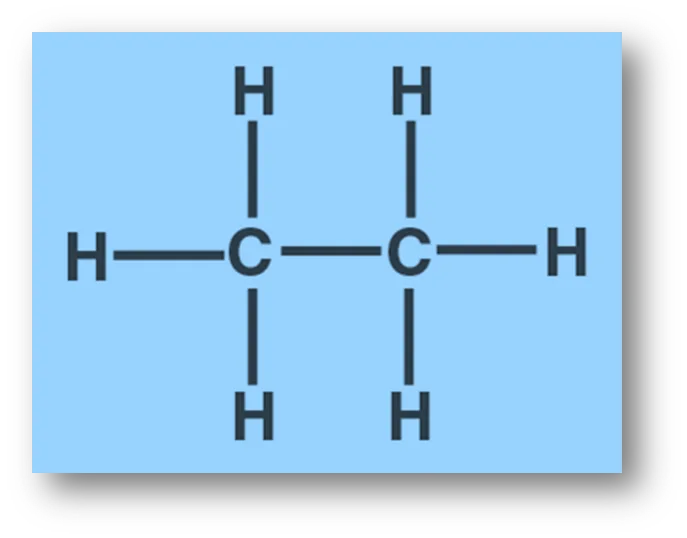
In ethane (C2H6): Ethane has 7 bond pairs but zero lone pair.
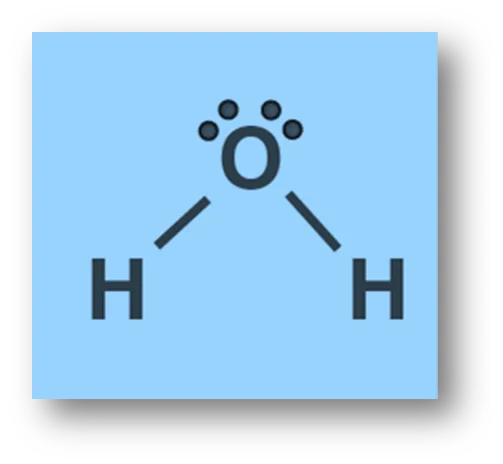
In water (H2O): Water has 2 bond pairs and 2 lone pairs on O- atom
Q : Distinguish Between a Sigma and a Pi Bond
| Property | Sigma (σ) Bond | Pi (π) Bond |
|---|---|---|
| 1. Formation | Formed by overlap of orbitals along internuclear axis | Formed by sideways overlap of orbitals |
| 2. Type of Orbitals | Can form by s–s, s–p, or p–p overlap | Formed by p–p or p–d overlap |
| 3. Electron Cloud | Electron cloud is symmetrical about internuclear axis; overlap is large → strong bond | Electron cloud lies above and below internuclear axis; overlap is small → weaker bond |
| 4. Rotation | Free rotation possible around σ-bond | Rotation restricted; rotation breaks π-bond |
| 5. Bond Length | Longer bond length | Shorter bond length |
| 6. Formation Order | Can form independently | Always forms after σ-bond formation |
Key Takeaway:
- Sigma bonds are stronger and allow free rotation, while pi bonds restrict rotation and are weaker.
Q : Explain the Formation of H2 Molecule on the Basis of Valence Bond Theory
Consider two hydrogen atoms A and B with electron eA and eB respectively. HA represents the nucleus of hydrogen atom ‘A’ and HB for hydrogen atom ‘B’. When the two hydrogen atoms approach each other, the following two forces come into existence:
(a) Attractive forces between (i) electron eA and nucleus HB (ii) electron eB and nucleus HA.
(b) Repulsive forces between (i) electron eA and electron eB (ii) nucleus HA and nucleus HB.
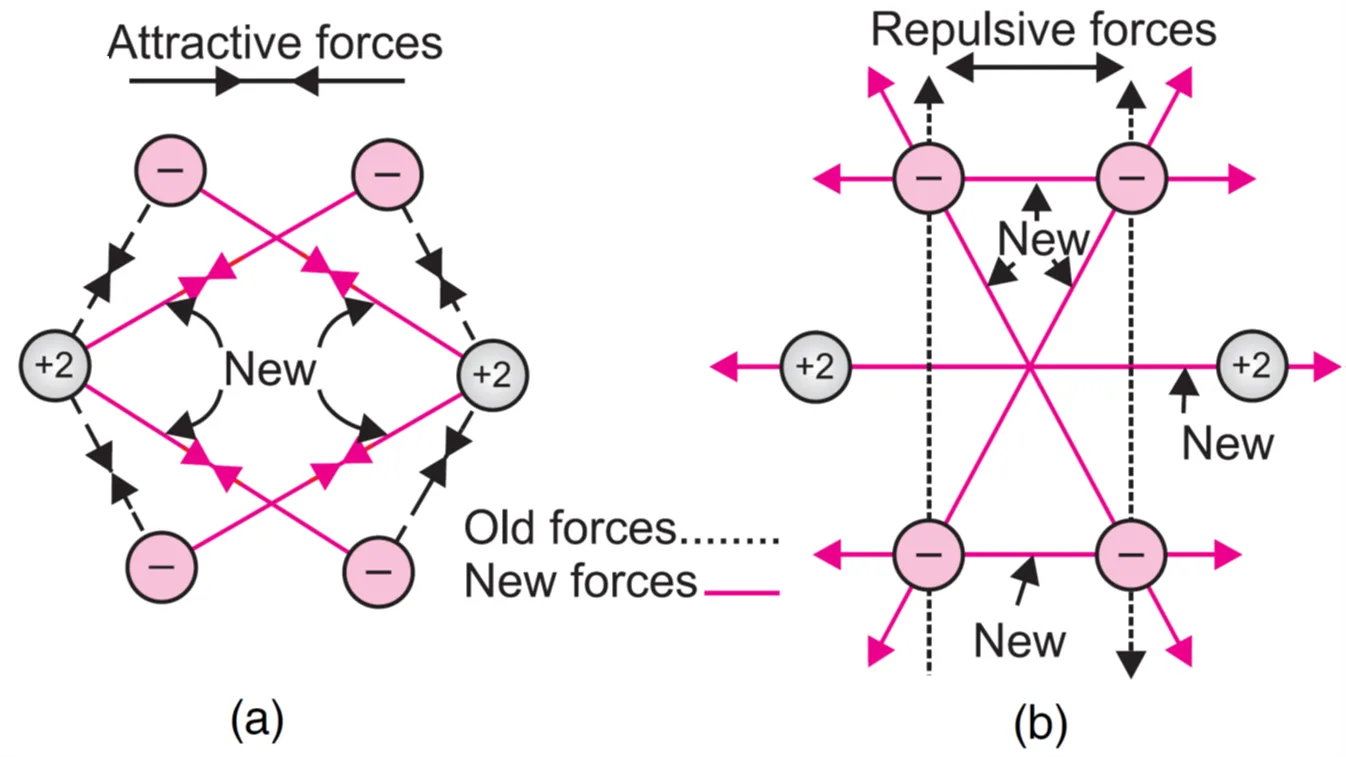
The attractive forces tend to bring the atom close to each other, whereas repulsive forces tend to push them apart.
Since the magnitude of attractive forces is greater than the repulsive forces, as a result, the energy of the system decreases and a molecule of hydrogen is formed.
Key Takeaway:
When these atoms approach each other, two types of forces operate:
- Attractive forces between:
- $e_A$ and nucleus $H_B$
- $e_B$ and nucleus $H_A$
- Repulsive forces between:
- $e_A$ and $e_B$
- $H_A$ and $H_B$
Attractive forces bring atoms closer, while repulsive forces push them apart.
Since attraction dominates, the potential energy decreases, forming a stable $H_2$ molecule.
- $H_2$ forms when net attraction exceeds repulsion, leading to lower energy and stability.
Q : Write the important conditions required for the linear combination of atomic orbitals to form molecular orbitals.
The main conditions for the Linear Combination of Atomic Orbitals (LCAO) method are:
- When two atomic orbitals combine they loose their original identity and form new orbitals which are termed as molecular orbitals (MOs).
- Only those atomic orbitals combine to form molecular orbitals which have comparable energies and proper orientation.
- The number of MOs formed equals the number of AOs combined.
- Two AOs form one bonding MO (lower energy) and one antibonding MO (higher energy).
- Filling of MOs follows Aufbau principle, Pauli’s exclusion principle, and Hund’s rule.
Key Takeaway:
- Only orbitals with similar energy and symmetry combine to form stable molecular orbitals.
Q : Use molecular orbital theory to explain why the Be2 molecule does not exist.
For beryllium ($Z=4$):
Atomic Electronic configuration: $$\text{Be: } 1s^2, 2s^2$$
Molecular orbital configuration: $$(σ1s)^2(σ^*1s)^2(σ2s)^2(σ^*2s)^2$$
Bond order:
$$
\text{B.O.} = \frac{N_b – N_a}{2} = \frac{4 – 4}{2} = 0
$$
Since bond order = 0, Be2 does not exist.
Key Takeaway:
- Bond order 0 → No bond formation, molecule does not exist.
Q : Compare the relative stability of the following species and indicate their magnetic properties: O2, O2+ ,O2– (superoxide), O22-(peroxide)
(i) Molecular Oxygen (O2)
The electronic configuration of $O_2$ is:
$$
O_2 = (σ2s)^2(σ^*2s)^2(σ2p_z)^2(π2p_x)^2(π2p_y)^2(π^*2p_x)^1(π^*2p_y)^1
$$
Number of bonding electrons ($N_b$) = 8
Number of antibonding electrons ($N_a$) = 4
Therefore,
$$
\text{Bond Order} = \frac{N_b – N_a}{2} = \frac{8 – 4}{2} = 2
$$
Since there are two unpaired electrons in the $π^*$ orbitals, $O_2$ is paramagnetic.
(ii) Oxygen Cation ($O_2^+$)
The electronic configuration of $O_2^+$ is:
$$
O_2^+ = (σ2s)^2(σ^*2s)^2(σ2p_z)^2(π2p_x)^2(π2p_y)^2(π^*2p_x)^1
$$
Number of bonding electrons ($N_b$) = 8
Number of antibonding electrons ($N_a$) = 3
Hence,
$$
\text{Bond Order} = \frac{8 – 3}{2} = 2.5
$$
$O_2^+$ has one unpaired electron, so it is paramagnetic.
It has higher bond order and stability than $O_2$.
(iii) Superoxide Ion ($O_2^-$)
The electronic configuration of $O_2^-$ is:
$$
O_2^- = (σ2s)^2(σ^*2s)^2(σ2p_z)^2(π2p_x)^2(π2p_y)^2(π^*2p_x)^2(π^*2p_y)^1
$$
Number of bonding electrons ($N_b$) = 8
Number of antibonding electrons ($N_a$) = 5
So,
$$
\text{Bond Order} = \frac{8 – 5}{2} = 1.5
$$
It contains one unpaired electron, hence $O_2^-$ is paramagnetic, but less stable than $O_2$.
(iv) Peroxide Ion ($O_2^{2-}$)
The electronic configuration of $O_2^{2-}$ is:
$$
O_2^{2-} = (σ2s)^2(σ^*2s)^2(σ2p_z)^2(π2p_x)^2(π2p_y)^2(π^*2p_x)^2(π^*2p_y)^2
$$
Number of bonding electrons ($N_b$) = 8
Number of antibonding electrons ($N_a$) = 6
Thus,
$$
\text{Bond Order} = \frac{8 – 6}{2} = 1
$$
There are no unpaired electrons, so $O_2^{2-}$ is diamagnetic and least stable among these species.
Final Comparison
The order of bond order (and hence stability) is:
$$
O_2^+ > O_2 > O_2^- > O_2^{2-}
$$
The magnetic nature follows:
- $O_2^+$ → Paramagnetic (1 unpaired electron)
- $O_2$ → Paramagnetic (2 unpaired electrons)
- $O_2^-$ → Paramagnetic (1 unpaired electron)
- $O_2^{2-}$ → Diamagnetic (no unpaired electrons)
Key Takeaways:
- Bond order decreases from $O_2^+$ to $O_2^{2-}$.
- Greater bond order → more stability.
- Presence of unpaired electrons → paramagnetism.
Q : Write the significance of a plus and a minus sign shown in representing the orbitals.
Orbitals are represented by wave functions (ψ).
- ‘+’ sign → positive phase of wave function.
- ‘–’ sign → negative phase of wave function.
Key Takeaway:
- The signs indicate phase of the wave function, important in bonding and interference.
Q : Describe the hybridisation of PCl5. Why are the axial bonds longer as compared to equatorial bonds ?
In phosphorus pentachloride (PCl5), phosphorus undergoes sp3d hybridization because one of the 3s electron of ‘p’ gets promoted to 3d orbital giving the electronic configuration :
$$
3s^2 3p^3 \rightarrow 3s^1 3p^3 3d^1
$$
In PCl5, the central atom, P has five valence electrons. It forms five bond pairs with five Cl-atoms to form a molecule of PCl5. Since there are five electron pairs around the central phosphorus atom, it has trigonal bipyramidal geometry.
In this geometry, all the bond angles are not equal. Three electron pairs are in the same plane at an angle of 120o, while the other two bond pairs are perpendicular to the plane, both making an angle of 90o with the plane. Thus, in this arrangement three bond angles are of 120o each and two are of 90o each.
In this geometry, all five P–Cl bonds are not equal. The three bonds lying in the trigonal plane are called equatorial bonds. Of the remaining two bonds, one lies above and the other below the equatorial plane, both making an angle of 90o with the plane. These bonds are called axial bonds.
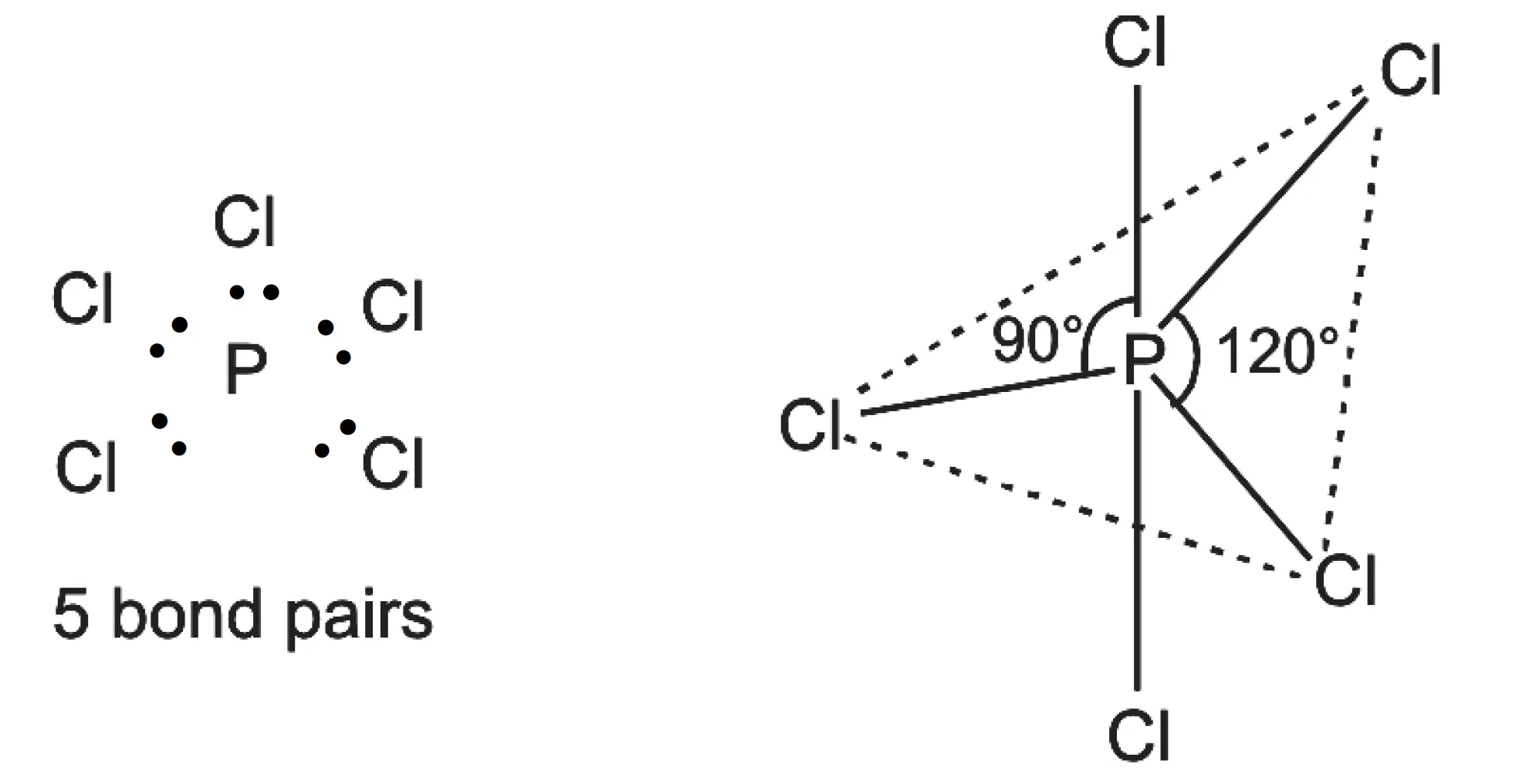
pairs around P-atom
It has been observed that axial bonds are slightly longer than equatorial bonds in this geometry.
The larger bond length of axial bonds than equatorial bonds can be explained in terms of the repulsive forces between electron pairs due to different bond angles.
Let us count the repulsive interactions of an axial and an equatorial electron pair:
- The electron pair of an axial bond (say 1) is repelled by three electron pairs (of bonds 2, 3, and 4) at 90o and one (bond 5) at 180o.
- The electron pair of an equatorial bond (say 2) is repelled by two electron pairs (1 and 5) at 90o and two (3 and 4) at 120o.
Since repulsion between electron pairs decreases with increasing angle, the repulsions at 120o and 180o may be neglected compared to those at 90o.
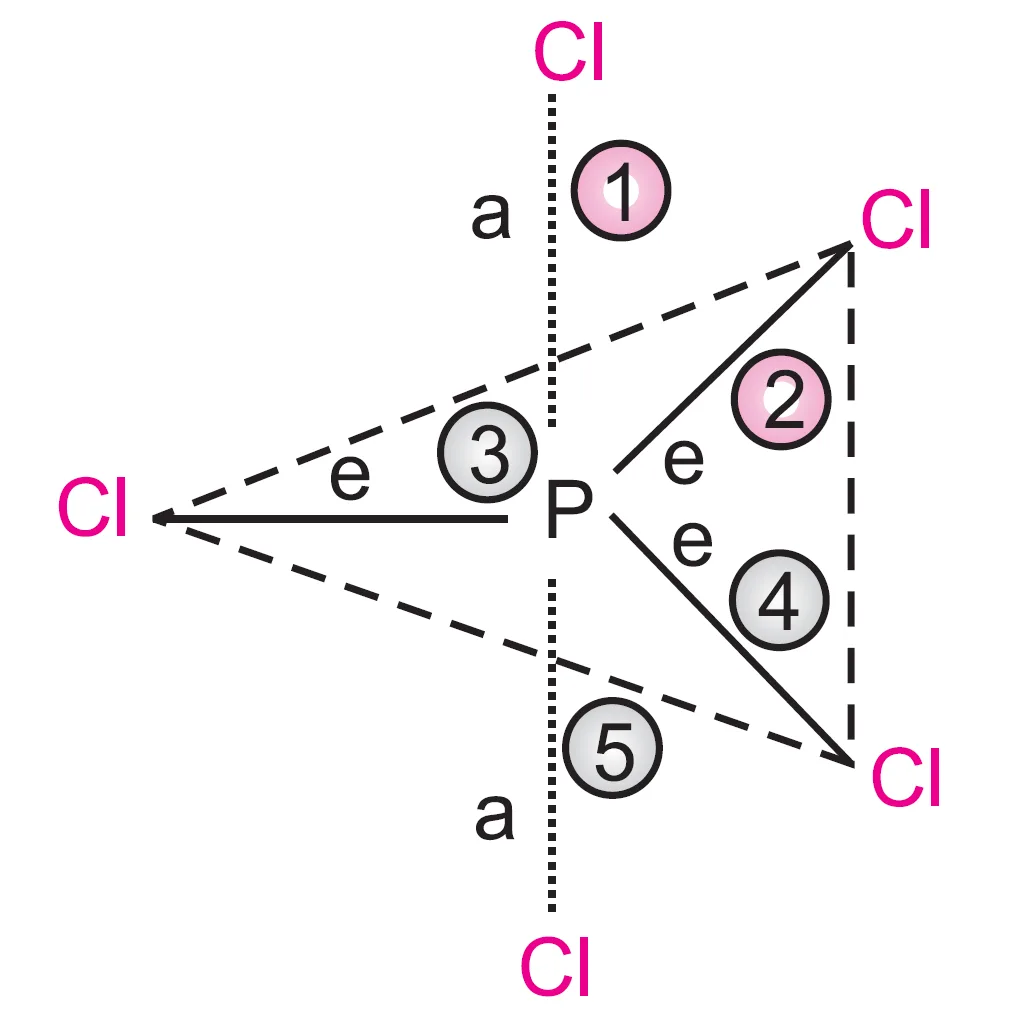
Thus, considering only the 90o repulsions:
- Each axial bond is repelled by three bond pairs.
- Each equatorial bond is repelled by two bond pairs.
Hence, the axial bond pair faces greater repulsion, making the axial bond slightly longer than the equatorial bond.
It may be noted that the structure of PCl5 molecule is unsymmetrical. As a result, it is less stable and is therefore, highly reactive. Therefore PCl5 is dissociate to PCl3.
Q : Define hydrogen bond. Is it weaker or stronger than the van der Waals forces ?
When hydrogen is bonded to highly electronegative atoms (F, O, N), the bond becomes polar:
$$
\text{H}^\delta+ – \text{A}^\delta-
$$
This partial charge separation leads to intermolecular attraction called hydrogen bonding.

A hydrogen bond is an intermolecular (sometimes intramolecular) force that occurs when a hydrogen atom is covalently bonded to a highly electronegative atom such as fluorine (F), oxygen (O), or nitrogen (N), and this hydrogen is attracted to another nearby electronegative atom.
1. Nature of the Hydrogen Bond
- In a molecule like H–F, H–O, or H–N, the electronegative atom pulls the shared electron pair closer to itself.
- This leaves the hydrogen atom partially positive ($\delta^+$) and the electronegative atom partially negative ($\delta^-$).
- The electrostatic attraction between the $\delta^+$ hydrogen and the $\delta^-$ atom of a neighboring molecule forms a hydrogen bond.
Example:
$$
\text{H–F···H–F···H–F}
$$
Here, the dots (···) represent hydrogen bonds.
Hydrogen bond is stronger than van der Waals forces, but weaker than covalent bonds.
Why is Hydrogen Bond Stronger than van der Waals Forces but Weaker than Covalent Bonds?
| Type of Bond | Approximate Strength (kJ/mol) | Nature of Interaction |
|---|---|---|
| Covalent bond | 200–400 | Strong intramolecular sharing of electrons |
| Hydrogen bond | 10–40 | Moderate intermolecular electrostatic attraction |
| van der Waals forces | < 10 | Weak, temporary dipole-induced interactions |
(a) Hydrogen Bonds Stronger than van der Waals Forces
- van der Waals forces (London dispersion or dipole–dipole interactions) arise due to temporary or induced dipoles, which are weak and short-lived.
- Hydrogen bonds, however, involve a permanent dipole between highly electronegative atoms and hydrogen.
- Therefore, the electrostatic attraction in hydrogen bonds is much stronger than the weak fluctuations in van der Waals interactions.
(b) Hydrogen Bonds Weaker than Covalent Bonds
- In a covalent bond, atoms share electrons, forming a true chemical bond with significant electron density between nuclei.
- In contrast, a hydrogen bond does not involve electron sharing but merely an electrostatic attraction between dipoles.
- Thus, hydrogen bonds are intermolecular and partially electrostatic, making them weaker than covalent bonds.
Examples
- Hydrogen Fluoride (HF): Strong hydrogen bonding causes high boiling point.
$$ \text{H–F···H–F···H–F} $$ - Water (H₂O): Each water molecule forms four hydrogen bonds, leading to its high cohesion and unusual density in the solid state (ice).
$$ \text{H–O···H–O···H–O} $$
Key Takeaways
- Hydrogen bonds are stronger than van der Waals forces because they involve permanent dipole–dipole attraction.
- They are weaker than covalent bonds since no electron sharing occurs.
- Their strength range (10–40 kJ/mol) places them intermediate between these two types of forces.
- Hydrogen bonding significantly affects boiling points, melting points, viscosity, and solubility of compounds.
- Hydrogen bonds are directional and stronger than van der Waals, crucial in water and biomolecules.
What Is Bond Order? Calculate Bond Order of N2, O2, O2+, and O2–.
Bond Order
Bond Order (B.O.) is defined as half the difference between the number of bonding electrons ($N_b$) and antibonding electrons ($N_a$) in a molecule.
$$
\text{Bond Order (B.O.)} = \frac{1}{2}(N_b – N_a)
$$
Key Point:
- Higher bond order → Stronger bond → Shorter bond length.
- If bond order = 0, the molecule does not exist.
Molecular Orbital (MO) Configurations
For homonuclear diatomic molecules, the molecular orbital filling order (up to oxygen) is:
$$
O_2 = (σ1s)^2(σ^*1s)^2(σ2s)^2(σ^*2s)^2(σ2p_z)^2(π2p_x)^2(π2p_y)^2(π^*2p_x)^1(π^*2p_y)^1
$$
(a) Nitrogen Molecule (N2)
Atomic number of N = 7, so
Total electrons in N2 = 14.
Electronic Configuration in MOs:
$$
N_2 = (σ1s)^2(σ^*1s)^2(σ2s)^2(σ^*2s)^2(σ2p_z)^2(π2p_x)^2(π2p_y)^2
$$
- Bonding electrons ($N_b$) = 10
- Antibonding electrons ($N_a$) = 4
$$
\text{B.O.} = \frac{1}{2}(10 – 4) = 3
$$
✅ Bond Order = 3 (Triple bond)
→ Very stable and diamagnetic (no unpaired electrons).
(b) Oxygen Molecule (O2)
Atomic number of O = 8, so
Total electrons in O₂ = 16.
Electronic Configuration in MOs:
$$
O_2 = (σ1s)^2(σ^*1s)^2(σ2s)^2(σ^*2s)^2(σ2p_z)^2(π2p_x)^2(π2p_y)^2(π^*2p_x)^1(π^*2p_y)^1
$$
- $N_b = 10$, $N_a = 6$
$$
\text{B.O.} = \frac{1}{2}(10 – 6) = 2
$$
✅ Bond Order = 2 (Double bond)
→ Paramagnetic due to 2 unpaired electrons in $\pi^*$ orbitals.
(c) Oxygen Cation (O2+)
One electron is removed from O2’s antibonding $\pi^*$ orbital.
- $N_b = 10$, $N_a = 5$
$$
\text{B.O.} = \frac{1}{2}(10 – 5) = 2.5
$$
✅ Bond Order = 2.5
→ Stronger and shorter bond than O₂.
→ Paramagnetic (1 unpaired electron).
(d) Oxygen Anion (O2–)
One extra electron enters an antibonding $\pi^*$ orbital.
- $N_b = 10$, $N_a = 7$
$$
\text{B.O.} = \frac{1}{2}(10 – 7) = 1.5
$$
✅ Bond Order = 1.5
→ Weaker and longer bond than O₂.
→ Paramagnetic (1 unpaired electron).
Summary of Bond Order and Magnetic Nature
| Species | $N_b$ | $N_a$ | Bond Order | Magnetic Nature |
|---|---|---|---|---|
| N2 | 10 | 4 | 3.0 | Diamagnetic |
| O2+ | 8 | 3 | 2.5 | Paramagnetic |
| O2 | 8 | 4 | 2.0 | Paramagnetic |
| O2– | 8 | 5 | 1.5 | Paramagnetic |
Key Takeaways
- Bond order decreases in the sequence:
$$ O_2^+ > O_2 > O_2^- $$ - Higher bond order → Greater stability → Shorter bond length.
- Paramagnetism arises due to unpaired electrons in antibonding orbitals.
🔍 Summary
Understanding chemical bonding, bond pairs and lone pairs, sigma and pi bonds, and molecular orbital theory is crucial in Class 11 Chemistry.
Concepts like hybridization (sp³, sp³d), hydrogen bonding, and bond order explain molecular shapes, stability, and magnetism.


