Anand Classes provides a clear and detailed explanation of the Molecular Orbital Theory (MOT), focusing on the formation of bonding and antibonding molecular orbitals. Students will understand how atomic orbitals combine to form molecular orbitals, the concept of bond order, magnetic properties, and stability of molecules. This topic is crucial for mastering modern chemical bonding concepts and is supported with diagrams, solved examples, MCQs, Q&A, Assertion-Reason, and Case Study questions for Class 11, Class 12, JEE, and NEET chemistry preparation. Click the print button to download study material and notes.
What is Molecular Orbital Theory (MOT) ?
Molecular orbital theory was developed by F. Hund and R.S. Mulliken in 1932.
The basic idea of molecular orbital theory is that atomic orbitals of individual atoms combine to form molecular orbitals. The electrons in molecules are present in the molecular orbitals which are associated with several nuclei.
These molecular orbitals are filled in the same way as the atomic orbitals in atoms are filled.
What are the Salient Features of Molecular Orbital Theory?
The salient features of the molecular orbital theory are:
- Just like an atom, a molecule has orbitals of definite energy levels. Like electrons of atoms are present in atomic orbitals, electrons of a molecule are present in different molecular orbitals.
- Molecular orbitals are formed by the combination of atomic orbitals of proper symmetry and comparable energies.
- An electron in an atomic orbital is under the influence of only one nucleus. However, an electron in a molecular orbital is under the influence of two or more nuclei depending upon the number of atoms present in the molecule.
- Thus, an atomic orbital is monocentric, while a molecular orbital is polycentric.
- Just as the electron probability distribution around a nucleus in an atom is given by an atomic orbital, the electron probability distribution around a group of nuclei in a molecule is given by a molecular orbital.
- The number of molecular orbitals formed = number of combining atomic orbitals.
- When two atomic orbitals combine, they form two molecular orbitals:
- Bonding molecular orbital (BMO)
- Antibonding molecular orbital (ABMO)
- When two atomic orbitals combine, they form two molecular orbitals:
- The bonding MO has lower energy and greater stability, whereas the corresponding antibonding MO has higher energy and lesser stability.
- The molecular orbitals are filled in the same way as atomic orbitals, following:
- Aufbau principle
- Pauli exclusion principle
- Hund’s rule
How are Molecular Orbitals Formed?
Molecular orbitals are formed by the combination of atomic orbitals of bonded atoms.
According to wave mechanics, the atomic orbitals can be expressed by wave functions ($\psi$’s). These wave functions represent the amplitude of the electron waves, obtained from the Schrödinger wave equation.
For molecules, solving Schrödinger equation is very complex. To overcome this, scientists developed an approximate method called the Linear Combination of Atomic Orbitals (LCAO) method.
What is the LCAO Method of Molecular Orbital Formation?
According to the LCAO method, molecular orbitals are formed by linear combination (addition or subtraction) of atomic orbitals of the atoms.
Example: Hydrogen molecule (H2)
- Hydrogen molecule consists of two atoms A and B.
- Each atom has a 1s-orbital.
- The orbitals are represented by $\psi_A$ and $\psi_B$.
When these orbitals come close, they combine to form molecular orbitals:
$$\psi_{MO} = \psi_A \pm \psi_B$$
This results in two types of molecular orbitals:
- Bonding Molecular Orbital (BMO)
$$\psi_{MO} = \psi_A + \psi_B$$
or $$\sigma = \psi_A + \psi_B$$ - Antibonding Molecular Orbital (ABMO)
$$\psi*_{MO} = \psi_A – \psi_B$$
or $$\sigma* = \psi_A – \psi_B$$
What is the Physical Picture of Bonding and Antibonding Molecular Orbitals?
To illustrate this, we may take the combination of 1s-orbital of one hydrogen atom with 1s-orbital of second hydrogen atom to form two molecular orbitals in hydrogen molecule.
There are two ways of combining atomic orbitals. The molecular orbital formed by the addition of overlapping of two 1s-orbitals is shown in Figure.

It is clear from the figure that the region between the two nuclei where the two 1s-atomic orbitals overlap has high electron density. Therefore, repulsion between the nuclei is very less. Such a molecular orbital is called bonding molecular orbital.
The molecular orbital formed by the subtraction of overlapping of two 1s-orbitals is shown in Figure.

It is clear from the figure that the electron density in between the two nuclei is practically zero and most of the electron density is located away from the space between the two nuclei. This is because, the electron probability densities of two atomic orbitals get cancelled in the centre (by subtraction) so that there is no probability of finding the electron in the region of overlap i.e. between the nuclei. In fact, there is a nodal plane (on which the electron density is zero) between the nuclei and hence the repulsion between the nuclei is high. This situation does not favour the bond formation. Such an orbital is called anti-bonding molecular orbital.
- When two 1s-orbitals combine in hydrogen:
- Bonding Orbital ($\sigma_{1s}$)
- Electron density between nuclei is high.
- Repulsion between nuclei is low.
- Orbital is symmetrical about the molecular axis.
- Represented as $\sigma_{1s}$.
- Antibonding Orbital ($\sigma^*_{1s}$)
- Electron density between nuclei is zero.
- A nodal plane forms where electron density cancels out.
- Repulsion between nuclei is high, bond formation is not favored.
- Represented as $\sigma^*_{1s}$.
What are the Differences Between Atomic Orbitals and Molecular Orbitals?
| Atomic Orbital | Molecular Orbital |
|---|---|
| Electron is under the influence of one nucleus. | Electron is under the influence of two or more nuclei. |
| Inherent property of an atom. | Formed by combination of atomic orbitals. |
| Have simple shapes. | Have complex shapes. |
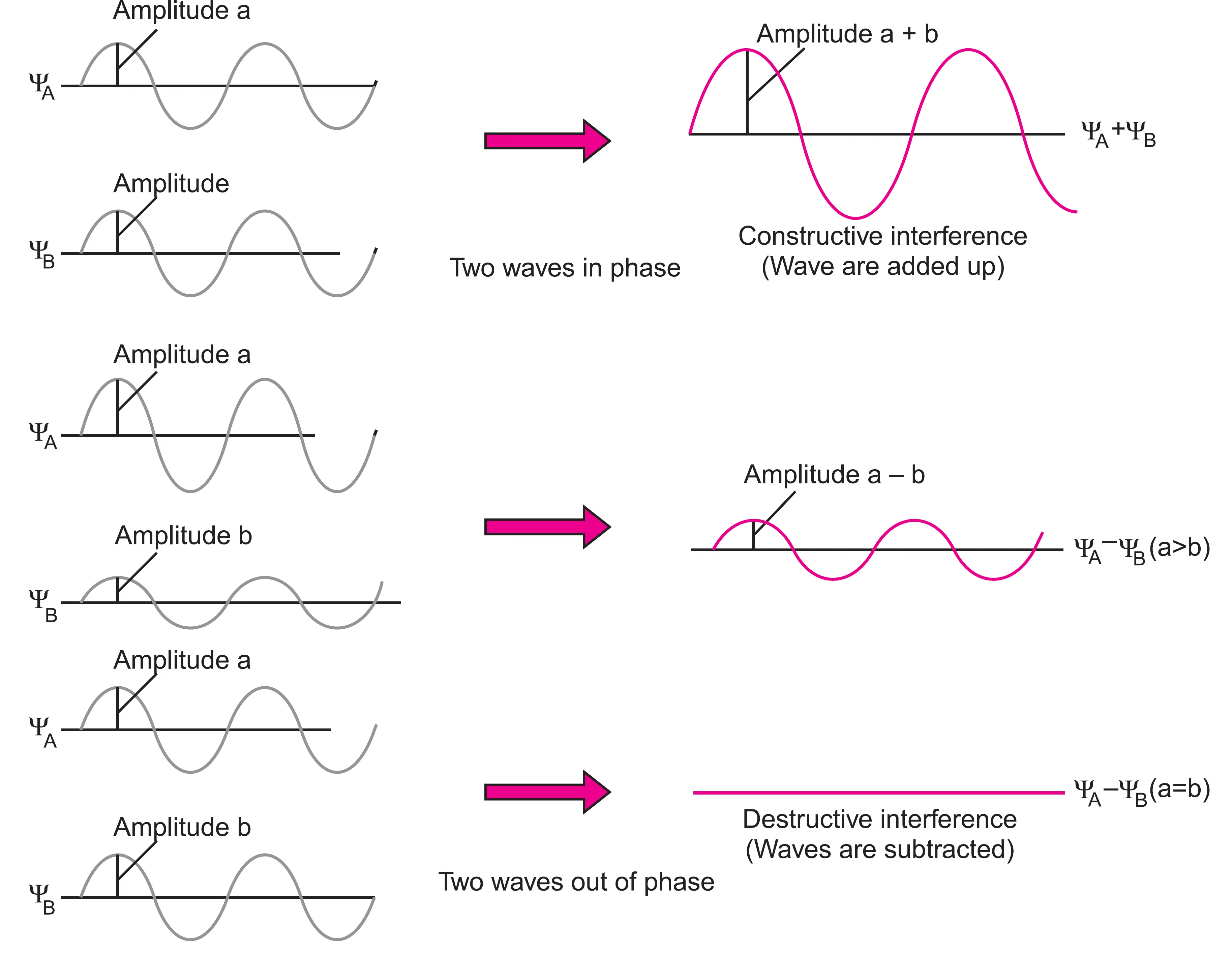
How is Bonding Explained Using Wave Interference?
The formation of bonding and antibonding molecular orbitals can be explained in terms of wave interference:
- Constructive Interference (Additive effect)
- Two waves are in phase.
- Amplitudes add up → electron density increases between nuclei.
- Results in Bonding Molecular Orbital (BMO).
- Destructive Interference (Subtractive effect)
- Two waves are out of phase.
- Amplitudes cancel out → electron density decreases between nuclei.
- A nodal plane forms.
- Results in Antibonding Molecular Orbital (ABMO).
How Can Probability Density Be Explained in Bonding and Antibonding Orbitals?
The probability density is given by the square of wave function ($\psi^2$).
- For Bonding MO:
$$\psi = \psi_A + \psi_B$$
$$\psi^2 = (\psi_A + \psi_B)^2 = \psi_A^2 + \psi_B^2 + 2\psi_A \psi_B$$ Probability is greater than individual atoms by an amount $2\psi_A \psi_B$.
Therefore, the probability of finding electrons in the bonding MO is greater than in either of atomic orbitals ($\psi_A \; or \; \psi_B$). - For Antibonding MO:
$$\psi^* = \psi_A – \psi_B$$
$$\psi^{*2} = (\psi_A – \psi_B)^2 = \psi_A^2 + \psi_B^2 – 2\psi_A \psi_B$$ Probability is less than individual atoms by an amount $2\psi_A \psi_B$.
Therefore, the probability of finding the electrons in antibonding MO is less than that in either of the atomic orbitals ($\psi_A \; or \; \psi_B$).
What is the Significance of + and – Signs in Wave Functions?
- ‘+’ and ‘–’ signs in wave functions correspond to the phase of electron waves (crests and troughs), not electric charges.
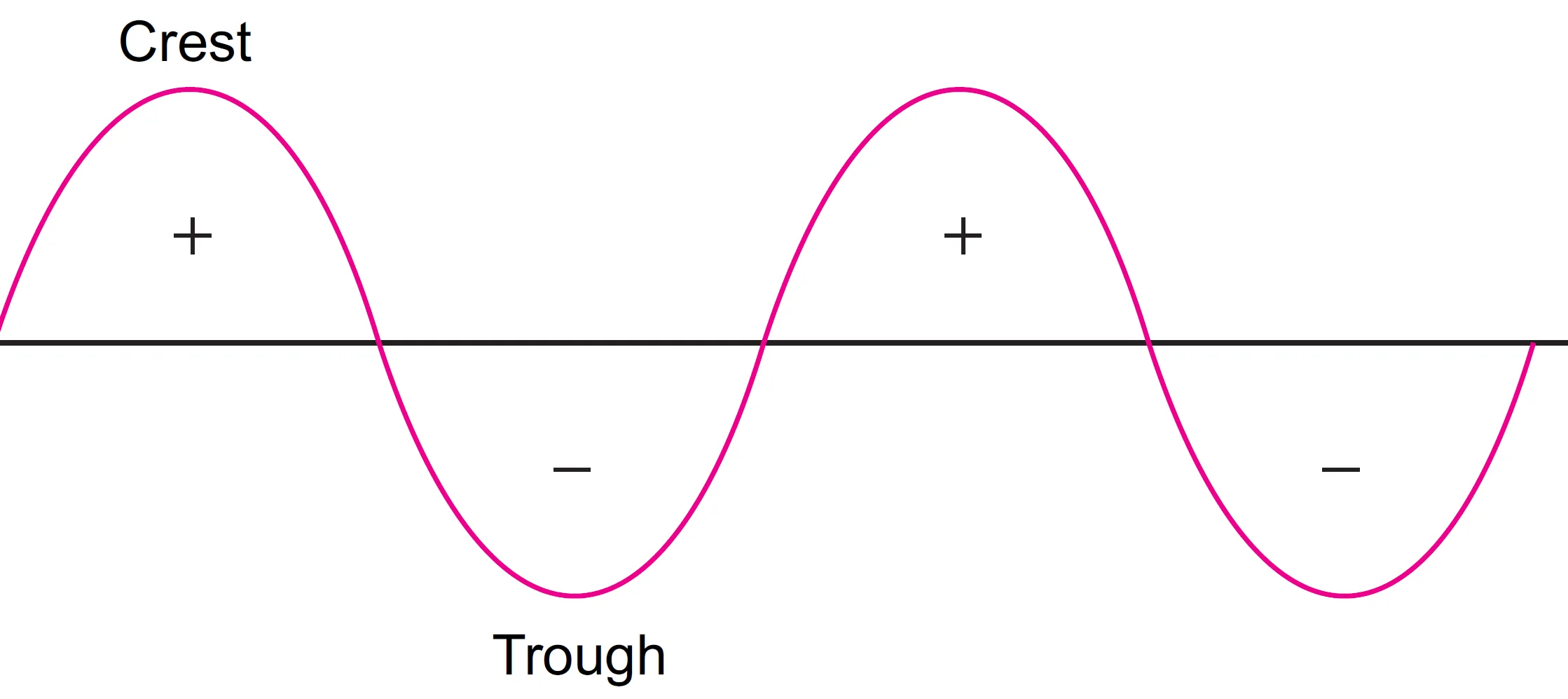
- Bonding MO → formed by combining (+) with (+) or (–) with (–) lobes.
- Antibonding MO → formed by combining (+) with (–) lobes.
To understand the overlapping of two bonding orbitals, it is necessary to give + or – signs of wave functions. It may be remembered that s-orbitals are spherically symmetrical and are +ve in all directions while the p-orbitals consisting of two lobes have one lobe with + ve sign and the other lobe with – ve sign.
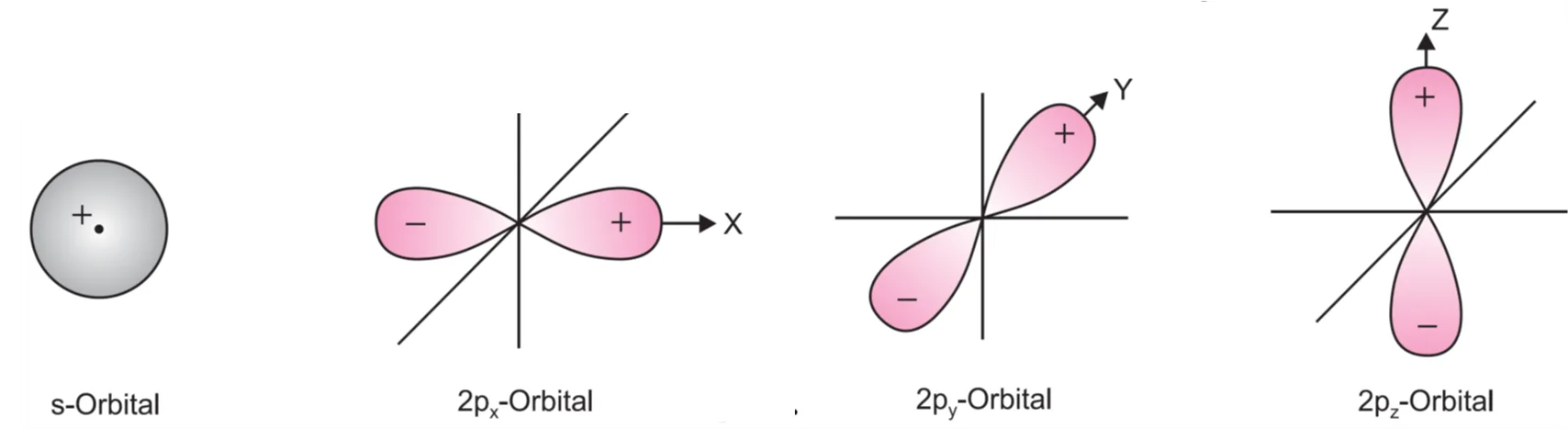
During overlapping or combination of atomic orbitals, only + + or – – lobes can combine. No combination is possible between + and – lobes.
📘 Practice Questions on Molecular Orbital Theory
🔹 Short Answer Conceptual Types (SAT)
Q1. Who developed Molecular Orbital Theory and in which year?
Answer: F. Hund and R.S. Mulliken in 1932.
Q2. What is the main difference between atomic orbitals and molecular orbitals?
Answer:
- Atomic orbital is monocentric (influence of one nucleus).
- Molecular orbital is polycentric (influence of two or more nuclei).
Q3. Define Bonding Molecular Orbital (BMO)
Answer: A bonding molecular orbital is formed by constructive interference (addition) of wave functions of atomic orbitals, resulting in lower energy, greater stability, and high electron density between nuclei.
Q4. Why is antibonding molecular orbital less stable?
Answer: Because electron density between nuclei is reduced (destructive interference), a nodal plane appears, and repulsion between nuclei increases.
Q5. What is the relation between number of atomic orbitals and molecular orbitals formed?
Answer: The number of molecular orbitals formed = number of atomic orbitals combined.
🔹 Multiple Choice Questions (MCQs)
Q1. Which of the following is true for bonding molecular orbital?
(a) Higher energy, less stability
(b) Lower energy, greater stability
(c) Same energy as atomic orbital
(d) No effect on stability
Answer: (b) Lower energy, greater stability
Explanation: Bonding MO is formed by constructive overlap, increasing electron density between nuclei, reducing repulsion.
Q2. The correct relation for formation of molecular orbital is:
(a) $\psi_{MO} = \psi_A \times \psi_B$
(b) $\psi_{MO} = \psi_A \pm \psi_B$
(c) $\psi_{MO} = \psi_A^2 + \psi_B^2$
(d) $\psi_{MO} = \psi_A – \psi_B^2$
Answer: (b) $\psi_{MO} = \psi_A \pm \psi_B$
Explanation: Molecular orbitals are formed by linear combination (addition/subtraction) of wave functions.
Q3. Which molecular orbital is represented as $\sigma^*1s$?
(a) Bonding MO from 1s-orbitals
(b) Antibonding MO from 1s-orbitals
(c) Bonding MO from 2p-orbitals
(d) Antibonding MO from 2p-orbitals
Answer: (b) Antibonding MO from 1s-orbitals
Explanation: The asterisk (*) denotes antibonding orbital.
Q4. Which rule is not applicable to filling of molecular orbitals?
(a) Aufbau principle
(b) Pauli exclusion principle
(c) Hund’s rule
(d) Octet rule
Answer: (d) Octet rule
Explanation: Octet rule is not a quantum mechanical rule.
Q5. If bond order = 0, the molecule is:
(a) Stable
(b) Highly stable
(c) Unstable
(d) Resonating
Answer: (c) Unstable
Explanation: Bond order = $frac{N_b – N_a}{2}$. If 0, no net bond exists.
🔹 Assertion-Reason Type Questions
Q1.
Assertion (A): Bonding molecular orbital has lower energy than atomic orbitals.
Reason (R): Electron density between the nuclei increases in bonding MO.
- (a) Both A and R are true, and R is the correct explanation.
- (b) Both A and R are true, but R is not the correct explanation.
- (c) A is true, R is false.
- (d) A is false, R is true.
Answer: (a) Both A and R are true, and R is the correct explanation.
Q2.
Assertion (A): In antibonding MO, a nodal plane is present between nuclei.
Reason (R): This occurs due to destructive interference of electron waves.
- (a) Both A and R are true, and R is the correct explanation.
- (b) Both A and R are true, but R is not the correct explanation.
- (c) A is true, R is false.
- (d) A is false, R is true.
Answer: (a) Both A and R are true, and R is the correct explanation.
Q3.
Assertion (A): Bonding molecular orbital is polycentric.
Reason (R): Bonding molecular orbital is influenced by only one nucleus.
Answer: (c) A is true, R is false.
Explanation: MO is polycentric because it is influenced by two or more nuclei, not one.
🔹 Case Study Question
Read the passage and answer the questions:
Molecular Orbital Theory explains that when two atomic orbitals combine, they form two molecular orbitals — one bonding and one antibonding. The bonding MO has lower energy and provides stability to the molecule, while antibonding MO has higher energy and destabilizes the molecule. For H₂, bond order = 1, so it is stable. But for He₂, bond order = 0, so it is unstable.
Q1. How many molecular orbitals are formed when two atomic orbitals combine?
Answer: Two (Bonding MO and Antibonding MO).
Q2. Why is H₂ stable but He₂ unstable?
Answer:
- For H₂: Bond order = $\frac{2-0}{2} = 1$ → stable.
- For He₂: Bond order = $\frac{2-2}{2} = 0$ → unstable.
Q3. Which has greater energy: bonding MO or antibonding MO?
Answer: Antibonding MO.
Q4. What is the role of bond order in predicting stability?
Answer: If bond order > 0 → stable molecule, if bond order = 0 → unstable molecule.



