Anand Classes provides NCERT Solutions for Class 11 Maths Chapter 10 – Conic Sections (Miscellaneous Exercise) as per the latest NCERT and CBSE syllabus (2025–2026). This exercise includes a comprehensive mix of questions covering all types of conic sections — Circle, Parabola, Ellipse, and Hyperbola. Students can practice application-based problems involving standard equations, latus rectum, eccentricity, foci, directrix, and geometrical properties of different conic curves. Each solution is explained step-by-step to help students master coordinate geometry and prepare efficiently for CBSE Board Exams, JEE Main, JEE Advanced, NDA, and CUET. Click the print button to download study material and notes.
NCERT Question.5 : A rod of length $12\ \text{cm}$ moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point $P$ on the rod which is $3\ \text{cm}$ from the end in contact with the $x$–axis.
Solution :
Let $AB$ be the rod of length $12\ \text{cm}$ and $P(x, y)$ be the point on it such that $AP = 3\ \text{cm}$ (given).
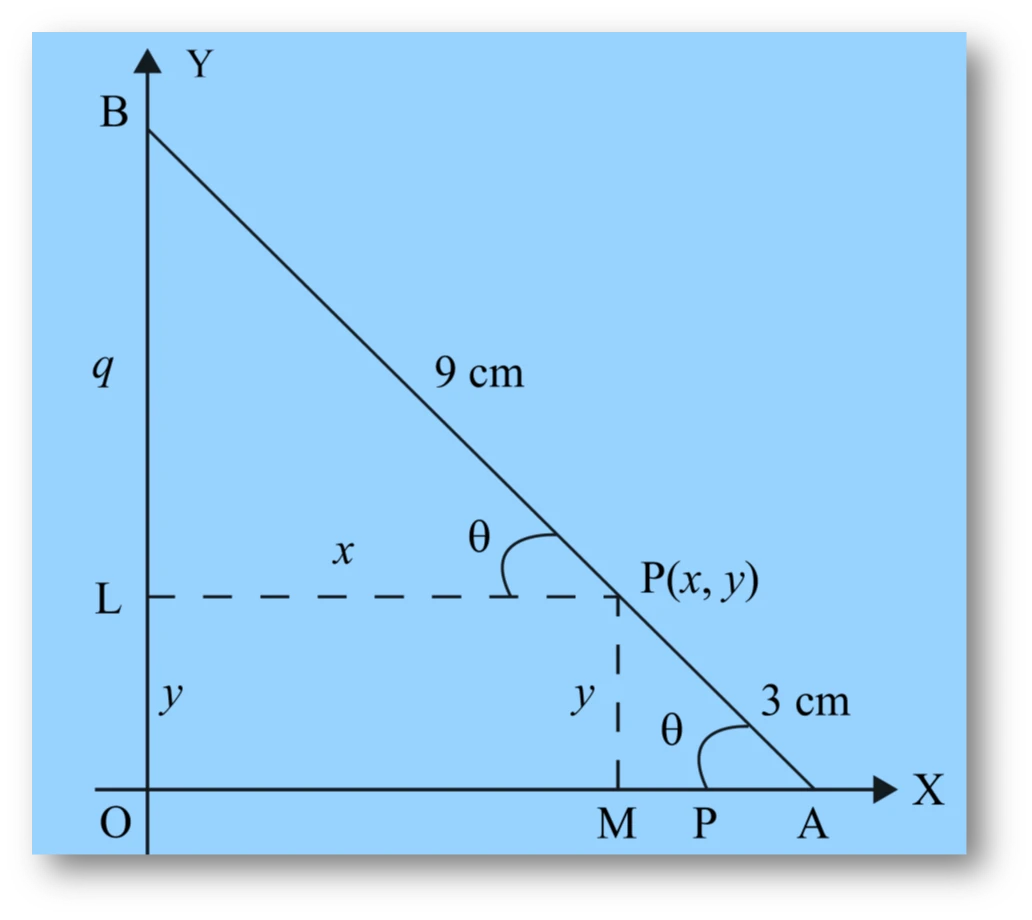
Therefore,
$$PB = AB – AP = 12 – 3 = 9\ \text{cm}.$$
From $P$, draw $PL$ and $PM$ perpendiculars on the $y$-axis and $x$-axis respectively.
Hence,
$$PL = x \quad \text{and} \quad PM = y.$$
Let $\angle OAB = \theta.$
Then $\angle LPB = \theta$ (corresponding angles).
In right-angled $\triangle AMP$,
$$\sin \theta = \frac{MP}{AP} = \frac{y}{3} \quad \text{…(i)}$$
In right-angled $\triangle PLB$,
$$\cos \theta = \frac{PL}{PB} = \frac{x}{9} \quad \text{…(ii)}$$
Using the trigonometric identity $sin^2 theta + cos^2 theta = 1$, we get
$$\left( \frac{y}{3} \right)^2 + \left( \frac{x}{9} \right)^2 = 1$$
or
$$\frac{x^2}{81} + \frac{y^2}{9} = 1.$$
Final Answer
The required locus of point $P$ is
$$\boxed{\frac{x^2}{81} + \frac{y^2}{9} = 1}$$
Hence, the locus of $P$ is an ellipse.
NCERT Question.6 : Find the area of the triangle formed by the lines joining the vertex of the parabola $x^2 = 12y$ to the ends of its latus rectum.
Solution :
The given parabola is
$$x^2 = 12y$$
Comparing with the standard form $x^2 = 4ay$, we get
$$4a = 12 \Rightarrow a = 3$$
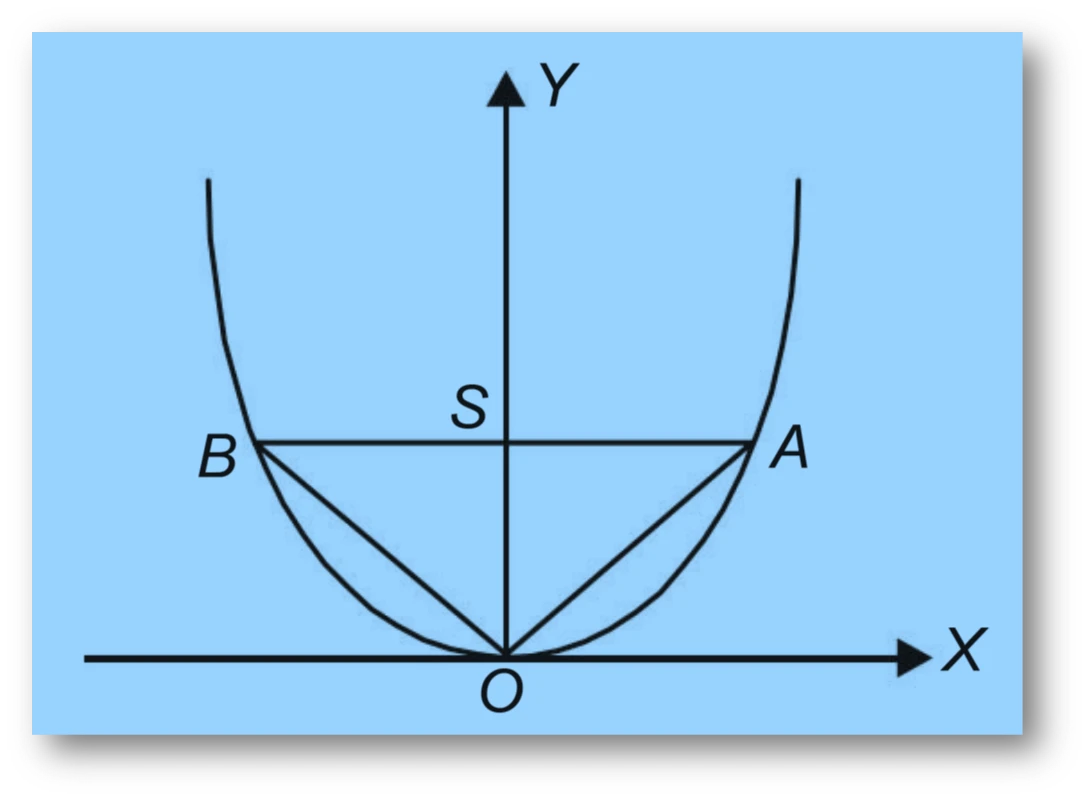
Let $S$ be the focus, $O$ be the vertex, and $AB$ be the latus rectum which is perpendicular to the axis $OS$.
The length of the latus rectum is
$$AB = 4a = 12$$
The coordinates of the focus are
$$S(0, a) = (0, 3)$$
Hence,
$$OS = 3$$
The area of the $\triangle OAB$ is given by
$$\text{Area of } \triangle OAB = \frac{1}{2} \times AB \times OS$$
Substituting the values,
$$\text{Area} = \frac{1}{2} \times 12 \times 3 = 18$$
$$
\boxed{\text{Area of the triangle } OAB = 18 \text{ square units.}}
$$
NCERT Question.7 : A man running a race-course notes that the sum of the distances from the two flag posts to him is always 10 m, and the distance between the flag posts is 8 m. Find the equation of the path traced by the man.
Solution :
Let $S$ and $S’$ be the two flag posts and $P$ the position of the man at any instant.
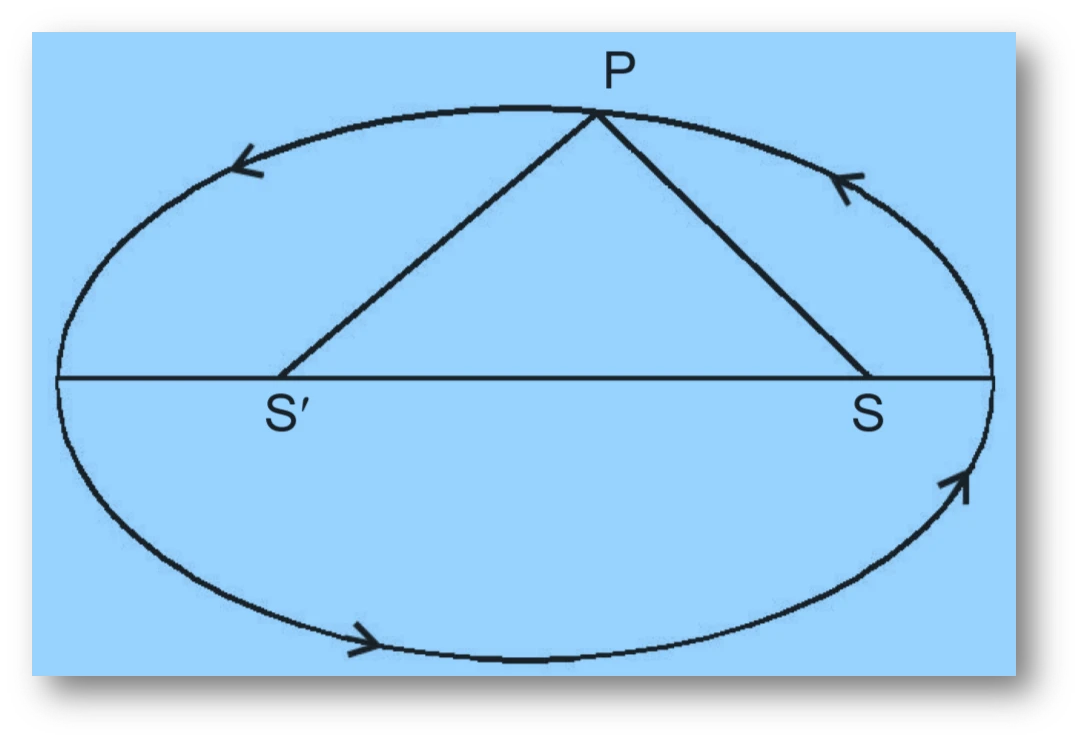
Since $PS + PS’ = 10$ (given), by definition of an ellipse, the path traced by the man is an ellipse with foci at the two flag posts and major axis of length 10.
Let the equation of the ellipse be
$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad …(i)$$
The length of the major axis is $2a$, so
$$2a = 10 \Rightarrow a = 5$$
The distance between the foci is $SS’ = 2c = 8 \Rightarrow c = 4$
Using the relation $c^2 = a^2 – b^2$, we get
$$4^2 = 5^2 – b^2 \Rightarrow b^2 = 25 – 16 = 9$$
Substituting $a^2 = 25$ and $b^2 = 9$ into equation (i), the equation of the path is
$$\frac{x^2}{25} + \frac{y^2}{9} = 1$$
$$
\boxed{\frac{x^2}{25} + \frac{y^2}{9} = 1}
$$
NCERT Question.8 : An equilateral triangle is inscribed in the parabola $y^2 = 4ax$, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.
Solution :
The given parabola is
$$y^2 = 4ax \quad …(i)$$
with vertex at the origin $O$.
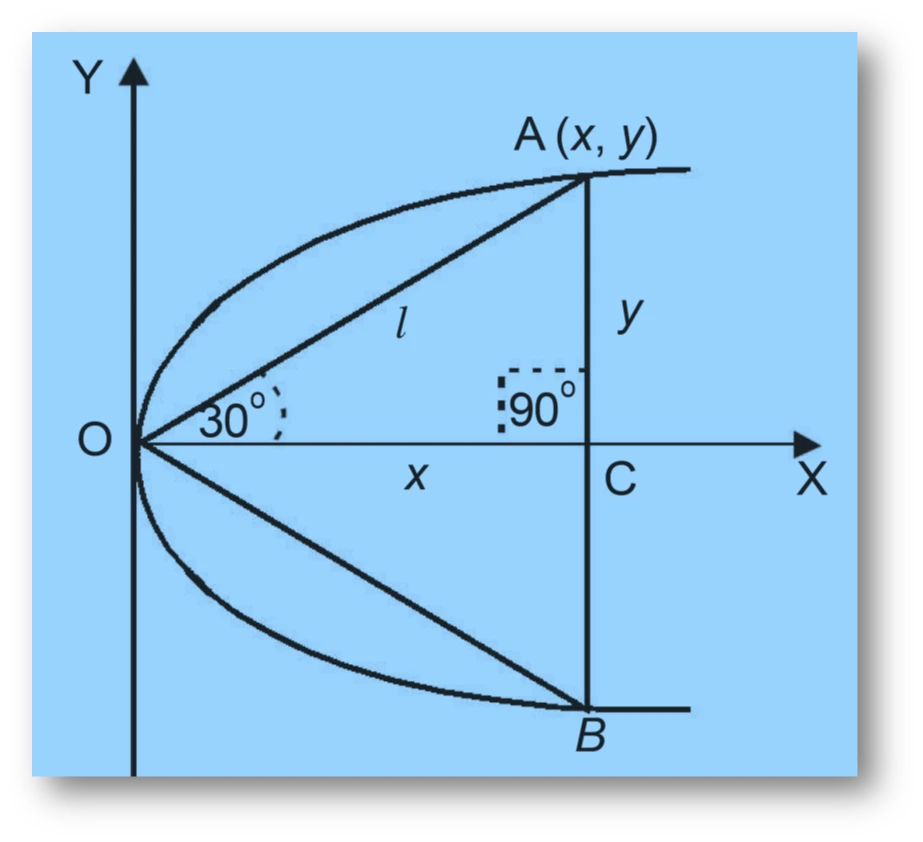
Let $OAB$ be the equilateral triangle inscribed in the parabola, with each side of length $l$. By symmetry, $AB \perp OX$ and $\angle AOB = 60^\circ$.
For point $A(x, y)$ on the parabola:
$$
\cos 30^\circ = \frac{x}{l} \Rightarrow x = \frac{\sqrt{3}}{2}l, \quad
\sin 30^\circ = \frac{y}{l} \Rightarrow y = \frac{l}{2}
$$
Coordinates of point $A$ are
$$\left( \frac{\sqrt{3}}{2}l, \frac{l}{2} \right)$$
Since $A$ lies on the parabola, its coordinates satisfy equation (i):
$$
y^2 = 4ax \Rightarrow \left(\frac{l}{2}\right)^2 = 4a \cdot \frac{\sqrt{3}}{2} l
$$
$$
\frac{l^2}{4} = 2\sqrt{3} a l \quad \Rightarrow \quad l^2 = 8 \sqrt{3} a l
$$
Dividing both sides by $l$,
$$
l = 8 \sqrt{3} a
$$
Hence, the length of side of equilateral triangle = $ 8 \sqrt{3} a $
$$
\boxed{l = 8 \sqrt{3} a}
$$


