NCERT Solutions for Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations are prepared by the expert teachers at ANAND CLASSES. These NCERT Solutions of Maths help students in solving problems quickly, accurately and efficiently.
Table of Contents
Exercise 5.1
Express each of the complex number given in the Exercises 1 to 10 in the form a + ib.
1. (5i)(-3i/5)
SOLUTION
5i × (-3i/5) = -3 × i2
Since, i2 = 1. Therefore,
-3 × i2 = -3 × (-1) = 3
(5i)(-3i/5) = 3 + i0
2. i9 + i19
SOLUTION
i9 + i19 = i(i2)4 + i(i2)9
Since, i2 = 1. Therefore,
i(i2)4 + i(i2)9 = i(-1)4 + i(-1)9
= i – i = 0
i9 + i19 = 0 + i0
3. i-39
SOLUTION
i-39 = 1/i39 = 1/i3.(i4)9
Since, i3 = -i and i4 = 1. Therefore,
= 1/i3.(i4)9 = 1/(-i)(1)
= 1/-i
Multiply and divide by i
1/-i × i/i
= i/i2
Since, i2 = -1. Therefore,
i/i2 = -i
i-39= 0 + i.1
4. 3(7 + i7) + i (7 + i7)
SOLUTION
3(7 + i7) + i (7 + i7) = 21 + i21 + i7 + i27
Since, i2 = -1. Therefore,
21 + i21 + i7 + i27
= 21 + i28 + (-1)7
= 21 – 7 + i28
= 14 + i28
3(7 + i7) + i (7 + i7) = 14 + i28
5. (1 – i) – ( -1 + i6)
SOLUTION
(1 – i) – ( -1 + i6) = 1 – i + 1 – i6
= 2 – i7
6. (1/5 + i2/5) – (4 + i5/2)
SOLUTION
(1/5 + i2/5) – (4 + i5/2) = 1/5 + i2/5 – 4 – i5/2
= 1/5 – 4 + i2/5 – i5/2
= -19/5 – i21/10
(1/5 + i2/5) – (4 + i5/2) = -19/5 – i21/10
7. [(1/3 + i7/3) + (4 + i1/3)] – (-4/3 + i)
SOLUTION
[(1/3 + i7/3) + (4 + i1/3)] – (-4/3 + i)
= [1/3 + i7/3 + 4 + i/3] + 4/3 – i
= 13/3 + i8/3 + 4/3 – i
= 17/3 + i5/3
[(1/3 + i7/3) + (4 + i1/3)] – (-4/3 + i) = 17/3 + i5/3
8. (1 – i)4
SOLUTION
(1 – i)4 = (1 – i)2(1 – i)2
= (1 + i2 – 2i)(1 + i2 – 2i)
Since, i2 = -1. Therefore,
(1 + i2 – 2i)(1 + i2 – 2i)
= (1 – 1 – 2i)2
= (-2i)2
= 4i2 = 4(-1) = -4
(1 – i)4 = -4 + i0
9. (1/3 + 3i)3
SOLUTION
(1/3 + 3i)3 = (1/3)3 + (3i)3 + 3(1/3)2(3i) + 3(3i)2(1/3)
= 1/27 + 27i3 + 9i(1/9) + 9i2
= 1/27 + 27i3 + i + 9i2
Since, i2 = -1 and i3 = -i. Therefore,
1/27 + 27i3 + 9i2 + i
= 1/27 – 27i – 9 + i
= 1/27 – 9 – 26i
= -242/27 – i26
(1/3 + 3i)3 = -242/27 – i26
10. (-2 – i1/3)3
SOLUTION
(-2 – i1/3)3 = (-2)3 + (-i/3)3 + 3(-2)(-i/3)2 + 3(-i/3)(-2)2
= -8 – i3/27 – 6(i2/9) – i(4)
= -8 – i3/27 – 2i2/3 – 4i
Since, i2 = -1 and i3 = -i. Therefore,
-8 – i3/27 – 2i2/3 – 4i
= -8 + i/27 + 2/3 – 4i
= 2/3 – 8 + i/27 – 4i
= -22/3 – 107i/27
(-2 – i1/3)3 = -22/3 – i107/27
Find the multiplicative inverse of each of the complex numbers given in the Exercises 11 to 13.
11. 4 – 3i
SOLUTION
Let 4 – 3i = z.
|z|2 = 42 + (-3)2 = 16 + 9 = 25
Multiplicative inverse of z is z-1.
z-1 = z̄/|z|2 = (4 + 3i)/25
= 4/25 + i3/25
12. √5 + 3i
SOLUTION
Let √5 – 3i = z.
|z|2 = (√5)2 + (3)2 = 5 + 9 = 14
Multiplicative inverse of z is z-1.
z-1 = z̄/|z|2 = (√5 – 3i)/14
= √5/14 – i3/14
13. -i
SOLUTION
Let -i = z.
|z|2 = (-1)2 = 1
Multiplicative inverse of z is z-1.
z-1 = z̄/|z|2 = (i)/1
= i
14. Express the following expression in the form of a + ib :
(3 + i√5) (3 – i√5)/((√3 + √2i) – (√3 – √2i))
SOLUTION
(3 + i√5) (3 – i√5)/{(√3 + √2i) – (√3 – √2i)}
= {32 – (i√5)2}/{√3 + √2i – √3 + √2i}
= (9 – 5i2)/(2√2i)
Since, i2 = -1. Therefore,
(9 – 5i2)/(2√2i)
= (9 + 5)/(2√2i) = 14/2√2i
= 7/√2i
Multiply and divide by √2i
7/√2i × √2i/√2i
= 7i√2/2i2
= -7i√2/2
(3 + i√5) (3 – i√5)/{(√3 + √2i) – (√3 – √2i)} = 0 – i7√2/2
Exercise 5.2
Find the modulus and the arguments of each of the complex numbers in Exercises 1 to 2.
1. z = -1 – i√3
SOLUTION
Let -1 = r cos θ and -√3 = r sin θ, where r is the modulus.
Square and add both:
(r cos θ)2 + (r sin θ)2 = (-1)2 + (-√3)2
r2 cos2 θ + r2 sin2 θ = 1 + 3
r2 (cos2 θ + sin2 θ) = 4
r2 = 4 … (cos2 A + sin2 A = 1)
r = 2 as r > 0
r cos θ = -1
2 cos θ = -1
cos θ = -1/2 = -cos π/3
r sin θ = -√3
2 sin θ = -√3
sin θ = -√3/2 = -sin π/3
sin θ and cos θ are both negative. This implies that θ lies in quadrant III.
arg (z) = θ = -(π – π/3) = -2π/3
Hence, modulus of the given complex number = 2 and argument of given complex number is -2π/3
2. z = -√3 + i
SOLUTION
Let -√3 = r cos θ and 1 = r sin θ, where r is the modulus.
Square and add both:
(r cos θ)2 + (r sin θ)2 = (-√3)2 + (1)2
r2 cos2 θ + r2 sin2 θ = 3 + 1
r2 (cos2 θ + sin2 θ) = 4
r2 = 4 … (cos2 A + sin2 A = 1)
r = 2 as r > 0
r cos θ = -√3
2 cos θ = -√3
cos θ = -√3/2 = -cos π/6
r sin θ = 1
2 sin θ = 1
sin θ = 1/2 = sin π/6
sin θ is positive while cos θ is negative. This implies that θ lies in quadrant II.
arg (z) = θ = π – π/6 = 5π/3
Hence, modulus of the given complex number = 2 and argument of given complex number is 5π/3
Convert each of the complex numbers given in Exercises 3 to 8 in the polar form:
3. 1 – i
SOLUTION
Let 1 = r cos θ and -1 = r sin θ, where r is the modulus.
Square and add both:
(r cos θ)2 + (r sin θ)2 = (1)2 + (-1)2
r2 cos2 θ + r2 sin2 θ = 1 + 1
r2 (cos2 θ + sin2 θ) = 2
r2 = 2 … (cos2 A + sin2 A = 1)
r = √2 as r > 0
r cos θ = 1
√2 cos θ = 1
cos θ = 1/√2 = cos π/4
r sin θ = -1
√2 sin θ = -1
sin θ = -1/√2 = -sin π/4
sin θ is negative while cos θ is positive. This implies that θ lies in quadrant IV.
θ = -π/4
Polar form of the given complex number will be
1 – i = r cos θ + i r sin θ
= √2 cos (-π/4) + i√2 sin (-π/4)
4. -1 + i
SOLUTION
Let -1 = r cos θ and 1 = r sin θ, where r is the modulus.
Square and add both:
(r cos θ)2 + (r sin θ)2 = (-1)2 + (1)2
r2 cos2 θ + r2 sin2 θ = 1 + 1
r2 (cos2 θ + sin2 θ) = 2
r2 = 2 … (cos2 A + sin2 A = 1)
r = √2 as r > 0
r cos θ = -1
√2 cos θ = -1
cos θ = -1/√2 = -cos π/4
r sin θ = 1
√2 sin θ = 1
sin θ = 1/√2 = sin π/4
sin θ is positive while cos θ is negative. This implies that θ lies in quadrant II.
θ = π – π/4 = 3π/4
Polar form of the given complex number will be
-1 + i = r cos θ + i r sin θ
= √2 cos (3π/4) + i√2 sin (3π/4)
5. -1 – i
SOLUTION
Let -1 = r cos θ and -1 = r sin θ, where r is the modulus.
Square and add both:
(r cos θ)2 + (r sin θ)2 = (-1)2 + (-1)2
r2 cos2 θ + r2 sin2 θ = 1 + 1
r2 (cos2 θ + sin2 θ) = 2
r2 = 2 … (cos2 A + sin2 A = 1)
r = √2 as r > 0
r cos θ = -1
√2 cos θ = -1
cos θ = -1/√2 = -cos π/4
r sin θ = -1
√2 sin θ = -1
sin θ = -1/√2 = -sin π/4
sin θ and cos θ are both negative. This implies that θ lies in quadrant III.
θ = -(π – π/4) = -3π/4
Polar form of the given complex number will be
-1 – i = r cos θ + i r sin θ
= √2 cos (-3π/4) + i√2 sin (-3π/4)
6. -3
SOLUTION
-3 = -3 + i0
Let -3 = r cos θ and 0 = r sin θ, where r is the modulus.
Square and add both:
(r cos θ)2 + (r sin θ)2 = (-3)2 + (0)2
r2 cos2 θ + r2 sin2 θ = 9 + 0
r2 (cos2 θ + sin2 θ) = 9
r2 = 9 … (cos2 A + sin2 A = 1)
r = 3 as r > 0
r cos θ = -3
3 cos θ = -3
cos θ = -1 = -cos 0
r sin θ = 0
3 sin θ = 0
sin θ = 0 = sin 0
sin θ is positive and cos θ is negative. This implies that θ lies in quadrant II.
θ = π – 0 = π
Polar form of the given complex number will be
-3 = r cos θ + i r sin θ
= 3 cos (π) + i3 sin (π)
7. √3 + i
SOLUTION
Let √3 = r cos θ and 1 = r sin θ, where r is the modulus.
Square and add both:
(r cos θ)2 + (r sin θ)2 = (√3)2 + (1)2
r2 cos2 θ + r2 sin2 θ = 3 + 1
r2 (cos2 θ + sin2 θ) = 4
r2 = 4 … (cos2 A + sin2 A = 1)
r = 2 as r > 0
r cos θ = √3
2 cos θ = √3
cos θ = √3/2 = cos π/6
r sin θ = 1
2 sin θ = 1
sin θ = 1/2 = sin π/6
sin θ and cos θ are both positive. This implies that θ lies in quadrant I.
θ = π/6
Polar form of the given complex number will be
√3 + i = r cos θ + i r sin θ
= 2 cos (π/6) + i2 sin (π/6)
8. i
SOLUTION
i = 0 + i
Let 0 = r cos θ and 1 = r sin θ, where r is the modulus.
Square and add both:
(r cos θ)2 + (r sin θ)2 = (0)2 + (1)2
r2 cos2 θ + r2 sin2 θ = 0 + 1
r2 (cos2 θ + sin2 θ) = 1
r2 = 1 … (cos2 A + sin2 A = 1)
r = 1 as r > 0
r cos θ = 0
1 cos θ = 0
cos θ = 0 = cos π/2
r sin θ = 1
1 sin θ = 1
sin θ = 1 = sin π/2
sin θ and cos θ are both positive. This implies that θ lies in quadrant I.
θ = π/2
Polar form of the given complex number will be
i = r cos θ + i r sin θ
= 1 cos (π/2) + i1 sin (π/2)
= cos (π/2) + i sin (π/2)
Exercise 5.3
Solve each of the following equations:
1. x2 + 3 = 0
SOLUTION
On comparing the given quadratic equation to ax2 + bx + c = 0, we get
a = 1, b = 0 and c = 3
Discriminant = b2 – 4ac = 02 – 4(1)(3) = 0 – 12 = -12
x = (-b ± √D)/2a = ±√-12/2 = ±√12i/2 as i = √-1
x = ±2√3i/2 = ±√3i
Hence, x = √3i or -√3i.
2. 2x2 + x + 1 = 0
SOLUTION
On comparing the given quadratic equation to ax2 + bx + c = 0, we get
a = 2, b = 1 and c = 1
Discriminant = b2 – 4ac = 12 – 4(2)(1) = 1 – 8 = -7
x = (-b ± √D)/2a
= (-1 ± √-7)/2(2) = (-1 ± √7i)/4 as i = √-1
x = (-1 ± √7i)/4
Hence, x = (-1 + √7i)/4 or (-1 – √7i)/4.
3. x2 + 3x + 9 = 0
SOLUTION
On comparing the given quadratic equation to ax2 + bx + c = 0, we get
a = 1, b = 3 and c = 9
Discriminant = b2 – 4ac = 32 – 4(1)(9) = 9 – 36 = -27
x = (-b ± √D)/2a
= (-3 ± √-27)/2(1) = (-3 ± √27i)/2 as i = √-1
= (-3 ± 3√3i)/2
x = 3(-1 ± √3i)/2
Hence, x = 3(-1 + √3i)/2 or (-1 – √3i)/2.
4. -x2 + x – 2 = 0
SOLUTION
On comparing the given quadratic equation to ax2 + bx + c = 0, we get
a = -1, b = 1 and c = -2
Discriminant = b2 – 4ac = 12 – 4(-1)(-2) = 1 – 8 = -7
x = (-b ± √D)/2a
= (-1 ± √-7)/2(-1) = -(-1 ± √7i)/2 as i = √-1
x = -(-1 ± √7i)/2
Hence, x = -(-1 + √7i)/2 or -(-1 – √7i)/2.
5. x2 + 3x + 5 = 0
SOLUTION
On comparing the given quadratic equation to ax2 + bx + c = 0, we get
a = 1, b = 3 and c = 5
Discriminant = b2 – 4ac = 32 – 4(1)(5) = 9 – 20 = -11
x = (-b ± √D)/2a
= (-3 ± √-11)/2(1) = (-3 ± √11i)/2 as i = √-1
x = (-3 ± √11i)/2
Hence, x = (-3 + √11i)/2 or (-3 – √11i)/2.
6. x2 – x + 2 = 0
SOLUTION
On comparing the given quadratic equation to ax2 + bx + c = 0, we get
a = 1, b = -1 and c = 2
Discriminant = b2 – 4ac = (-1)2 – 4(1)(2) = 1 – 8 = -7
x = (-b ± √D)/2a
= (1 ± √-7)/2(1) = (1 ± √7i)/2 as i = √-1
x = (1 ± √7i)/2
Hence, x = (1 + √7i)/2 or (1 – √7i)/2.
7. √2x2 + x + √2 = 0
SOLUTION
On comparing the given quadratic equation to ax2 + bx + c = 0, we get
a = √2, b = 1 and c = √2
Discriminant = b2 – 4ac = 12 – 4(√2)(√2) = 1 – 8 = -7
x = (-b ± √D)/2a
= (-1 ± √-7)/2(√2) = (-1 ± √7i)/2√2 as i = √-1
x = (-1 ± √7i)/2√2
Hence, x = (-1 + √7i)/2√2 or (-1 – √7i)/2√2.
8. √3x2 – √2 + 3√3 = 0
SOLUTION
On comparing the given quadratic equation to ax2 + bx + c = 0, we get
a = √3, b = -√2 and c = 3√3
Discriminant = b2 – 4ac = (-√2)2 – 4(√3)(3√3) = 2 – 36 = -34
x = (-b ± √D)/2a
= (-√2 ± √-34)/2(√3) = (-√2 ± √34i)/2√3 as i = √-1
x = (-√2 ± √34i)/2√3
Hence, x = (-√2 + √34i)/2√3 or (-√2 – √34i)/2√3.
9. x2 + x + 1/√2 = 0
SOLUTION
Multiply both sides of the given equation by √2:
√2x2 + √2x + 1 = 0
On comparing the obtained quadratic equation to ax2 + bx + c = 0, we get
a = √2, b = √2 and c = 1
Discriminant = b2 – 4ac = (√2)2 – 4(√2)(1) = 2 – 4√2 = 2(1 – 2√2)
x = (-b ± √D)/2a
= [-√2 ± √(2(1 – 2√2))]/2(√2)
= (-√2 ± √2√i(2√2-1)/2√2 as i = √-1
x = (-1 ± √(2√2 – 1)i)/2
Hence, x = (-1 + √(2√2 – 1)i)/2 or (-1 – √(2√2 – 1)i)/2.
10. x2 + x/√2 + 1 = 0
SOLUTION
Multiply both sides of the given equation by √2:
√2x2 + x + √2 = 0
On comparing the obtained quadratic equation to ax2 + bx + c = 0, we get
a = √2, b = 1 and c = √2
Discriminant = b2 – 4ac = (1)2 – 4(√2)(√2) = 1 – 8 = -7
x = (-b ± √D)/2a
= [-1 ± √-7]/2(√2)
= (-1 ± √7i)/2√2 as i = √-1
x = (-1 ± √7i)/2
Hence, x = (-1 + √7i)/2 or (-1 – √7i)/2.
Miscellaneous Exercise
1. Evaluate: [i18 + (1/i)25]3.
SOLUTION
[i18 + (1/i)25]3
= [i4(4) + 2 + 1/i4(6) + 1 ]3
= [(i4)4.i2 + 1/(i4)6.i1 ]3
Now, i4 = 1 and i2 = -1.
= [(1)4.(-1) + 1/(1)6.i]3
= [-1 + 1/i]3
Multiple and divide 1/i by i.
= [-1 + 1/i × i/i]3
= [-1 + i/i2]3
= (-1 + i/(-1))3
= (-1 – i)3
= (-1)3 + (-i)3 + 3(-1)2(-i) + 3(-i)2(-1)
= -1 – i3 – 3i – 3i2
= -1 – (-1)i – 3i – 3(-1)
= -1 + i – 3i + 3
= 2 – 2i
2. For any two complex numbers z1 and z2, prove that
Re (z1 z2) = Re z1 Re z2 – Imz1 Imz2.
SOLUTION
Let there be two complex numbers z1 = x1 + iy1 and z2 = x2 + iy2.
z1 z2 = (x1 + iy1)(x2 + iy2)
= x1x2 + ix2y1 + ix1y2 + i2y1y2
= x1x2 – y1y2 + i(x2y1 + x1y2) … as i2 = -1
Re (z1 z2) = x1x2 – y1y2
Re z1 Re z2 = (x1) (x2)
Imz1 Imz2 = (y1) (y2)
Re z1 Re z2 – Imz1 Imz2 = x1x2 – y1y2
Hence, proved that Re (z1 z2) = Re z1 Re z2 – Imz1 Imz2.
3. Reduce to standard form.
(1/(1 – 4i) – 2/(i + 1)) (3 – 4i)/(5 + i)
SOLUTION
{1/(1 – 4i) – 2/(i + 1)} (3 – 4i)/(5 + i)
= {(i + 1 – 2 + 8i)/(1 – 4i)(i + 1)} × (3 – 4i)/(5 + i)
= {(-1 + 9i)/(i – 4i2 – 4i + 1)} × (3 – 4i)/(5 + i)
= {(-1 + 9i)/(-4(-1) – 3i + 1)} × (3 – 4i)/(5 + i)
= {(-1 + 9i)/(5 – 3i)} × (3 – 4i)/(5 + i)
= {(-1 + 9i)(3 – 4i)}/(5 – 3i)(5 + i)
= (-3 + 4i + 27i – 36i2)/(25 + 5i – 15i – 3i2)
= (-3 + 31i – 36(-1))/(25 – 10i – 3(-1))
= (-3 + 31i + 36)/(25 – 10i + 3)
= (33 + 31i)/(28 – 10i)
= (33 + 31i)/2(14 – 5i)
Multiply and divide by 14 + 5i
(33 + 31i)/2(14 – 5i) × (14 + 5i)/(14 + 5i)
= (33 + 31i)(14 + 5i)/2(142– 52i2)
= (462 + 434i + 165i + 155i2)/2(196 – 25i2)
= (462 + 599i + 155(-1))/(392 – 50i2)
= (462 – 155 + 599i)/(392 – 50(-1))
= (307 + 599i)/(392 + 50)
= (307 + 599i)/(442)
= 307/442 + i599/442
Hence, the standard form will be 307/442 + i599/442.
4. If x – iy = √(a – ib)/√(c – id) prove that (x2 + y2)2 = (a2 + b2)/(c2 + d2).
SOLUTION
x – iy = √(a – ib)/√(c – id)
Multiply the numerator and denominator by c + id
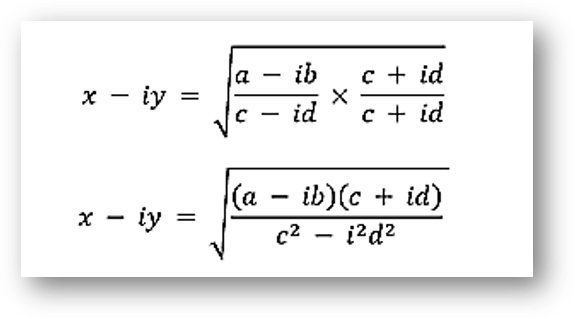
Square both sides

Comparing real and imaginary parts on both sides, we get:

5. Convert the following into the polar form:
(i) (1 + 7i)/(2 – i)2
SOLUTION
(1 + 7i)/(2 – i)2
= (1 + 7i)/(22 + i2 – 4i)
= (1 + 7i)/(4 – 1 – 4i)
= (1 + 7i)/(3 – 4i)
Multiply and divide by (3 + 4i)
(1 + 7i)/(3 – 4i) × (3 + 4i)/(3 + 4i)
= (1 + 7i)(3 + 4i)/(32 – 42i2)
= (3 + 21i + 4i + 28i2)/(9 – 16i2)
= (3 + 25i + 28(-1))/(9 – 16(-1))
= (3 + 25i – 28)/(9 + 16)
= (-25 + 25i)/25
= 25(-1 + i)/25
= -1 + i
Let -1 = r cos θ and 1 = r sin θ, where r is the modulus.
Square and add both:
(r cos θ)2 + (r sin θ)2 = (-1)2 + (1)2
r2 cos2 θ + r2 sin2 θ = 1 + 1
r2 (cos2 θ + sin2 θ) = 2
r2 = 2 … (cos2 A + sin2 A = 1)
r = √2 as r > 0
r cos θ = -1
√2 cos θ = -1
cos θ = -1/√2 = -cos π/4
r sin θ = 1
√2 sin θ = 1
sin θ = 1/√2 = sin π/4
sin θ is positive while cos θ is negative. This implies that θ lies in quadrant II.
θ = π – π/4 = 3π/4
Polar form of the given complex number will be
(1 + 7i)/(2 – i)2 = -1 + i = r cos θ + i r sin θ
= √2 cos (3π/4) + i√2 sin (3π/4)
(ii) (1 + 3i)/(1 – 2i)
SOLUTION
(1 + 3i)/(1 – 2i)
Multiply and divide by 1 + 2i
(1 + 3i)/(1 – 2i) × (1 + 2i)/(1 + 2i)
= (1 + 3i)(1 + 2i)/(12 – 22i2)
= (1 + 3i + 2i + 6i2)/(1 – 4i2)
= (1 + 5i + 6(-1))/(1 – 4(-1))
= (1 + 5i – 6)/(1 + 4)
= (-5 + 5i)/5
= 5(-1 + i)/5
= -1 + i
Let -1 = r cos θ and 1 = r sin θ, where r is the modulus.
Square and add both:
(r cos θ)2 + (r sin θ)2 = (-1)2 + (1)2
r2 cos2 θ + r2 sin2 θ = 1 + 1
r2 (cos2 θ + sin2 θ) = 2
r2 = 2 … (cos2 A + sin2 A = 1)
r = √2 as r > 0
r cos θ = -1
√2 cos θ = -1
cos θ = -1/√2 = -cos π/4
r sin θ = 1
√2 sin θ = 1
sin θ = 1/√2 = sin π/4
sin θ is positive while cos θ is negative. This implies that θ lies in quadrant II.
θ = π – π/4 = 3π/4
Polar form of the given complex number will be
(1 + 7i)/(2 – i)2 = -1 + i = r cos θ + i r sin θ
= √2 cos (3π/4) + i√2 sin (3π/4)
Solve each of the equation in Exercises 6 to 9.
6. 3x2 – 4x + 20/3 = 0
SOLUTION
Multiply both sides of the given equation by 3:
9x2 – 12x + 20 = 0
On comparing the obtained quadratic equation to ax2 + bx + c = 0, we get
a = 9, b = -12 and c = 20
Discriminant = b2 – 4ac = (-12)2 – 4(9)(20) = 144 – 720 = -576
x = (-b ± √D)/2a
= [-(-12) ± √-576]/2(9)
= (12 ± √576i)/18 as i = √-1
= (12 ± 24i)/18
= 6(2 ± 4i)/18
= (2 ± 4i)/3
x = (2 ± 4i)/3
Hence, x = (2 + 4i)/3 or (2 – 4i)/3.
7. x2 – 2x + 3/2 = 0
SOLUTION
Multiply both sides of the given equation by 2:
2x2 – 4x + 3 = 0
On comparing the obtained quadratic equation to ax2 + bx + c = 0, we get
a = 2, b = -4 and c = 3
Discriminant = b2 – 4ac = (-4)2 – 4(2)(3) = 16 – 24 = -8
x = (-b ± √D)/2a
= [-(-4) ± √-8]/2(2)
= (4 ± √8i)/4 as i = √-1
= (4 ± 2√2i)/4
= 2(2 ± √2i)/4
= (2 ± √2i)/2
x = (2 ± √2i)/2
Hence, x = (2 + √2i)/2 or (2 – √2i)/2.
8. 27x2 – 10x + 1 = 0
SOLUTION
On comparing the obtained quadratic equation to ax2 + bx + c = 0, we get
a = 27, b = -10 and c = 1
Discriminant = b2 – 4ac = (-10)2 – 4(27)(1) = 100 – 108 = -8
x = (-b ± √D)/2a
= [-(-10) ± √-8]/2(27)
= (10 ± √8i)/54 as i = √-1
= (10 ± 2√2i)/54
= 2(5 ± √2i)/54
= (5 ± √2i)/27
x = (5 ± √2i)/27
Hence, x = (5 + √2i)/27 or (5 – √2i)/27.
9. 21x2 – 28x + 10 = 0
SOLUTION
On comparing the obtained quadratic equation to ax2 + bx + c = 0, we get
a = 21, b = -28 and c = 10
Discriminant = b2 – 4ac = (-28)2 – 4(21)(10) = 784 – 840 = -56
x = (-b ± √D)/2a
= [-(-28) ± √-56]/2(21)
= (28 ± √56i)/42 as i = √-1
= (28 ± 2√14i)/42
= 2(14 ± √14i)/42
= (14 ± √14i)/21
x = (14 ± √14i)/21
Hence, x = (14 + √14i)/21 or (14 – √14i)/21.
10. If z1 = 2 – i, z2 = 1 + i, find |(z1 + z2 + 1)/(z1 – z2 + 1)|.
SOLUTION
|(z1 + z2 + 1)/(z1 – z2 + 1)|
= |(2 – i + 1 + i + 1)/(2 – i – 1 – i + 1)|
= |(2 + 2)/(2 – 2i)|
= |2(2)/2(1 – i)|
= |2/(1 – i)|
Multiply and divide by 1 + i
|2/(1 – i) × (1 + i)/(1 + i)|
= |2(1 + i)/(12 – i2)|
= |2(1 + i)/(12 – (-1))|
= |2(1 + i)/2|
= |1 + i| =|1 + 1i|
= √(12 + 12)
= √(1 + 1) = √2
Hence, |(z1 + z2 + 1)/(z1 – z2 + 1)| = √2.
11. If a + ib = (x + i)2/(2x2 + 1), prove that a2 + b2 = (x2 + 1)2/(2x2 + 1)2.
SOLUTION
a + ib = (x + i)2/(2x2 + 1)
= (x2 + i + 2ix)/(2x2 + 1)
= (x2 + (-1) + 2ix)/(2x2 + 1)
= (x2– 1)/(2x2 + 1) + 2ix/(2x2 + 1)
Compare the real and imaginary parts on both sides
a = (x2 – 1)/(2x2 + 1) AND b = 2x/(2x2 + 1)
Square both sides
a2 = [(x2 – 1)/(2x2 + 1)]2 AND b2 = [2x/(2x2 + 1)]2
Add both equations
a2 + b2 = [(x2 – 1)/(2x2 + 1)]2 + [2x/(2x2 + 1)]2
= {x4 + 1 – 2x2 + 4x2}/(2x2 + 1)2
= {x4 + 1 + 2x2}/(2x2 + 1)2
= {(x2)2 + 12 + 2(1)(x2)}/(2x2 + 1)2
= (x2 + 1)2/(2x2 + 1)2
Hence, proved.
12. Let z1 = 2 – i, z2 = -2 + i. Find
(i) Re (z1z2/z̄1), (ii) Im (1/z1z̄2).
SOLUTION
(i) z1z2 = (2 – i)(-2 + i)
= -4 + 2i + 2i – i2
= -4 + 4i – (-1)
= -4 + 1 + 4i
= -3 + 4i
z̄1 = 2 + i
z1z2/z̄1 = (-3 + 4i)/(2 + i)
Multiply the numerator and denominator by 2 – i
z1z2/z̄1 = (-3 + 4i)/(2 + i) × (2 – i)/(2 – i)
= (-3 + 4i)(2 – i)/(22 – i2)
= (-6 + 8i + 3i – 4i2)/(4 – (-1))
= (-6 + 11i – 4(-1))/(4 + 1)
= (-6 + 11i + 4)/5
= (-2 + 11i)/5
= -2/5 + i11/5
Re (z1z2/z̄1) = -2/5
(ii) z1z̄1 = (2 – i)(2 + i) = 4 – i2 = 4 – (-1)
= 4 + 1 = 5
1/z1z̄1 = 1/5 + 0i
Im (1/z1z̄1) = 0
13. Find the modulus and argument of the complex number (1 + 2i)/(1 – 3i).
SOLUTION
Let z = (1 + 2i)/(1 – 3i).
Multiple and divide by 1 + 3i
z = (1 + 2i)/(1 – 3i) × (1 + 3i)/(1 + 3i)
= (1 + 2i)(1 + 3i)/(12 – 92i2)
= (1 + 2i + 3i + 6i2)/(1 – 9(-1))
= (1 + 5i + 6(-1))/(1 + 9)
= (-5 + 5i)/10
= 5(-1 + i)/10
= (-1 + i)/2
Let -1/2 = r cos θ and 1/2 = r sin θ, where r is the modulus.
Square and add both:
(r cos θ)2 + (r sin θ)2 = (-1/2)2 + (1/2)2
r2 cos2 θ + r2 sin2 θ = 1/4 + 1/4
r2 (cos2 θ + sin2 θ) = 1/2
r2 = 1/2 … (cos2 A + sin2 A = 1)
r = 1/√2 as r > 0
r cos θ = -1/2
1/√2 cos θ = -1/2
cos θ = -1/√2 = -cos π/4
r sin θ = 1/2
1/√2 sin θ = 1/2
sin θ = 1/√2 = sin π/4
sin θ is positive while cos θ is negative. This implies that θ lies in quadrant II.
arg (z) = θ = (π – π/4) = 3π/4
Hence, modulus of the given complex number = 1/√2 and argument of given complex number is 3π/4
14. Find the real numbers x and y if (x – iy) (3 + 5i) is the conjugate of -6 – 24i.
SOLUTION
(x – iy)(3 + 5i) = 3x – 3iy + 5ix – 5i2y
= 3x – 3iy + 5ix – 5(-1)y
= 3x + 5y + i(5x – 3y)
Let z = -6 – 24i
Then, 3x + 5y + i(5x – 3y) = z̄
Therefore,
3x + 5y – i(5x – 3y) = z
3x + 5y – i(5x – 3y) = -6 – 24i
Compare the real and imaginary parts on both the sides
3x + 5y = -6
3x = -6 -5y
x = (-6 – 5y)/3
AND
-(5x – 3y) = -24
5x – 3y = 24
5(-6 – 5y)/3 – 3y = 24
(-30 – 25y – 9y)/3 = 24
-30 – 34y = 72
-34y = 102
y = -3
x = (-6 – 5(-3))/3
= (-6 + 15)/3
= 9/3
x = 3
Hence, x = 3 and y = -3.
15. Find the modulus of (1 + i)/(1 – i) – (1 – i)/(1 + i).
SOLUTION
Let z = (1 + i)/(1 – i) – (1 – i)/(1 + i)
z = {(1 + i)2 – (1 – i)2}/(1 – i)(1 + i)
= {1 + i2 + 2i – 1 – i2 + 2i}/(1 – i2)
= (4i)/(1 – (-1))
= 4i/(1 + 1)
= 4i/2 = 2i
Modulus of the given complex number = |z| = |2i| = √(22) = 2
16. If (x + iy)3 = u + iv, then show that
u/x + v/y = 4(x2 – y2)
SOLUTION
(x + iy)3 = u + iv
x3 + i3y3 + 3(x2)(iy) + 3(i2y2)(x) = u + iv
x3 + (-i)y3 + 3x2yi + 3(-1)xy2 = u + iv
x3 – iy3 + 3x2yi – 3xy2 = u + iv
x3 – 3xy2 + 3x2yi – iy3 = u + iv
(x3 – 3xy2) + i(3x2y – y3) = u + iv
Comparing real and imaginary parts on both sides, we get
x3 – 3xy2 = u AND 3x2y – y3 = v
Now,
u/x + v/y = (x3 – 3xy2)/x + (3x2y – y3)/y
= x(x2 – 3y2)/x + y(3x2 – y2)/y
= x2 – 3y2 + 3x2 – y2
= 4x2 – 4y2
= 4(x2 – y2)
Hence, proved.
17. If α and β are different complex numbers with |β| = 1, then find
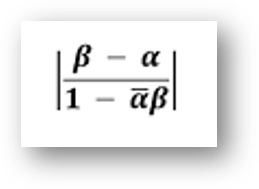
SOLUTION
Let α = a + ib and β = x + iy
|β| = 1
|x + iy| = 1
√(x2+ y2) = 1
x2 + y2 = 1

Hence, proved.
18. Find the number of non-zero integral solutions of the equation |1 – i|x = 2x.
SOLUTION
|1 – i|x = 2x
[√(12 + (-1)2)]x = 2x
(√2)x = 2x
2x/2 = 2x
Compare the exponents
x/2 = x
x = 2x
2x – x = 0
x = 0
0 is the only possible solution for the given equation.
Hence, there are no non-zero integral solutions of the given equation.
19. If (a+ib) (c+id) (e+if) (g+ih) = A +iB, then show that
(a2+b2) (c2+d2) (e2+f2) (g2+h2) = A2+ B2
SOLUTION
(a+ib) (c+id) (e+if) (g+ih) = A +iB
Take modulus on both the sides
|(a+ib) (c+id) (e+if) (g+ih)| = |A +iB|
√(a2 + b2) √(c2 + d2) √(e2 + f2) √(g2 + h2) = √(A2 + B2)
Square both sides
(a2 + b2)(c2 + d2)(e2 + f2)(g2 + h2) = (A2 + B2)
Hence, proved.
20. If (1 + i)m/(1 – i)m = 1, then find the least positive integral value of m.
SOLUTION
[(1 + i)/(1 – i)]m = 1
Multiply and divide by (1 + i)m
[(1 + i)/(1 – i) × (1 + i)/(1 + i)]m = 1
[(1 + i)2/(12 – i2)]m = 1
[(1 + i2 + 2i)/(1 – (-1))]m = 1
[(1 – 1 + 2i)/(1 + 1))]m = 1
(2i/2)m = 1
im = 1
We know that i4k = 1 for some integer k.
im = i4k
m = 4k
Hence, least positive integral value of m is 4 × 1 = 4.
- NCERT Solutions for Complex Numbers & Quadratic Equations
- Complex Numbers & Quadratic Equations NCERT PDF
- Free PDF download NCERT Solutions Class 11 Maths
- NCERT Class 11 Complex Numbers & Quadratic Equations solutions
- CBSE Class 11 Maths Chapter 5 solutions
- NCERT solved examples Complex Numbers & Quadratic Equations
- Important questions Complex Numbers & Quadratic Equations
- NCERT step-by-step solutions for Quadratic Equations
- JEE Complex Numbers & Quadratic Equations NCERT PDF
- NCERT Maths Chapter 5 Class 11 solutions PDF
- Free NCERT Maths Class 11 Complex Numbers PDF
- NCERT Quadratic Equations and Complex Numbers MCQs
- CBSE board exam questions Complex Numbers & Quadratic Equations
- NCERT exemplar Complex Numbers & Quadratic Equations solutions
- NCERT textbook solutions Complex Numbers PDF


