The process of finding the anti-derivative of a function is the inverse process of differentiation i.e. finding integral is the inverse process of differentiation. Integration can be used to find the area or volume of a function with or without certain limits or boundaries
It is shown as
∫g(x)dx = G(x) + C
Explanation:
It means integral of function “g(x)” with respective “x”
G(x) represents the anti-derivative and can also state that the derivative of G(x) w.r.t x is g(x)
g(x) is the integrand on which integration is performed
dx is integrating agent
C is called integration constant
With a diagram
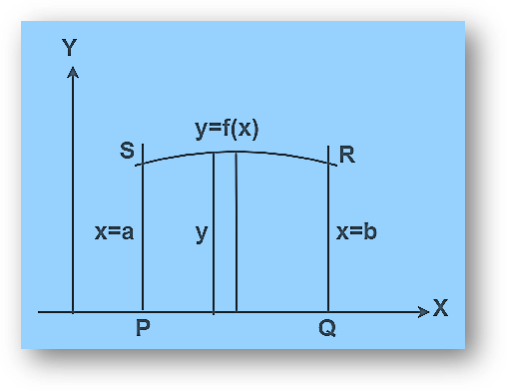
Lets us say we need to find an Area Under a Curve let the function be f(x)
The area can be found by integrating the function between the boundaries a and b
let us say ∫ f(x)dx = F(x)
the area under the curve given as F(b)-F(a) given ‘b’ as the upper limit and ‘a’ as the lower limit
Integration for some standard function
∫ a dx = ax+ C ;Where a is constant
∫ xn dx = ((xn+1)/(n+1))+C ; n≠1.
∫ sin x dx = – cos x + C.
∫ cos x dx = sin x + C.
∫ sec2 x dx = tan x + C.
Table of Contents
Integration by Substitution
Integration of a few standard functions is given, but to find out the integrals of various functions apart from basic functions we apply different methods to bring the functions to basic functions format so that integration can be performed. One of those methods is the Integration by substitution method.
The chain rule used to perform differentiation is applied in a reverse format which is why this method is also called as reverse chain rule or u-substitution method.
In this method, the integral function is transformed into another format i.e. into the simplest form by replacing or substituting independent variables like “x” with others
Example: ∫(3x2-5)(6x)dx
Solution:
Let us assume 3x2-5=t
performing the differentiation on both sides
6x.dx=dt
Now substitute 3x2-5 as “t” and 6x.dx as dt in the given we get
∫t.dt
w.k.t( i.e. We Know That)
∫ xn dx = ((xn+1)/(n+1))+C ; n ≠ 1
applying this standard formula we get (t2)/2+c
replacing t with 3x2-5
The answer is ((3x2-5)2)/2
When to apply the Integration by Substitution method
To find integral by using this method it needs to be present in a specific format and the general form is given as
∫ f(g(x)).g'(x).dx = f(t).dt
where g(x)=t
g'(x).dx=dt
∫f(t).dt=F(t)+c=F(g(x))+c
We substitute g(x) with t and convert it into a simple or standard function format and perform the integration and finally replace t with g(x)
Sample Problems
Question 1: ∫tan x dx
Solution:
∫(sin x/cos x).dx
let us assume cos x=t
performing the differentiation on both sides
-sin x.dx=dt
=-∫dt/t
w.k.t∫1/t=ln |t| ….(w.k.t. = We Know That )
=-ln |t|
replacing t with cos x
=-ln |cos x| or ln |sec x|
Question 2: ∫cot x dx
Solution:
∫(cos x/sin x)dx
assume sin x=t
performing the differentiation on both sides
cos x.dx=dt
=∫dt/t
w.k.t∫1/t=ln|t|
=ln|t|
replacing t with sin x
=ln |sin x| or -ln |cos x|
Question 3: ∫sec x dx
Solution:
It can be rewritten as ∫(sec x (sec x+tan x))/(sec x+tan x) dx
let us assume secx+tanx=t
performing the differentiation on both sides
(sec x.tan x+sec2 x)dx=dt
sec x(tan x+sec x).dx=dt
=∫dt/t
w.k.t∫1/t=ln|t|
=ln|t|
replacing t with secx+tanx
=ln |secx+tanx|
Question 4: ∫cosec x dx
Solution:
It can be rewritten as
=∫(cosec x(cosec x+cot x))/(cosec x+cot x) dx
let us assume cosec x+cot x=t
(-cosec x.cot x-cosec2 x)dx=dt
-cosec x(cot x+cosec x)dx=dt
=-∫dt/t
w.k.t∫1/t=ln |t|
=ln |t|
replacing t with cosec x +co tx
=ln |cosec x + cot x|
Question 5: ∫x.sin(8+2x2)dx
Solution:
Assume 8+2x2=t
performing the differentiation on both sides
4xdx=dt
xdx=dt/4
=1/4∫sin(t)dt
wkt ∫ sin x dx = – cos x + C.
=1/4∫sin(t)dt=1/4(-cost)+c
replacing t with 8+2(x^2)
=(-cos(8+2x2))/4+C
Question 6: ∫(2w-4)(2w2-8w+10)3.dw
Solution:
Assume 2w2-8w+10=t
performing the differentiation on both sides
(4w-8)dw=dt
(2w-4)dw=dt/2
=1/2(∫t3.dt)
∫ xn dx = ((xn+1)/(n+1))+C ; n≠1
=1/2(∫t3.dt)=(1/2).(1/4)(t4)+C
replacing t with 2w2-8w+10
=1/8((2w2-8w+10)4)+C
Question 7: ∫p/(1+5p2).dp
Solution:
Assume 1+5p2=t
performing the differentiation on both sides
10pdp=dt
pdp=dt/10
=1/10(∫dt/t)
w.r.t ∫1/p=|logp|+C
=1/10(|logt|)+C
replacing t with 1+5p2
=1/10(|log(1+5p2)|)+C
Question 8: ∫cos(8x + 8) dx
Solution:
Assume 8x+8=t
performing the differentiation on both sides
8dx=dt
1/8(∫cost dt)
w.r.t ∫ cos x dx = sin x + C.
1/8(∫cost dt)=1/8(sint)+C
replacing t with 8x+8
1/8(sin(8x+8))+C
Question 9: ∫(3sin x).cos x.dx
Solution:
Assume sin x=t
performing the differentiation on both sides
cos x.dx=dt
=∫(3t)dt
w.r.t ∫ ax dx = (ax/ln a) + C ; a>0, a≠1
=∫(3t)dt=(3t)/ln 3
replacing t with sinx
=(3^sinx)/ln 3
Practice Problems – Integration by Substitution Formula
Try out the given problems to master the concept of Integration by Substitution :
Q1 : ∫ [(ln (x))ⁿ/x] dx
Q2 : ∫ [(Sin⁻¹(x))³/√(1-x²)] dx
Q3 : ∫ [2x(e)^(x²)] dx
Q4 : ∫ [x/√(1+x²)] dx
Q5 : ∫ Cos(3x)Sin(3x) dx
Q6 : ∫ [2x/(1+x²)] dx
Q7 : ∫ [x√(1-x²)] dx
Q8 : ∫ 2 e^(2x) dx
Q9 : ∫ (2x + 1)/(x² + x + 1) dx
Q10 : ∫ [Sin( ln(x)) . (1/x)] dx
Hint for Q3 -> Let u = 3x and Use identity : Sin(2u) = 2 Sin(u) Cos(u) , then let v = 2u.
FAQs on Integration by Substitution
What is integration by substitution?
Integration by substitution is a method used to evaluate integrals. It involves changing the variable of integration to simplify the integral. This technique is analogous to the chain rule for differentiation.
What is the formula for integration by substitution?
The formula for integration by substitution is:
∫f(g(x))g'(x) dx = ∫f(u) du
where , u = g(x)
How do you choose the substitution u?
Choosing the substitution u typically involves identifying a function inside the integral whose derivative is also present in the integral. Often, u is set to be the inner function in a composite function.
What if the integral doesn’t match exactly after substitution?
If the integral doesn’t match exactly after substitution, you may need to manipulate the integral algebraically. For instance, you might factor out constants or split the integral into parts.
Can integration by substitution be used for definite integrals?
Yes, integration by substitution can be used for definite integrals. However, you need to change the limits of integration according to the substitution as :
What are Common Mistakes to Avoid?
- Forgetting to change the limits of integration when dealing with definite integrals.
- Not simplifying the integral properly after substitution.
- Incorrectly differentiating or integrating functions.
Are there any functions that are particularly suited for substitution?
Functions involving compositions such as polynomials within trigonometric, exponential, or logarithmic functions often goes well with substitution method. Identifying an inner function whose derivative is present in the integral is key here.

