Operations on Sets-Union of Sets, Intersection of Sets, Difference of Sets, Complement of Sets | Class 11 Math Notes Study Material Download Free PDF

Sets are fundamental in mathematics and are collections of distinct objects, considered as a whole. In this topic, we will explore the basic operations you can perform on sets, such as union, intersection, difference, and complement. These operations help us understand how sets interact with each other and allow us to solve various problems in mathematics and beyond.

What is Set?

A set is a well-defined collection of objects.

The objects may be numbers, alphabets, names of people, etc. Sets are represented using upper-case letters such as A, B, etc. For Example,

A = {a, e, i, o, u} OR A is a set of vowels in the English alphabet.

Note: “B = collection of good students” is not a set because we don’t know the criteria for good students. Thus there is some ambiguity as to which students belong to the set and which do not.

Operations on Sets

• Union of Sets
• Intersection of Sets  
• Difference of Sets
• Complement of Sets

Intersection of Sets  

The intersection of two sets A and B is a set that contains all the elements that are common to both A and B. Formally it is written as 

A ∩ B = {x : x ∈ A and x ∈ B}

In the following image, the shaded area is the intersection of sets A and B

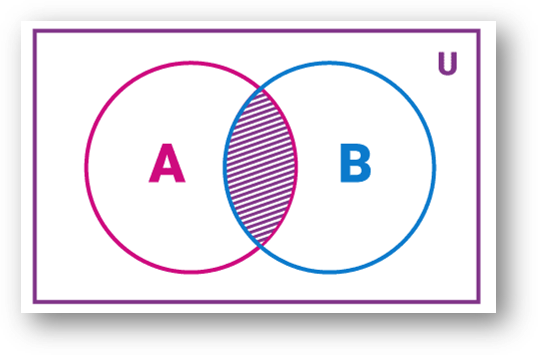
Example: 

If A = {2, 3, 5, 7} and B = {1, 2, 3, 4, 5}
then the intersection of set A and B is the set A ∩ B = {2, 3, 5} 

In this example 2, 3, and 5 are the only elements that belong to both sets A and B. 

Union of Sets

Union of two sets A and B is a set that contains all the elements that are in A or in B or in both A and B. Formally it is written as

A ∪ B = {x : x ∈ A or x ∈ B}

In the following image, the shaded area is the union of sets A and B.

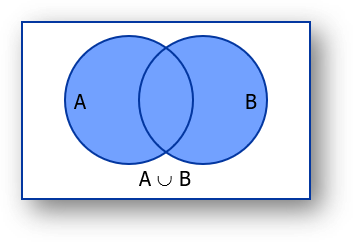
Example: 

If A = {2, 4, 8} and B = {2, 6, 8}
then the union of A and B is the set A ∪ B = {2, 4, 6, 8}

In this example, 2, 4, 6, and 8 are the elements that are found in set A or in set B or in both sets A and B

Complement or Difference Between Sets

The relative complement or set difference of two sets A and B is the set containing all the elements that are in A but not in B. Formally this is written as 

A − B = {x: x ∈ A and x ∉ B}

In the following image, the shaded area represents the difference set of set A and set B

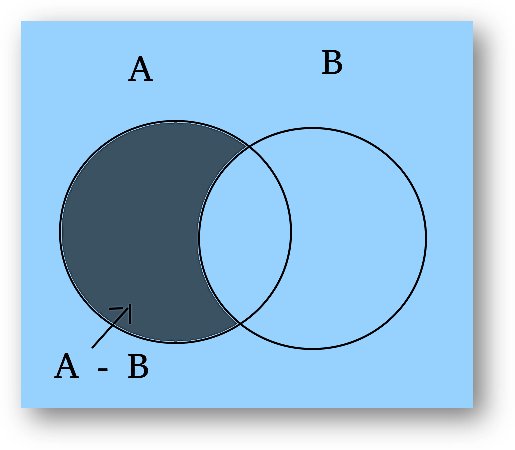
Note:  A – B is equivalent to A ∩ B’ i.e.,  A – B = A ∩ B’

Example: 

If A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and B = {2, 3, 5, 7}
then A – B = {1, 4, 6, 8, 9, 10}
and further B – A = ∅

Universal Set and Absolute Complement

Universal set

A universal set is the set of all objects currently under consideration. It is usually denoted by the upper-case letter U. For example for a set of vowels, the universal set may be the set of alphabets.

Note: A set is always a subset of the universal set. 

A ⊆ U

Absolute complement

The absolute complement of a set A is the set of all elements that are in U but not in A. It is denoted as A’. In the following image, the shaded area represents the complement of set A

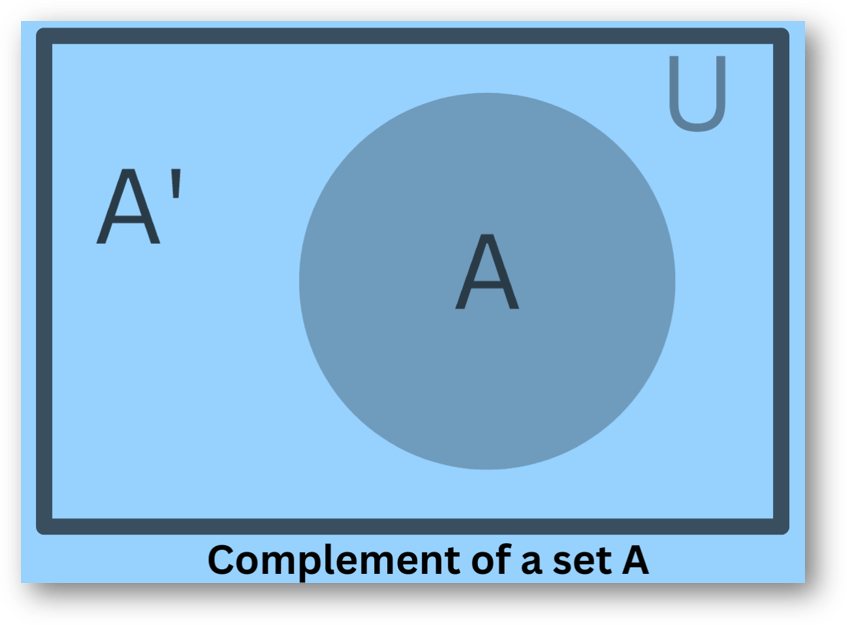
The absolute complement is sometimes just called complement.

Note: A’ is equivalent to U – A i.e.,  A’ = U – A

Example: 

If U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and A = {1, 2, 3}
then A’ = {4, 5, 6, 7, 8, 9, 10} = U – A

Subset and Proper Subset

Subset

For two set A and B, A is a subset of B if every element in A is also in B. A can be equal to B. This is formally written as  

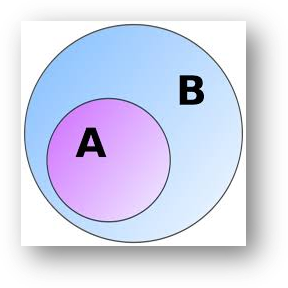
In the following image, set A is a subset of B

A ⊆ B

Example: 

If A = {2, 4} and B = {1, 2, 3, 4, 5, 6, 7, 8}
then A is a subset of B

In this example, A is a subset of B, because all the elements in A are also in B

Notes: 

1. An empty set (or null set) is a subset of every set.

Example: 

∅ is a subset of the set {1, 2, 3, 4}

2. For a set A, the number of possible subsets is 2^|A|. Where |A| = number of elements in A.

Example: 

For the set C = {1, 2, 3}, there are 2³ = 8 possible subsets
they are ∅, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, {1, 2, 3}

Proper subset (also called strict subset)

For two sets A and B, A is a proper subset of B, if A is a subset of B and A is not equal to B. Formally it is written as 

B⊇A  if  A⊆B

Example: 

For a set B = {1, 2, 3},
∅, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3} are all proper subsets of B
Note that {1, 2, 3} is not a proper subset of B, because they are equal

Superset and Proper Superset

Superset

For two sets A and B, if A is a subset of B then B is the superset of A. A can be equal to B. Formally it is denoted as 

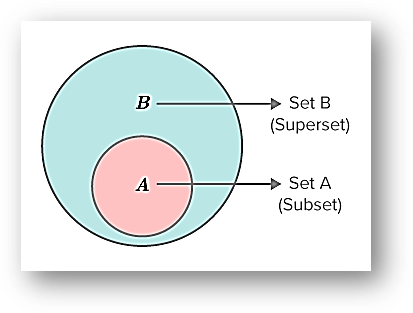
In the following image, set B is the superset of set A

B⊃A, if A⊆B and A ≠ B

Examples: 

• If A = {2, 4} and B = {1, 2, 3, 4, 5, 6, 7, 8}
  then B is the superset of A, because A is a subset of B
   
• If A = {11, 12} and B = {11, 12 } then B is the super set of A

Proper superset (also called strict superset)

For two sets A and B, if A is a subset of B and A is not equal to B, then B is the proper superset of A. Formally it is written as 

Examples: 

• If A = {1, 2, 3} and B = {0, 1, 2, 3, 4, 5}
  then B is a proper superset of A, because A is a subset of B and A ≠ B  
   
• If A = {2, 4, 6} and B = {2, 4, 6} then B is not a proper superset of A, because A = B 

Bringing the Set Operations Together

De Morgan’s laws

1. The complement of the union of two sets is equal to the intersection of their complements
   i.e.,  (A ∪ B)’ = A’ ∩ B’
2. The complement of the intersection of two sets is equal to the union of  their complements
   i.e.,  (A ∩ B)’ = A’ ∪ B’

Formula for the Cardinality of Union and Intersection

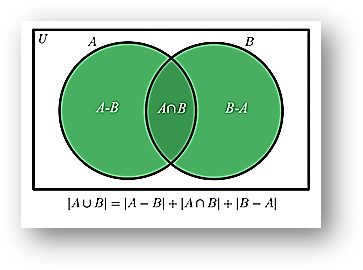
The formula for the Cardinality of Union and Intersection is given below:

∣A ∪ B∣ = ∣A∣ + ∣B∣ − ∣A ∩ B∣ 

Proof:

We can write
    |A ∪ B| = |A – B| + |A ∩ B| + |B – A|               —- by the sum of disjoint sets, refer to the Venn diagram above
    |A ∪ B| = (|A| – |A ∩ B|) + |A ∩ B| + |B – A|    —- Substitute |A – B| = |A| – |A ∩ B|
    |A ∪ B| = |A| + |B – A|                           —- Simplify
    |A ∪ B| = |A| + |B| – |A ∩ B|                  —- Substitute |B – A| = |B| – |A ∩ B|)

Problems on Operations on Sets – Union & Intersection

Problem 1: There are 100 students in a class, 45 students said that they liked apples, and 30 of the students said that they liked both apples and oranges. Every student has to choose at least one of the two fruits. Find how many students like oranges.

Solution:

Let U = set of all students in the class
      A = set of students that like apples
      B = set of students that like oranges

Given: 
    |A| = 45
    |A ∩ B| = 30
    |U| = |A ∪ B| = 100 (because every student has to choose)

We need to find how many like oranges. i.e., |B|

The formula to be used is,
    |A ∪ B| = |A| + |B| – |A ∩ B|        —-(i)

Subtract |A| – |A ∩ B| from both sides in (i) to get
    |A ∪ B| – (|A| – |A ∩ B|) = |B|
or |B| = |A ∪ B| – (|A| – |A ∩ B|)

Substitute the given values and simplify,
    |B| = |A ∪ B| – (|A| – |A ∩ B|)
         = 100 – ( 45 -30 )
         = 85

Thus the number of students that like oranges is 85.

Problem 2: There are a total of 120 students in a class. 70 of them study mathematics, 40 study science, and 10 students study both mathematics and science. Find the number of students who
    i) Study mathematics but not science
    ii) Study science but not mathematics
    iii) Study mathematics or science

Solution:  

Let,
   U = set of all students in the class
   M = set of students that study mathematics
   S = set of students that study science

Our universal set here has 120 student i.e, |U| = 120

Given,
    |M| = 70
    |S| = 40
    |M ∩ S| = 10  (number of students that study both mathematics and science)

i) Finding the number of students that study mathematics but not science. In the following image, the shaded area represents the set of students that study mathematics but not science.

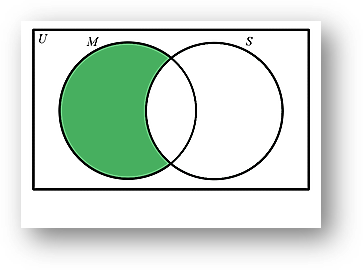
We are required to find |M – S|
By the Venn diagram, we can see that |M – S| can be written as |M| – |M ∩ S|
thus,
    |M – S| = |M| – |M ∩ S|
               = 70 – 10
               = 60

Thus the number of students who study mathematics but not science is 60

ii)  Finding the number of students that study science but not mathematics.  In the following image, the shaded area represents the set of students that study science but not mathematics

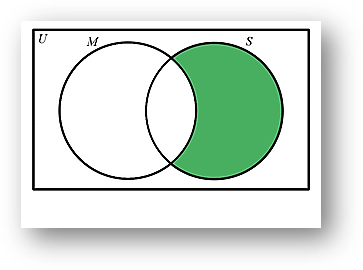
We are required to find |S – M|
By the Venn diagram, we can see that |S – M| can be written as |S| – |M ∩ S|
thus,    
    |S – M| = |S| – |M ∩ S|
               = 40 – 10
               = 30

Thus the number of students who study science but not mathematics is 30

iii) Finding the number of students who study mathematics or science.  In the following image, the shaded area represents the set of students that study mathematics or science.

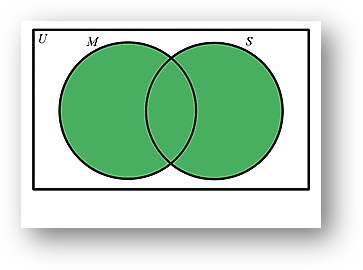
We are required to find |M ∪ S|
By using the formula, |M ∪ S| = |M| + |S| – |M ∩ S|
    |M ∪ S| = |M| + |S| – |M ∩ S|
                 = 70 + 40 – 10
                 = 100

Thus the number of students who study science or mathematics is 100.

Operations on Sets – Solved Examples

Problem 1: Let A = {1, 2, 3, 4, 5}, B = {3, 4, 5, 6, 7}, and C = {4, 5, 6, 7, 8}. Find (A △ B) ∩ (B △ C), where △ represents symmetric difference.

Solution:

First, let’s find A △ B:

A △ B = (A ∪ B) – (A ∩ B)

A ∪ B = {1, 2, 3, 4, 5, 6, 7}

A ∩ B = {3, 4, 5}

A △ B = {1, 2, 6, 7}

Now, let’s find B △ C:

B △ C = (B ∪ C) – (B ∩ C)

B ∪ C = {3, 4, 5, 6, 7, 8}

B ∩ C = {4, 5, 6, 7}

B △ C = {3, 8}

Finally, we find the intersection of these results:

(A △ B) ∩ (B △ C) = {1, 2, 6, 7} ∩ {3, 8} = ∅ (empty set)

Problem 2 : Given U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {1, 3, 5, 7, 9}, B = {2, 4, 6, 8}, and C = {1, 2, 3, 4, 5}.

Verify that (A ∪ B)’ = A’ ∩ B’, where ‘ denotes complement with respect to U.

Solution:

A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8, 9}

Find (A ∪ B)’:

(A ∪ B)’ = {10}

Find A’:

A’ = {2, 4, 6, 8, 10}

Find B’:

B’ = {1, 3, 5, 7, 9, 10}

Find A’ ∩ B’:

A’ ∩ B’ = {10}

Verify that (A ∪ B)’ = A’ ∩ B’:

Both sets equal {10}, so the equality holds.

Example 3 : Given sets A, B, and C, prove that A – (B ∪ C) = (A – B) ∩ (A – C).

Solution:

We’ll prove this by showing that an element x belongs to the left side if and only if it belongs to the right side.

Let x ∈ A – (B ∪ C)

This means x ∈ A and x ∉ (B ∪ C)

x ∉ (B ∪ C) implies x ∉ B and x ∉ C

Therefore:

x ∈ A and x ∉ B, so x ∈ (A – B)

x ∈ A and x ∉ C, so x ∈ (A – C)

Since x is in both (A – B) and (A – C), we can conclude:

x ∈ (A – B) ∩ (A – C)

Conversely, if x ∈ (A – B) ∩ (A – C):

x ∈ A and x ∉ B

x ∈ A and x ∉ C

This implies:

x ∈ A and x ∉ B and x ∉ C

Which is equivalent to: x ∈ A and x ∉ (B ∪ C)

Therefore, x ∈ A – (B ∪ C)

Thus, we’ve shown that an element belongs to A – (B ∪ C) if and only if it belongs to (A – B) ∩ (A – C), proving the equality.

Problem 4 : Cartesian Product and Power Set

Let A = {1, 2} and B = {a, b}. Find |P(A × B)|, where P denotes the power set and × denotes the Cartesian product.

Solution:

First, find A × B:

A × B = {(1,a), (1,b), (2,a), (2,b)}

|A × B| = 4

For any set S, |P(S)| = 2^|S|

Therefore, |P(A × B)| = 2^4 = 16

Problem 5 : Set Equality

Prove that (A – B) ∪ (B – A) = (A ∪ B) – (A ∩ B)

Solution:

Let x be an arbitrary element. We’ll show x is in the left side if and only if it’s in the right side.

x ∈ (A – B) ∪ (B – A)

⇔ x ∈ (A – B) or x ∈ (B – A)

⇔ (x ∈ A and x ∉ B) or (x ∈ B and x ∉ A)

⇔ (x ∈ A or x ∈ B) and (x ∉ A or x ∉ B)

⇔ x ∈ (A ∪ B) and x ∉ (A ∩ B)

⇔ x ∈ (A ∪ B) – (A ∩ B)

Thus, the two sets are equal.

Problem 6: Set Cardinality Let A and B be finite sets. Prove that |A ∪ B| = |A| + |B| – |A ∩ B|.

Solution:

Consider elements in A ∪ B:

Elements in A but not in B: |A| – |A ∩ B|

Elements in B but not in A: |B| – |A ∩ B|

Elements in both A and B: |A ∩ B|

Sum these up:

|A ∪ B| = (|A| – |A ∩ B|) + (|B| – |A ∩ B|) + |A ∩ B|

= |A| + |B| – |A ∩ B|

Problem 7 : Set Operations and Functions

Let f: A → B be a function. Prove that f(A – B) ⊆ f(A) – f(B) for any subset B of A.

Solution:

Let y ∈ f(A – B). We need to show y ∈ f(A) – f(B).

Since y ∈ f(A – B), there exists x ∈ A – B such that f(x) = y.

x ∈ A – B implies x ∈ A and x ∉ B.

Since x ∈ A, we know y = f(x) ∈ f(A).

We need to show y ∉ f(B). If y ∈ f(B), there would exist z ∈ B such that f(z) = y.

But f(z) = y = f(x), and x ∉ B. This contradicts x ∈ A – B.

Therefore, y ∈ f(A) and y ∉ f(B), so y ∈ f(A) – f(B).

Thus, f(A – B) ⊆ f(A) – f(B).

Problem 8: Principle of Inclusion-Exclusion ,For finite sets A, B, and C, prove:

|A ∪ B ∪ C| = |A| + |B| + |C| – |A ∩ B| – |B ∩ C| – |A ∩ C| + |A ∩ B ∩ C|

Solution:

Start with |A ∪ B ∪ C|.

Add |A|, |B|, and |C|. This counts elements in A, B, C, but overcounts elements in intersections.

Subtract |A ∩ B|, |B ∩ C|, and |A ∩ C| to correct for double counting.

However, elements in A ∩ B ∩ C have now been subtracted too many times, so add |A ∩ B ∩ C| back.

This gives the formula: |A ∪ B ∪ C| = |A| + |B| + |C| – |A ∩ B| – |B ∩ C| – |A ∩ C| + |A ∩ B ∩ C|

Problem 9: Countable and Uncountable Sets

Prove that the set of all infinite binary sequences is uncountable.

Solution:

We’ll use Cantor’s diagonalization argument:

Assume the set is countable. Then we can list all sequences:

s1: a11, a12, a13, …

s2: a21, a22, a23, …

s3: a31, a32, a33, …

…

Construct a new sequence t: t1, t2, t3, … where:

ti = 1 if aii = 0

ti = 0 if aii = 1

This new sequence t differs from every sequence in the list:

It differs from s1 in the 1st digit

It differs from s2 in the 2nd digit

It differs from s3 in the 3rd digit

…

Therefore, t is not in the list, contradicting our assumption that the list contained all sequences.

Thus, the set of all infinite binary sequences is uncountable.

Problem 10: Axiom of Choice

Using the Axiom of Choice, prove that every vector space has a basis.

Solution:

Let V be a vector space. Let S be the set of all linearly independent subsets of V.

Define a partial order ≤ on S by inclusion: A ≤ B if and only if A ⊆ B.

Let C be a chain in S (i.e., a totally ordered subset).

Let U = ∪{A : A ∈ C}. We claim U is an upper bound for C in S.

U is linearly independent: If not, some finite subset {u1, …, un} ⊆ U would be linearly dependent.

But each ui is in some Ai ∈ C, and since C is a chain, all ui are in the largest of these Ai.

This contradicts Ai being linearly independent.

By Zorn’s Lemma (equivalent to Axiom of Choice), S has a maximal element M.

M is a basis for V:

M is linearly independent by definition of S.

M spans V: If not, there exists v ∈ V not in span(M).

Then M ∪ {v} would be linearly independent and strictly larger than M, contradicting maximality.

Therefore, M is a basis for V.

Practice Problems on Operations on Sets

1. Let A = {1, 2, 3, 4, 5}, B = {2, 4, 6, 8}, and C = {3, 4, 5, 6}. Find:

• (A ∩ B) ∪ (B ∩ C)
• (A ∪ B) – C

2. If |A| = 5, |B| = 7, and |A ∪ B| = 10, find |A ∩ B|.

3. Prove or disprove: For any sets A, B, and C, (A – B) – C = A – (B ∪ C).

4. Let U be the universal set. Prove that for any sets A and B:

(A’ ∩ B’)’ = A ∪ B

5. If A and B are finite sets with |A| = m and |B| = n, Prove that:

|P(A) × P(B)| = 2^m+n

6. Let f: A → B be a function. Prove or disprove:

For any subsets X and Y of A, f(X ∩ Y) = f(X) ∩ f(Y)

7. Given that A, B, and C are sets, prove or disprove:

8. If A ⊆ B and B ⊆ C, then P(A) ⊆ P(B) ⊆ P(C)

9. Let A be a finite set with n elements. How many different pairs of subsets (X, Y) are there such that X ∪ Y = A

10. Let A be an infinite set and B be a finite set. Prove that |A| = |A – B|.

Summary

Set theory forms the foundation of modern mathematics, encompassing fundamental concepts like unions, intersections, complements, and Cartesian products. It deals with the properties of collections of objects, exploring relationships between sets through operations and identities. Key areas include understanding set cardinality, power sets, and the nuances of infinite sets. Set theory problems often involve proving equalities, working with functions on sets, and applying principles like inclusion-exclusion. These concepts are crucial in various mathematical fields and have practical applications in computer science, particularly in areas like database design and algorithm analysis. Mastering set theory requires a blend of logical reasoning, algebraic manipulation, and abstract thinking, providing a powerful toolset for tackling complex mathematical and computational challenges.

FAQs on Operations on Sets

How can operations be performed on sets?

In a set theory, there are three major types of operations performed on sets, such as:

• Union of sets (∪)
• Intersection of sets (∩)
• Difference of sets ( – )

What is the rule of set operations?

For two given sets A and B, A∪B (read as A union B) is the set of distinct elements that belong to set A and set B or both. The number of elements in A ∪ B is given by n(A∪B) = n(A) + n(B) − n(A∩B), where n(X) is the number of elements in set X.

Why are set operations important?

These operations are fundamental in set theory and are used to manipulate sets, define relationships between sets, and solve problems involving collections of objects. There are three major types of operations performed on sets, such as: Union of sets. Intersection of sets

What is associative law of set operation?

Associative law in sets asserts that grouping of sets when conducting set operations has no effect on the end output. In other words, it makes no difference how we arrange the sets; the result will be the same. We can better understand it by the example mentioned below: a ∪ ( b ∪ c ) = ( a ∪ b ) ∪ c.