Anand Classes offers clear and comprehensive NCERT Solutions for Exercise 10.1 of Chapter 10 Vector Algebra for Class 12 Mathematics, helping students understand the basics of vectors, direction ratios, and fundamental operations with step-by-step explanations. These notes are prepared according to the latest NCERT and CBSE guidelines, making them ideal for revision, concept building, and scoring high in board exams. Click the print button to download study material and notes.
NCERT Question.1 : Represent graphically a displacement of 40 km, 30° east of north.
Solution :
Let the displacement vector be $\overrightarrow{OA}$ such that
$$|\overrightarrow{OA}| = 40$$
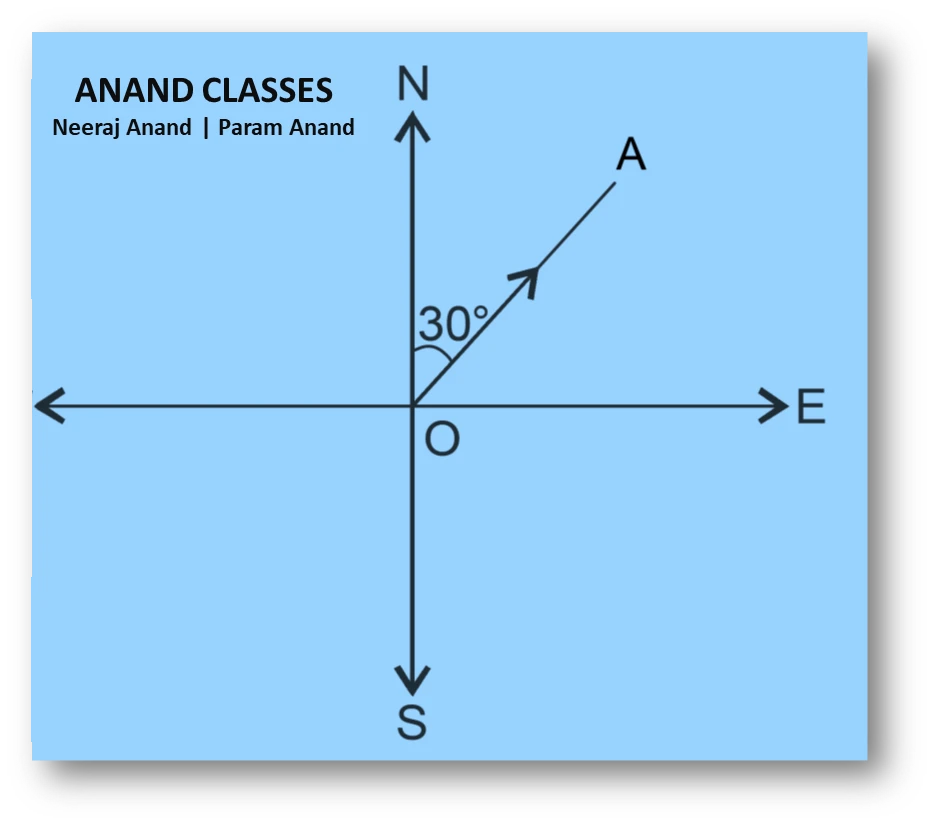
Displacement $40$km, $30^\circ$ East of North means the vector $\overrightarrow{OA}$ makes an angle $30^\circ$ with North in the East–North quadrant.
Note
“$\theta^\circ$ South of West’’ means a vector in the South–West quadrant making an angle of $\theta^\circ$ with West.
Download high-quality physics notes by Anand Classes, perfect for CBSE and competitive exams, with clear vector diagrams, solved examples, and concise explanations to strengthen your understanding.
NCERT Question.2 : Check the following measures as scalars and vectors.
(i) 10 kg (ii) 2 meters north-west (iii) 40° (iv) 40 Watt (v) 10– 19 coulomb (vi) 20 m/sec2.
Solution.
(i) 10 kg is a measure of mass and therefore a scalar (10 kg has no direction; it is magnitude only).
(ii) 2 meters North-West is a measure of displacement (has magnitude and direction both) and hence is a vector.
(iii) 40° is a measure of angle, i.e., magnitude only, and therefore a scalar.
(iv) 40 Watt is a measure of power (has no direction) and therefore a scalar.
(v) $10^{-19}$ coulomb is a measure of electric charge (is magnitude only) and therefore a scalar.
(vi) 20 m/sec2 is a measure of acceleration (rate of change of velocity) and hence is a vector.
Enhance your physics preparation with detailed notes and high-quality study material from Anand Classes, ideal for CBSE and competitive exams, offering clear conceptual explanations and well-structured solutions.
NCERT Question.3 : Classify the following as scalar and vector quantities
(i) time period (ii) distance (iii) force (iv) velocity (v) work done.
Solution :
(i) Time period – scalar
(ii) Distance – scalar
(iii) Force – vector
(iv) Velocity – vector
(v) Work done – scalar
(i) Time Period: Scalar (it measures duration and does not involve a direction).
(ii) Distance : Scalar (it measures the length of a path between two points and is directionless).
(iii) Force: Vector (it is described by both magnitude and the direction in which it acts).
(iv) Velocity: Vector (it represents the rate of change of position and includes direction).
(v) Work Done: Scalar (it is the energy transferred when a force is applied over a distance, but it does not inherently have a directional component).
Strengthen your physics concepts with well-structured notes and solved examples from Anand Classes, ideal for CBSE and competitive exam preparation, offering clear explanations and student-friendly learning material.
NCERT Question.4 : In the adjoining figure (a square), identify the following vectors
(i) co-initial
(ii) equal
(iii) collinear but not equal
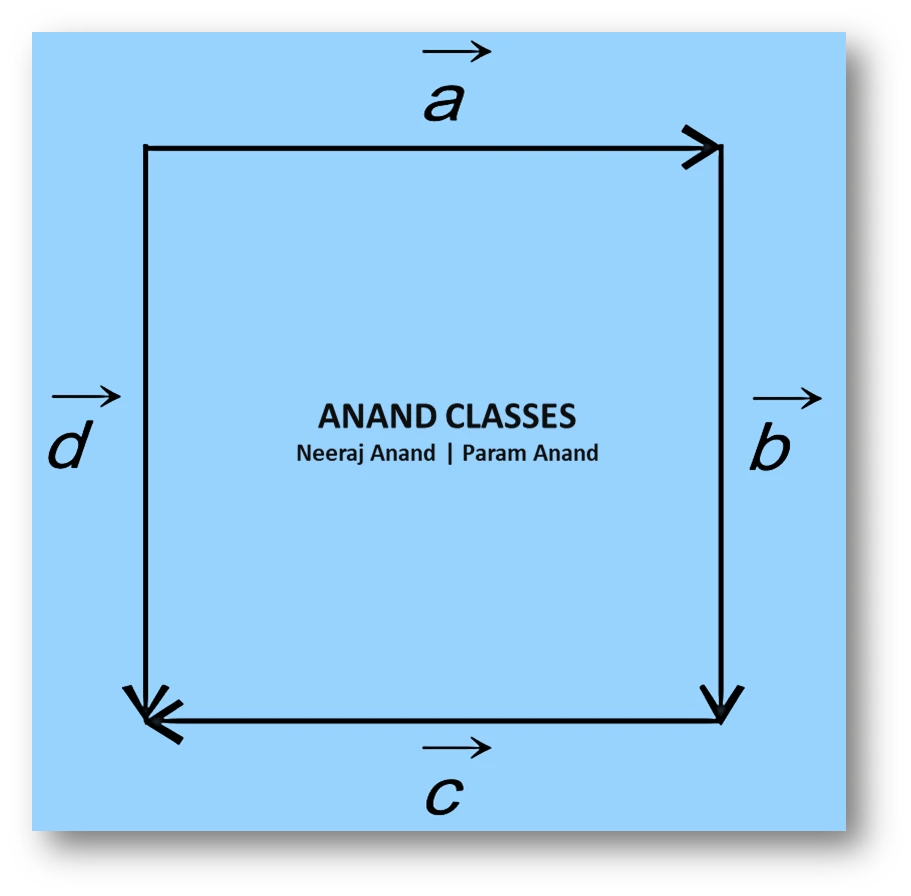
Solution :
- $\vec{a}$ and $\vec{d}$ have the same initial point and therefore are co-initial vectors.
- $\vec{b}$ and $\vec{d}$ have the same direction and the same magnitude. Therefore, $\vec{b}$ and $\vec{d}$ are equal vectors.
- $\vec{a}$ and $\vec{c}$ have parallel supports, so they are collinear. Since they have opposite directions, they are not equal. Hence, $\vec{a}$ and $\vec{c}$ are collinear but not equal.
Access structured vector notes, diagrams, and chapter-wise solved examples from Anand Classes, perfect for CBSE and competitive exam preparation, designed to build strong fundamentals with clear and concise explanations.
NCERT Question.5 : Answer the following as true or false
(i) $\vec{a}$ and $-\vec{a}$ are collinear.
(ii) Two collinear vectors are always equal in magnitude.
(iii) Two vectors having same magnitude are collinear.
(iv) Two collinear vectors having the same magnitude are equal.
Solution :
(i) True
$\vec{a}$ and $-\vec{a}$ are collinear because they lie on the same line and these vectors have same magnitude but opposite in direction.
Collinear vectors are vectors that are parallel to the same line or lie on the same line, meaning they point in the same or opposite directions. Two vectors are collinear if one is a scalar multiple of the other, i.e., $\vec{a}=\lambda\vec{b}$ where λ is a scalar. Here λ =-1.
(ii) False
Collinear vectors must be aligned along the same line, but they can have different magnitudes.
$\vec{A}$ and $2\vec{A}$ are collinear but
$$|\vec{A}| \neq 2|\vec{A}|$$
so their magnitudes are not always equal.
(iii) False
Having the same magnitude does not imply that vectors are collinear.
$$|\hat{i}| = |\hat{j}| = 1$$
but $\hat{i}$ is along the x–axis and $\hat{j}$ is along the y–axis.
They are not collinear.
(iv) False
This statement is not necessarily true because two collinear vectors of the same magnitude can point in opposite directions.
Vectors $\vec{A}$ and $-\vec{A}$ have the same magnitude but opposite directions.
Hence, they are not equal.
Note :
Two vectors $\vec{A}$ and $\vec{B}$ are equal if they have same magnitude and same direction, that is :
(i) $|\vec{A}| = |\vec{B}|$
(ii) They have the same direction.
Prepare effectively with concise vector notes, solved examples, and high-quality study material from Anand Classes, ideal for CBSE and competitive exams such as JEE, NDA to strengthen conceptual understanding.

