Resonance and Resonance Energy, Characteristics, Conditions, Examples, Bond Order in Resonance

Anand Classes provides complete Class 11 Chemistry notes on Resonance and Resonance Energy with definitions, characteristics, conditions, examples, and bond order in resonance structures. Learn how the delocalization of electrons leads to multiple contributing structures, understand the stability of molecules through resonance energy, and master key formulas and solved MCQs for NEET, JEE, and CBSE exams. These well-structured notes are perfect for quick revision and concept clarity. Click the print button to download study material and notes.

What is Resonance?

The phenomenon of resonance was put forward by Heisenberg to explain the properties of certain molecules.

Often, a single Lewis structure is not adequate to represent a molecule in agreement with its experimentally determined parameters.

Example: Ozone ($O_3$)

In this case, each oxygen atom has an octet of electrons. According to this structure, there is one single bond (O – O) and one double bond (O = O) in the molecule. The normal O–O and O=O bond lengths are 148 pm and 121 pm respectively.

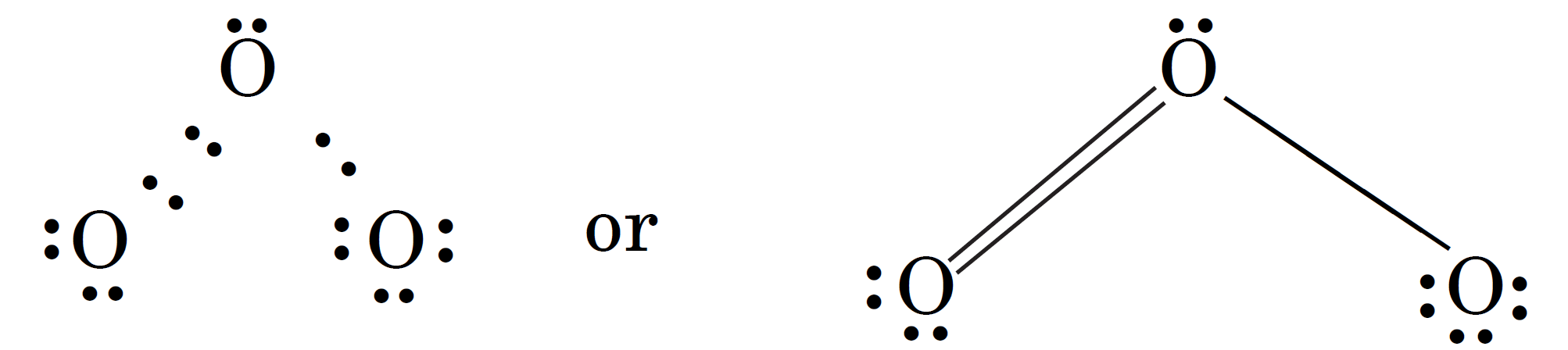
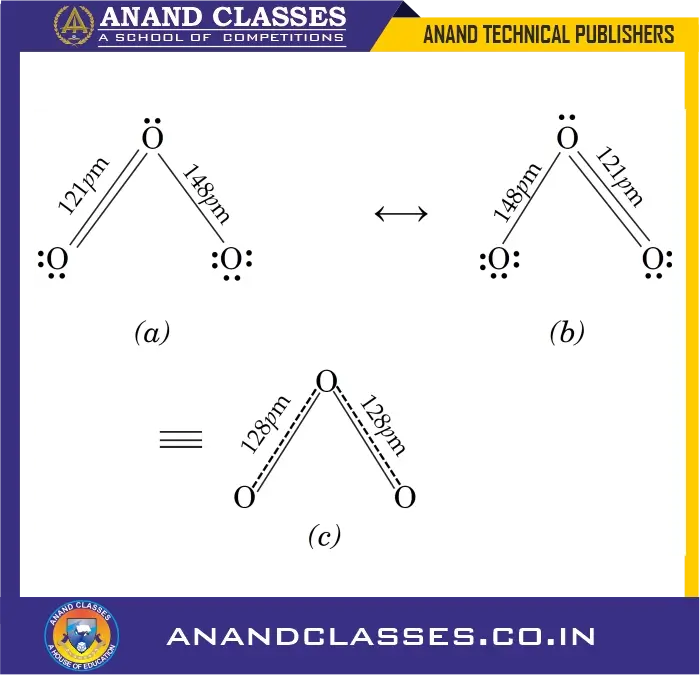
According to the above structure we would expect the two bond lengths in ozone molecule to be unequal. However, experimentally it is observed that both the bond lengths are equal (128 pm) and the bonds are intermediate between single and double bonds. This means that the above Lewis structure does not account for the observed experimental facts. To solve the problem, an alternative structure may be drawn as :

In this case, the double bond and the single bond are interchanged. But none of these two structures explains the observed facts. It is proposed that the actual structure is in between the two structures.

In such a case, we say that the actual structure is a resonance hybrid of these two structures. The individual structures are called resonance structures or contributing structures. These are represented by drawing double headed arrows between these structures as shown below :

Definition:
Thus, resonance may be defined as when a molecule cannot be represented by a single structure but its properties can be described by two or more structures, the actual structure is called a resonance hybrid. The individual structures are resonance structures (contributing structures), shown with a double-headed arrow ($\leftrightarrow$).

For example, ozone molecule may be represented as a resonance hybrid of above two structures (a) and (b). For simplicity, ozone may be represented by structure (c) which shows the resonance hybrid having equal bonds between single and double.

What are the Conditions for Writing Resonance Structures?

The following are essential conditions for writing resonating structures :

1. The contributing structures should have same atomic positions.
2. The contributing structures should have same number of unpaired electrons.
3. The contributing structures should have nearly same energy.
4. The structures should be so written that negative charge is present on an electronegative atom and positive charge is present on an electropositive atom.
5. In contributing structures, the like charges should not reside on adjacent atoms.
   The contributing structures should not differ much in energy. This is an important condition. The individual structures of similar energy contribute equally to the resonance hybrid.

Examples of Resonance

(i) Carbon dioxide (CO₂) molecule

The simple structure of carbon dioxide molecule is :

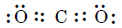
Therefore, we expect a double bond between carbon and oxygen atoms. The experimentally determined carbon to oxygen bond length in CO₂ molecule is 115 pm.

The normal $C=O$ bond length is 122 pm and $C \equiv O$ bond length is 110 pm. This suggests that carbon-oxygen bond in CO₂ molecule is between double and triple bond.
Obviously, a single structure cannot depict the true structure of the molecule and it becomes necessary to write more than one Lewis structures. Therefore, the structure of CO₂ is best described as a resonance hybrid of the following three canonical forms :

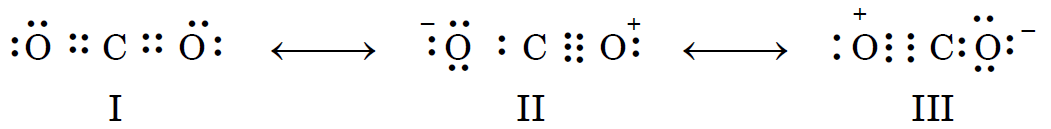
(ii) Carbon monoxide (CO) molecule

• Lewis structure suggests a double bond.

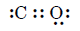
• Experimental bond length = 113 pm (between $C=O$ 122 pm and $C \equiv O$ 110 pm).

Therefore, $CO$ is a resonance hybrid of multiple canonical forms.

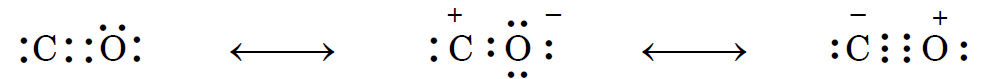
Resonating Structures and resonance hybrid of Carbon monoxide (CO) molecule

What are the Effects of Resonance?

• Resonance averages the bond characteristics of a molecule.
• Resonance stabilizes the molecule since resonance hybrid energy is less than the energy of any canonical form.

What is Resonance Energy?

Definition:
The difference between the actual bond energy of the molecule and that of the most stable resonating structure.

$$
\text{Resonance energy} = E_{\text{actual}} – E_{\text{most stable structure}}
$$

For example, the resonance energy of carbon dioxide is 138 kJ/mol. This means that the actual molecule of CO₂ is about 138 kJ more stable than the most stable structure among the contributing structures. This can be easily illustrated as given below :

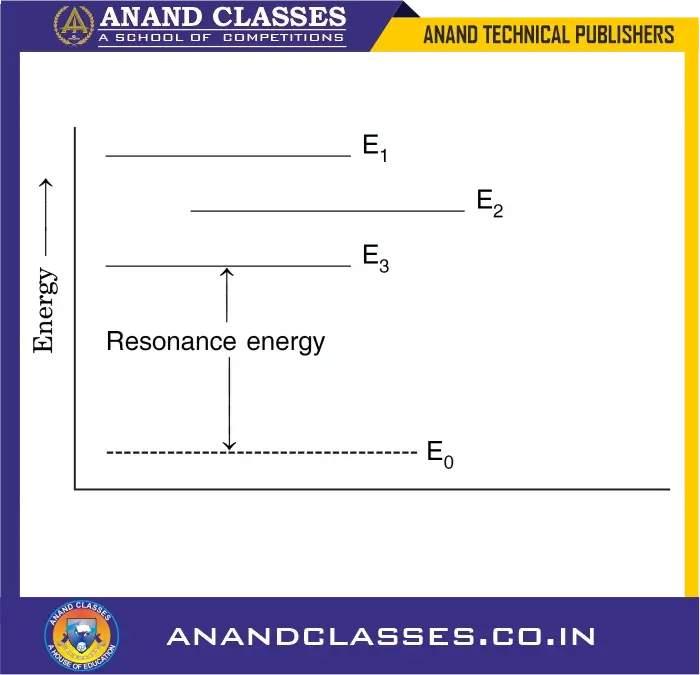
Suppose E₁, E₂ and E₃ are the energies of three resonating structures for a molecule. Their energies are shown in diagram. It is evident that among these, E₃ has the lowest energy (most stable contributing structure). If E₀ is the actual energy of the molecule (experimentally determined), then resonance energy is E₃ – E₀.

Characteristics of Resonance

1. Contributing structures have no real existence; only the resonance hybrid exists.
2. Resonance makes bond lengths equal.
   • In $O_3$, both $O—O$ bonds are equal.
   • In benzene, all $C—C$ bonds are equal.
3. Resonance hybrid has lower energy and higher stability.
4. Greater resonance energy → greater stability.
5. Resonance is a theoretical concept.

How to Calculate Bond Order in Resonance?

Bond order is averaged over contributing structures:

$$
\text{Bond order} = \frac{\text{Total number of bonds between two atoms in all structures}}{\text{Total number of resonating structures}}
$$

Any two bonded atoms may be selected and a double bond is counted as 2 bonds and a triple bond is counted as 3 bonds.

Examples:

• Benzene ($C_6H_6$):
  Between two carbons, one structure has a double bond (2), another has a single bond (1).

$$
\text{Bond order} = \frac{2 + 1}{2} = 1.5
$$

• Carbonate ion ($CO_3^{2-}$):
  Has three equivalent resonance structures.

$$
\text{Bond order} = \frac{2 + 1 + 1}{3} = 1.33
$$

Common Misconceptions about Resonance

1. Resonance structures (canonical forms) have no real existence.
2. A molecule does not spend part of the time in one form and part in another.
3. There is no equilibrium between canonical forms (unlike tautomerism).
4. The real molecule cannot be represented by a single Lewis structure.

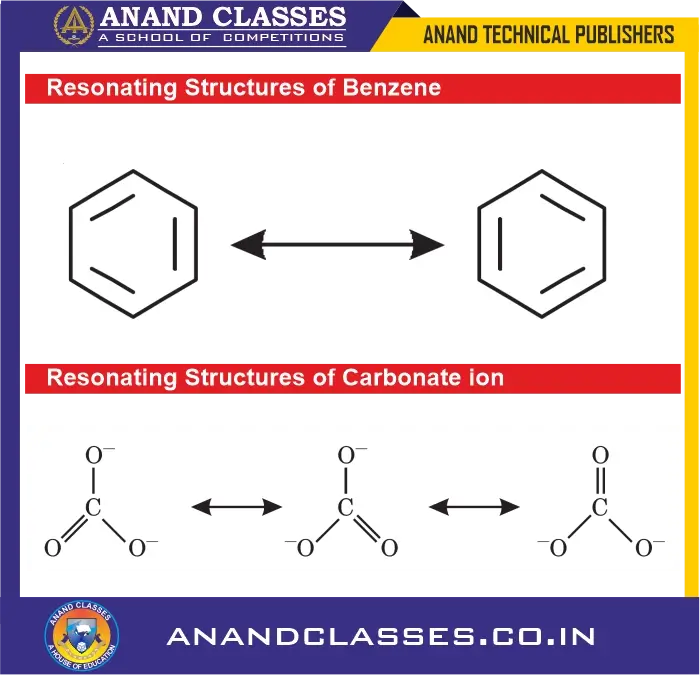
Resonance structures of important molecules and ions

The resonance structures of a few more molecules and ions are given ahead.

Short Answer Conceptual Questions (SAT)

Q1. Define resonance. Give an example.

Answer:
Resonance is the phenomenon in which a molecule cannot be represented by a single Lewis structure, but its properties can be explained by two or more structures. The actual structure is a resonance hybrid.
Example: Ozone ($O_3$). Both O—O bonds are equal in length (128 pm), intermediate between single (148 pm) and double (121 pm) bonds.

Q2. What is resonance energy?

Answer:
Resonance energy is the difference between the actual energy of a molecule and the energy of its most stable canonical form.
Example: Resonance energy of $CO_2$ is 138 kJ mol$^{-1}$.

Q3. Why are all $C–C$ bonds in benzene equal?

Answer:
Because benzene is a resonance hybrid of two structures. Resonance makes all bond lengths equal, hence each $C–C$ bond length = 139 pm.

Multiple Choice Questions (MCQs)

Q1. Which molecule shows resonance?
(a) $H_2O$
(b) $CO_2$
(c) $NH_3$
(d) $CH_4$

Answer: (b) $CO_2$
Explanation: Bond length of $CO_2$ (115 pm) is intermediate between $C=O$ (122 pm) and $C \equiv O$ (110 pm), hence resonance occurs.

Q2. The bond order of each $C–O$ bond in carbonate ion $CO_3^{2-}$ is:
(a) 1.0
(b) 1.5
(c) 1.33
(d) 2.0

Answer: (c) 1.33
Explanation:
Bond order $= \dfrac{2+1+1}{3} = 1.33$.

Q3. Resonance stabilizes a molecule because:
(a) It decreases bond order
(b) It increases bond energy
(c) Resonance hybrid has higher energy than canonical forms
(d) Resonance makes molecules less stable

Answer: (b) It increases bond energy
Explanation: Resonance lowers overall energy, increases bond energy, and stabilizes the molecule.

Assertion-Reason Questions

Q1.
Assertion (A): All O—O bonds in ozone are equal.
Reason (R): Ozone molecule is a resonance hybrid of two canonical forms.

• (a) A and R both true, R is correct explanation of A
• (b) A and R both true, R is not correct explanation of A
• (c) A true, R false
• (d) A false, R true

Answer: (a)
Explanation: Resonance equalizes bond lengths, hence all O—O bonds in ozone are equal.

Q2.
Assertion (A): Resonance energy is always positive.
Reason (R): The resonance hybrid is always more stable than any canonical form.

Answer: (a)
Explanation: By definition, resonance stabilizes the molecule, so resonance energy is positive.

Case Study Question

Read the following passage and answer the questions:

Benzene is represented by two Kekulé structures. Each Kekulé structure has alternating single and double bonds between carbon atoms. However, experimentally, all $C–C$ bond lengths in benzene are equal (139 pm). The heat of hydrogenation of benzene is much less than the expected value if it had three isolated double bonds. This extra stability is called resonance energy.

Q1. Why are all $C–C$ bonds equal in benzene?
Answer: Because benzene is a resonance hybrid of two Kekulé structures, resonance equalizes all bond lengths.

Q2. What is the bond order of each $C–C$ bond in benzene?
Answer:
Bond order $= \dfrac{2+1}{2} = 1.5$

Q3. Define resonance energy in context of benzene.
Answer: Resonance energy is the stabilization energy due to delocalization of electrons. In benzene, the actual heat of hydrogenation is less than expected, indicating extra stability.