Anand Classes presents a complete and free-downloadable PDF of NCERT-Solutions for Class 11 Maths Chapter 2 (Relations and Functions) Exercise 2.2 prepared to aid students in understanding relations, domain, range and codomain with clarity. Dive into detailed explanations and methodical answers that align with the latest CBSE syllabus. Click the print button to download study material and notes.
NCERT Problem 1 : Let $A = \{1, 2, 3, \ldots, 14\}$. Define a relation $R$ from $A$ to $A$ by
$$R = \{(x, y) : 3x – y = 0,; x, y \in A\}.$$
Write down its domain, codomain, and range.
Solution :
Given:
$$A = \{1, 2, 3, \ldots, 14\}$$
and
$$R = \{(x, y) : 3x – y = 0\} \Rightarrow y = 3x$$
Now find the ordered pairs such that $x, y \in A$:
- For $x = 1$, $y = 3(1) = 3 \in A$
- For $x = 2$, $y = 3(2) = 6 \in A$
- For $x = 3$, $y = 3(3) = 9 \in A$
- For $x = 4$, $y = 3(4) = 12 \in A$
- For $x = 5$, $y = 3(5) = 15 \notin A$
Thus,
$$R = \{(1, 3), (2, 6), (3, 9), (4, 12)\}$$
Domain
The set of all first elements:
$$\text{Domain}(R) = \{1, 2, 3, 4\}$$
Codomain
The entire set $A$:
$$\text{Codomain}(R) = \{1, 2, 3, \ldots, 14\}$$
Range
The set of all second elements:
$$\text{Range}(R) = \{3, 6, 9, 12\}$$
Download expert-designed Relations and Functions NCERT solutions by Anand Classes — perfect for CBSE Class 11 Maths exam success.
NCERT Problem 2 : Define a relation $R$ on the set $\mathbb{N}$ of natural numbers by
$R = \{(x, y) : y = x + 5, \\[1em] x \text{ is a natural number less than } 4 \;\|\; x, y \in \mathbb{N}\}.$
Depict this relation using roster form. Write down the domain and the range.
Solution :
Natural numbers less than $4$ are: $1, 2, 3$
So,
$$R = \{(x, y) : y = x + 5\} = \{(1, 6), (2, 7), (3, 8)\}$$
Domain
The domain of $R$ is the set of all first elements:
$$\text{Domain}(R) = \{1, 2, 3\}$$
Range
The range of $R$ is the set of all second elements:
$$\text{Range}(R) = \{6, 7, 8\}$$
Download Class 11 Relations and Functions notes and NCERT solutions by Anand Classes — perfect for CBSE Maths preparation.
NCERT Problem 3 : Let $A = \{1, 2, 3, 5\}$ and $B = \{4, 6, 9\}$. Define a relation $R$ from $A$ to $B$ by
$R = \{(x, y) : \text{the difference between } x \text{ and } y \text{ is odd},\\[1em] \;| \; x \in A, y \in B\}.$
Write $R$ in roster form.
Solution :
We check each pair $(x, y)$ such that $x \in A$ and $y \in B$ and include those where $|x – y|$ is odd.
Thus, the relation is:
$$R = \{(1,4), (1,6), (2,9), (3,4), (3,6), (5,4), (5,6)\}$$
Get Class 11 Relations and Functions printable notes and NCERT solutions by Anand Classes — best for CBSE exam preparation.
NCERT Problem 4 : Figure shows a relationship between the sets $P$ and $Q$. Write this relation:
(i) in set-builder form
(ii) in roster form
Also give its domain and range.
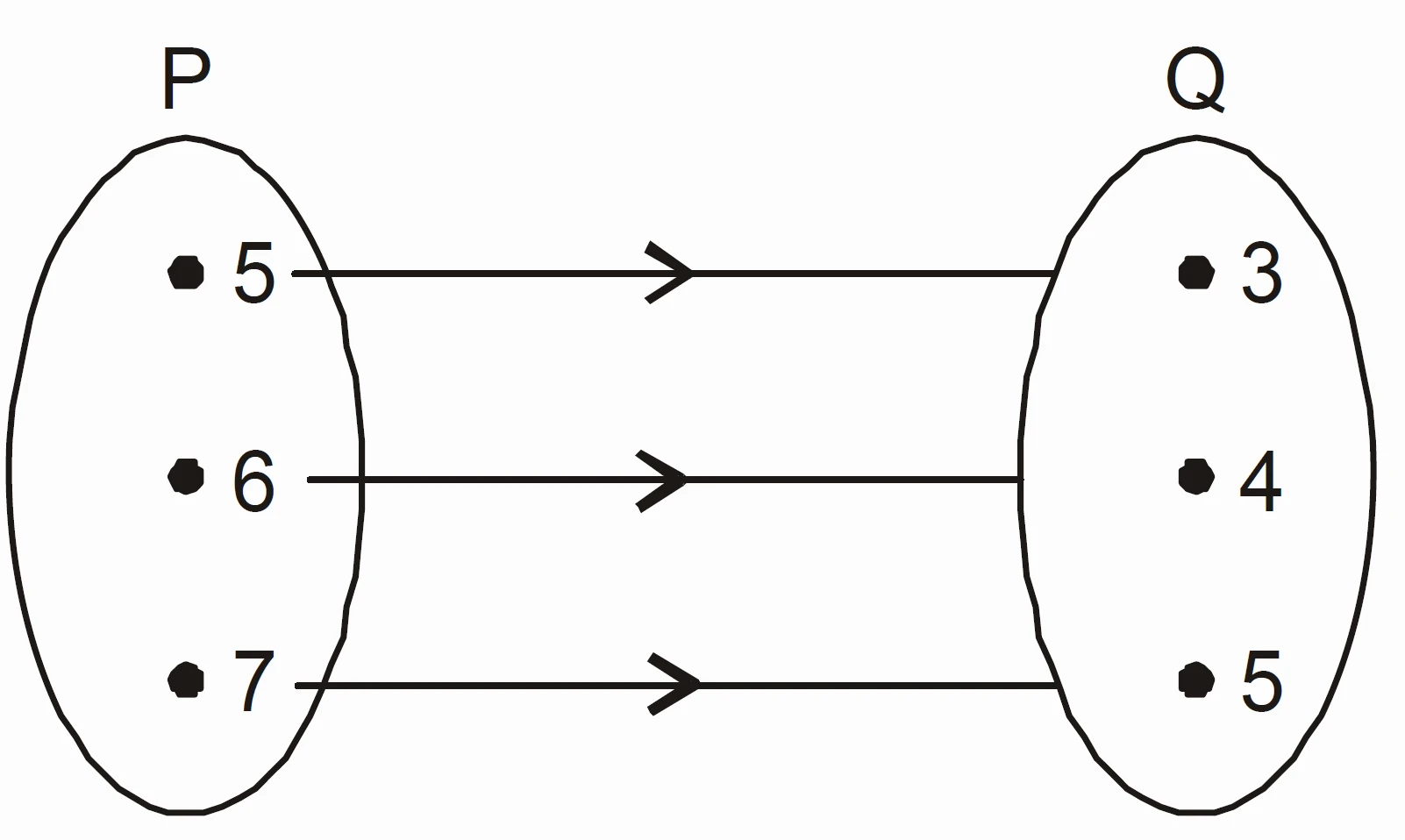
Solution :
From the figure:
$$P = \{5, 6, 7\}, \quad Q = \{3, 4, 5\}$$
The relation shown is:
- $5$ is related to $3$
- $6$ is related to $4$
- $7$ is related to $5$
(i) Set-builder Form
$$R = \{(x, y) : y = x – 2, x \in P\}$$
(ii) Roster Form
$$R = \{(5, 3), (6, 4), (7, 5)\}$$
Domain
The set of all first elements:
$$\text{Domain}(R) = \{5, 6, 7\}$$
Range
The set of all second elements:
$$\text{Range}(R) = \{3, 4, 5\}$$
Download complete Relations and Functions Class 11 NCERT solutions and notes by Anand Classes — ideal for CBSE exam scoring.
NCERT Problem 5 : Let $A = \{1, 2, 3, 4, 6\}$. Let $R$ be the relation on $A$ defined by:
$R = \{(a, b) : a, b \in A, \;|\; b \text{ is exactly divisible by } a\}.$
(i) Write $R$ in roster form.
(ii) Find the domain of $R$.
(iii) Find the range of $R$.
Solution :
Given:
$$A = \{1, 2, 3, 4, 6\}$$
and
$$R = \{(a, b) : b \text{ is exactly divisible by } a\}$$
(i) Roster Form
Check divisibility within set $A$:
- $1$ divides all elements
- $2$ divides $2, 4, 6$
- $3$ divides $3, 6$
- $4$ divides $4$
- $6$ divides $6$
Thus,
$R = \{(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), \\[1em](3, 3), (3, 6), (4, 4), (6, 6)\}$
(ii) Domain
All first elements:
$$\text{Domain}(R) = \{1, 2, 3, 4, 6\}$$
(iii) Range
All second elements:
$$\text{Range}(R) = \{1, 2, 3, 4, 6\}$$
Strengthen your CBSE Class 11 Maths Relations and Functions understanding with expert NCERT solutions by Anand Classes — perfect for exam success.
NCERT Problem 6 : Determine the domain and range of the relation $R$ defined by
$$R = \{(x, x + 5) : x \in {0, 1, 2, 3, 4, 5}\}$$
Solution :
Here, the relation $R$ is given by,
$$R = \{(x, x + 5) : x \in \{0, 1, 2, 3, 4, 5\}\}$$
So, relation
$$R = \{(0,5), (1,6), (2,7), (3,8), (4,9), (5,10)\}$$
Now, we know that the domain of a relation $R$ is the set of all the first elements of the ordered pairs in the relation.
So,
$$\text{Domain of } R = \{0, 1, 2, 3, 4, 5\}$$
Now, we know that the range of a relation $R$ is the set of all the second elements of the ordered pairs in the relation.
So,
$$\text{Range of } R = \{5, 6, 7, 8, 9, 10\}$$
NCERT Problem 7 : Write the relation
$R = \{(x, x^3) : x \text{ is a prime number less than } 10\}$ in roster form.
Solution :
Here, the relation $R$ is given by,
$$R = \{(x, x^3) : x \text{ is a prime number less than } 10\}$$
As we know, the prime numbers less than $10$ are $2, 3, 5,$ and $7$.
So, the relation
$$R = \{(2, 8), (3, 27), (5, 125), (7, 343)\}$$
NCERT Problem 8 : Let $A = \{x, y, z\}$ and $B = \{1, 2\}$. Find the number of relations from $A$ to $B$.
Solution :
Given,
$A = \{x, y, z\}$ and $B = \{1, 2\}$
Number of elements in set $A$ is:
$$n(A) = 3$$
Number of elements in set $B$ is:
$$n(B) = 2$$
So,
$$n(A \times B) = n(A) \times n(B) = 3 \times 2 = 6$$
We know that the number of relations from $A$ to $B$ is given by:
$$2^{n(A \times B)} = 2^6 = 64$$
OR
$A = \{x, y, z\}$ and $B = \{1, 2\}$
Then,
$$A \times B = \{(x,1), (x,2), (y,1), (y,2), (z,1), (z,2)\}$$
Number of ordered pairs:
$$n(A \times B) = 6$$
So,
$$\text{Number of subsets of } A \times B = 2^6 = 64$$
Thus, the number of relations from $A$ to $B$ is $64$.
Perfect for CBSE and JEE aspirants — study material by Anand Classes helps build strong mathematics fundamentals.
Click the print button to download study material and notes.
NCERT Problem 9 : Let $R$ be the relation on $\mathbb{Z}$ defined by
$R = \{(a,b) : a, b \in \mathbb{Z}, a – b \text{ is an integer}\}$
Find the domain and range of $R$.
Solution :
The relation is given by:
$$R = \{(a, b) : a, b \in \mathbb{Z}, a – b \in \mathbb{Z}\}$$
Since the difference between any two integers is always an integer, the condition is satisfied for all integer pairs.
Therefore,
- Domain of $R = \mathbb{Z}$
- Range of $R = \mathbb{Z}$
Boost your Class 11 Math preparation with expertly formatted solutions by Anand Classes — ideal for CBSE and competitive exams.
Summary
Exercise 2.2 of Chapter 2 “Relations and Functions” in the Class 11 NCERT Mathematics textbook explores the concepts of different types of functions, including injective (one-to-one), surjective (onto), and bijective functions. The exercise provides practice problems that help students understand how to determine and prove these properties. It emphasizes the importance of understanding these fundamental concepts, which are essential for higher-level mathematics and real-world applications. Through this exercise, students learn to analyze functions and their properties, building a strong foundation for advanced topics in mathematics.


