Inverse trigonometric functions are the inverse functions of the trigonometric ratios i.e. sin, cos, tan, cot, sec, cosec. These functions are widely used in fields like physics, mathematics, engineering and other research fields.
Table of Contents
There are two popular notations used for inverse trigonometric functions:
Adding “arc” as a prefix.
Example: arcsin(x), arccos(x), arctan(x), …
Adding “-1” as superscript.
Example: sin-1(x), cos-1(x), tan-1(x), …
In this article, we will learn about graphs and nature of various inverse functions.
Inverse of Sine Function, y = sin-1(x)
sin-1(x) is the inverse function of sin(x). Its domain is [−1, 1] and its range is [- π/2, π/2]. It intersects the coordinate axis at (0,0). It is an odd function and is strictly increasing in (-1, 1).
Graph of Function
![Graphs of Inverse Trigonometric Functions-Formulas, Solved Examples, Class 12 Math Chapter 2 Notes Study Material Download free pdf Graph of Sin-1(x). sin-1(x) is the inverse function of sin(x). Its domain is [−1, 1] and its range is [- π/2, π/2]. It intersects the coordinate axis at (0,0). It is an odd function and is strictly increasing in (-1, 1).](https://anandclasses.in/wp-content/uploads/2025/08/46.png)
Graph of Sin-1(x)
Function Analysis
| Domain | x∈[−1,1]x∈[−1,1] |
|---|---|
| Range | y∈[−π2,π2]y∈[2−π,2π] |
| X – Intercept | x=0x=0 |
| Y – Intercept | y=0y=0 |
| Minima | (−1,−π2)(−1,2−π) |
| Maxima | (1,π2)(1,2π) |
| Inflection Points | (0,0)(0,0) |
| Parity | Odd Function |
| Monotonicity | In (-1, 1) strictly increasing |
Sample Problems on Inverse Sine Function
Problem 1: Find the principal value of the given equation:
y = sin-1(1/√2)
Solution:
We are given that:
y = sin-1(1/√2)
So we can say that,
sin(y) = (1/√2)
We know that the range of the principal value branch of sin-1(x) is (−π/2, π/2) and sin(π/4) = 1/√2.
So, the principal value of sin-1(1/√2) = π/4.
Problem 2: Find the principal value of the given equation:
y = sin-1(1)
Solution:
We are given that:
y = sin-1(1)
So we can say that,
sin(y) = 1
We know that the range of the principal value branch of sin-1(x) is (−π/2, π/2) and sin(π/2) = 1.
So, the principal value of sin-1(1) = π/2.
Inverse of Cosine Function, y = cos-1(x)
cos-1(x) is the inverse function of cos(x). Its domain is [−1, 1] and its range is [0, π]. It intersects the coordinate axis at (1, π/2). It is neither even nor an odd function and is strictly decreasing in (-1, 1).
Graph of Function
![Graphs of Inverse Trigonometric Functions-Formulas, Solved Examples, Class 12 Math Chapter 2 Notes Study Material Download free pdf cos-1(x) is the inverse function of cos(x). Its domain is [−1, 1] and its range is [0, π]. It intersects the coordinate axis at (1, π/2). It is neither even nor an odd function and is strictly decreasing in (-1, 1).](https://anandclasses.in/wp-content/uploads/2025/08/47.png)
Graph of Cos-1(x)
Function Analysis
| Domain | x∈[−1,1]x∈[−1,1] |
|---|---|
| Range | y∈[0,π]y∈[0,π] |
| X – Intercept | x=1x=1 |
| Y – Intercept | y=π2y=2π |
| Minima | (1,0)(1,0) |
| Maxima | (−1,π)(−1,π) |
| Inflection Points | (0,π2)(0,2π) |
| Parity | Neither Even Nor Odd |
| Monotonicity | In (-1, 1) strictly decreasing |
Sample Problems on Inverse Cosine Function
Problem 1: Find the principal value of the given equation:
y = cos-1(1/√2)
Solution:
We are given that:
y = cos-1(1/√2)
So we can say that,
cos(y) = (1/√2)
We know that the range of the principal value branch of cos-1(x) is (0, π) and cos(π/4) = 1/√2.
So, the principal value of cos-1(1/√2) = π/4.
Problem 2: Find the principal value of the given equation:
y = cos-1(1)
Solution:
We are given that:
y = cos-1(1)
So we can say that,
cos(y) = 1
We know that the range of the principal value branch of cos-1(x) is (0, π) and cos(0) = 1.
So, the principal value of cos-1(1) = 0.
Inverse of Tangent Function, y = tan-1(x)
tan-1(x) is the inverse function of tan(x). Its domain is ℝ and its range is [-π/2, π/2]. It intersects the coordinate axis at (0, 0). It is an odd function which is strictly increasing in (-∞, ∞).
Graph of Function
![Graphs of Inverse Trigonometric Functions-Formulas, Solved Examples, Class 12 Math Chapter 2 Notes Study Material Download free pdf tan-1(x) is the inverse function of tan(x). Its domain is ℝ and its range is [-π/2, π/2]. It intersects the coordinate axis at (0, 0). It is an odd function which is strictly increasing in (-∞, ∞).](https://anandclasses.in/wp-content/uploads/2025/08/48.png)
Graph of tan-1(x)
Function Analysis
| Domain | x∈Rx∈R |
|---|---|
| Range | y∈(−π2,π2)y∈(2−π,2π) |
| X – Intercept | x=0x=0 |
| Y – Intercept | y=0y=0 |
| Minima | The function does not have any minima points. |
| Maxima | The function does not have any maxima points. |
| Inflection Points | (0,0)(0,0) |
| Parity | Odd Function |
| Monotonicity | In (−∞, ∞) strictly Increasing |
| Asymptotes | y=π2 and y=−π2y=2π and y=2−π |
Sample Problems on Inverse of Tangent Function
Problem 1: Find the principal value of the given equation:
y = tan-1(1)
Solution:
We are given that:
y = tan-1(1)
So we can say that,
tan(y) = (1)
We know that the range of the principal value branch of tan-1(x) is (-π/2, π/2) and tan(π/4) = 1.
So, the principal value of tan-1(1) = π/4.
Problem 2: Find the principal value of the given equation:
y = tan-1(√3)
Solution:
We are given that:
y = tan-1(√3)
So we can say that,
tan(y) = (√3)
We know that the range of the principal value branch of tan-1(x) is (-π/2, π/2) and tan(π/3) = √3.
So, the principal value of tan-1(√3) = π/3.
Inverse of Cosecant Function, y = cosec-1(x)
cosec-1(x) is the inverse function of cosec(x). Its domain is (-∞, -1] U [1, ∞) and its range is [-π/2, 0) U (0, π/2]. It doesn’t intercept the coordinate axis. It is an odd function that is strictly decreasing in its domain.
Graph of Function
![Graphs of Inverse Trigonometric Functions-Formulas, Solved Examples, Class 12 Math Chapter 2 Notes Study Material Download free pdf cosec-1(x) is the inverse function of cosec(x). Its domain is (-∞, -1] U [1, ∞) and its range is [-π/2, 0) U (0, π/2]. It doesn’t intercept the coordinate axis. It is an odd function that is strictly decreasing in its domain.](https://anandclasses.in/wp-content/uploads/2025/08/49.png)
Graph of Cosec-1(x)
Function Analysis
| Domain | x∈(−∞,−1]∪[1,∞)x∈(−∞,−1]∪[1,∞) |
|---|---|
| Range | y∈[−π2,0)∪(0,π2]y∈[2−π,0)∪(0,2π] |
| X – Intercept | ϕϕ |
| Y – Intercept | ϕϕ |
| Minima | (−1,−π2)(−1,2−π) |
| Maxima | (1,π2)(1,2π) |
| Inflection Points | The function does not have any inflection points. |
| Parity | Odd Function |
| Monotonicity | In (1, ∞) it is decreasing and in (-∞, -1) it is decreasing |
| Asymptotes | y = 0 |
Sample Problems on Inverse Cosecant Function
Problem 1: Find the principal value of the given equation:
y = cosec-1(√2)
Solution:
We are given that:
y = cosec-1(√2)
So we can say that,
cosec(y) = (√2)
We know that the range of the principal value branch of cosec-1(x) is [-π/2, π/2] – {0} and cosec(π/4) = √2.
So, the principal value of cosec-1(√2) = π/4.
Problem 2: Find the principal value of the given equation:
y = cosec-1(1)
Solution:
We are given that:
y = cosec-1(√2)
So we can say that,
cosec(y) = 1
We know that the range of the principal value branch of cosec-1(x) is [-π/2, π/2] – {0} and cosec(π/2) = 1.
So, the principal value of cosec-1(1) = π/2.
Inverse of Secant Function, y = sec-1(x)
sec-1(x) is the inverse function of sec(x). Its domain is (-∞, -1] U [1, ∞) and its range is [0, π/2) U (π/2, π]. It doesn’t intercept the coordinate axis as it is a discontinuous function. It is neither even nor odd function and is strictly increasing in its domain.
Graph of Function
![Graphs of Inverse Trigonometric Functions-Formulas, Solved Examples, Class 12 Math Chapter 2 Notes Study Material Download free pdf sec-1(x) is the inverse function of sec(x). Its domain is (-∞, -1] U [1, ∞) and its range is [0, π/2) U (π/2, π]. It doesn’t intercept the coordinate axis as it is a discontinuous function. It is neither even nor odd function and is strictly increasing in its domain.](https://anandclasses.in/wp-content/uploads/2025/08/50.png)
Graph of Sec-1(x)
Function Analysis
| Domain | x∈(−∞,−1]∪[1,∞)x∈(−∞,−1]∪[1,∞) |
|---|---|
| Range | y∈[0,π2)∪(π2,π]y∈[0,2π)∪(2π,π] |
| X – Intercept | x=1x=1 |
| Y – Intercept | ϕϕ |
| Minima | (1,0)(1,0) |
| Maxima | (−1,π)(−1,π) |
| Inflection Points | The function does not have any inflection points. |
| Parity | Neither Even Nor Odd |
| Monotonicity | In (1, ∞) it is increasing and in (-∞, -1) it is increasing |
| Asymptotes | y=π2y=2π |
Sample Problems on Inverse of Secant Function
Problem 1: Find the principal value of the given equation:
y = sec-1(√2)
Solution:
We are given that:
y = sec-1(√2)
So we can say that,
sec(y) = (√2)
We know that the range of the principal value branch of sec-1(x) is [0, π] – {π/2} and sec(π/4) = √2.
So, the principal value of sec-1(√2) = π/4.
Problem 2: Find the principal value of the given equation:
y = sec-1(1)
Solution:
We are given that:
y = sec-1(1)
So we can say that,
sec(y) = 1
We know that the range of the principal value branch of sec-1(x) is [0, π] – {π/2} and sec(0) = 1.
So, the principal value of sec-1(1) = 0.
Inverse of Cotangent Function, y = cot-1(x)
cot-1(x) is the inverse function of cot(x). Its domain is ℝ and its range is (0, π). It intersects the coordinate axis at (0, π/2). It is neither even nor odd function and is strictly decreasing in its domain.
Graph of Function
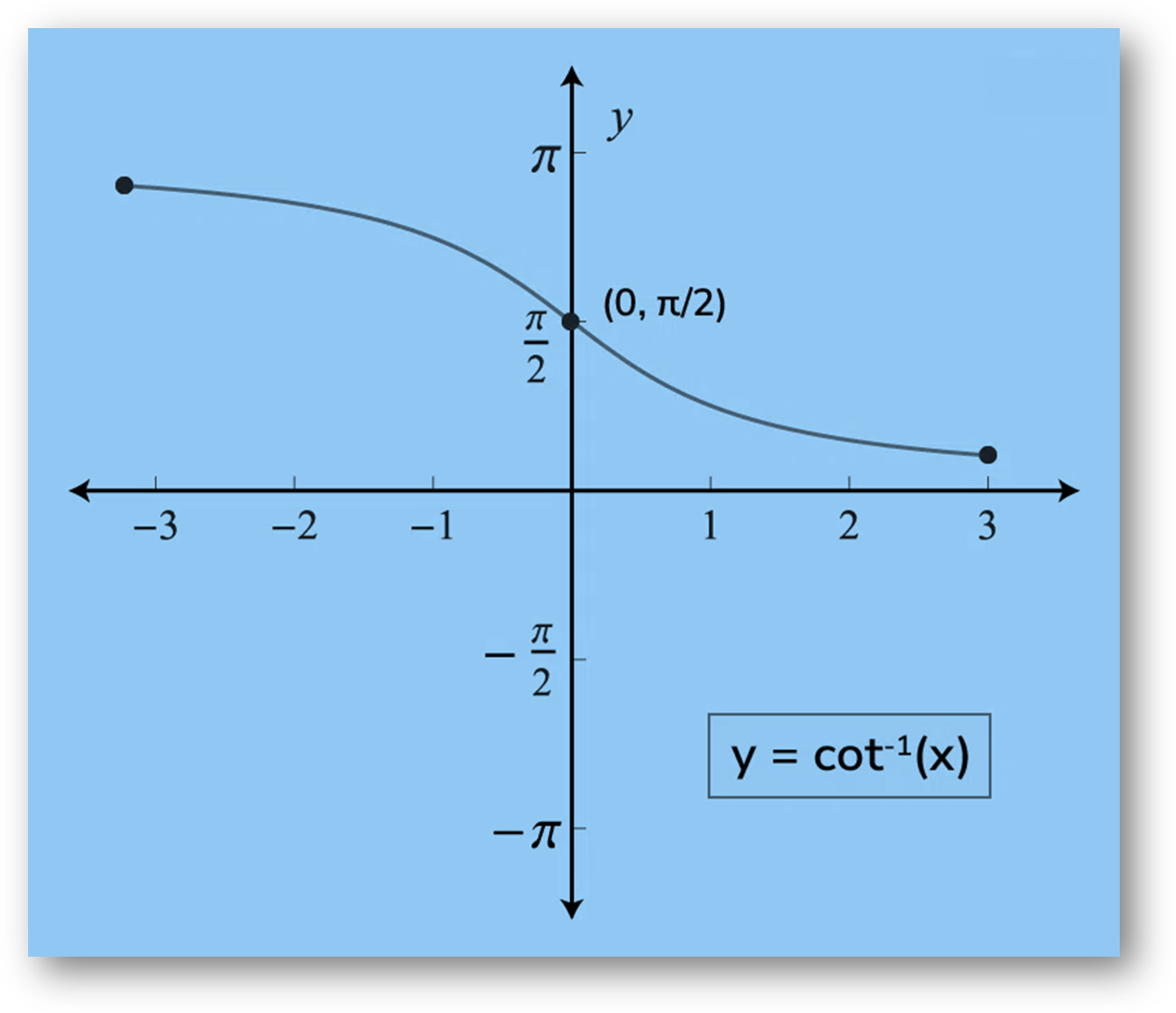
Graph of Cot-1(x)
Function Analysis
| Domain | x∈Rx∈R |
|---|---|
| Range | y∈(0,π)y∈(0,π) |
| X – Intercept | x = null |
| Y – Intercept | y=π2y=2π |
| Minima | The function does not have any minima points. |
| Maxima | The function does not have any maxima points. |
| Inflection Points | The function does not have any inflection points. |
| Parity | Neither Even Nor Odd |
| Monotonicity | In (-∞, ∞) strictly decreasing |
| Asymptotes | y=0 and y=πy=0 and y=π |
Sample Problems on Inverse of Cotangent Function
Problem 1: Find the principal value of the given equation:
y = cot-1(1)
Solution:
We are given that:
y = cot-1(1)
So we can say that,
cot(y) = 1
We know that the range of the principal value branch of cot-1(x) is (-π/2, π/2) and cot(π/4) = 1.
So, the principal value of cot-1(1) = π/4.
Problem 2: Find the principal value of the given equation:
y = cot-1(1/√3)
Solution:
We are given that:
y = cot-1(1/√3)
So we can say that,
cot(y) = (1/√3)
We know that the range of the principal value branch of cot-1(x) is (-π/2, π/2) and cot(π/3) = 1/√3.
So, the principal value of cot-1(1/√3) = π/3.


