Anand Classes provides NCERT Solutions for Class 11 Maths Chapter 10 – Conic Sections (Miscellaneous Exercise) as per the latest NCERT and CBSE syllabus (2025–2026). This exercise includes a comprehensive mix of questions covering all types of conic sections — Circle, Parabola, Ellipse, and Hyperbola. Students can practice application-based problems involving standard equations, latus rectum, eccentricity, foci, directrix, and geometrical properties of different conic curves. Each solution is explained step-by-step to help students master coordinate geometry and prepare efficiently for CBSE Board Exams, JEE Main, JEE Advanced, NDA, and CUET. Click the print button to download study material and notes.
NCERT Question.1 : A parabolic reflector is 20 cm in diameter and 5 cm deep. Find the focus.
Solution :
Take the vertex of the parabolic section as the origin and the axis of the reflector along the positive $x$–axis.
Then the parabola has the standard rightward form
$$y^2 = 4ax.$$
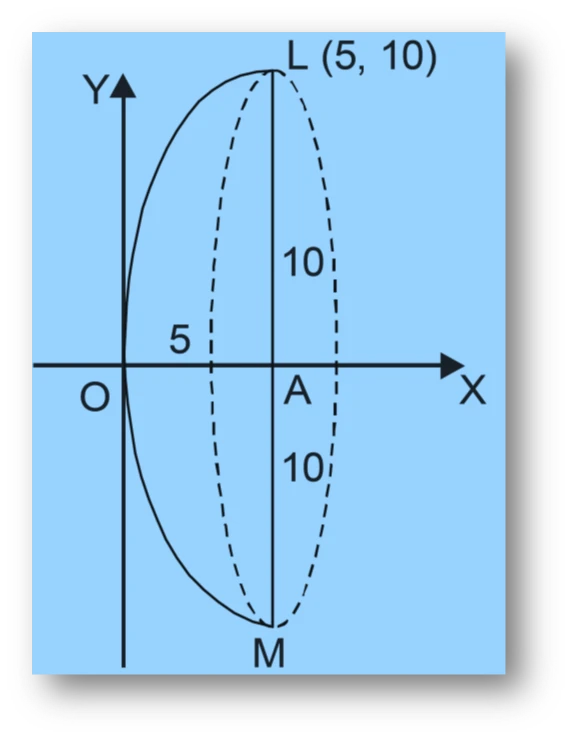
Depth $OA=5\ \text{cm}$ (distance from vertex to rim along the axis) and diameter $LM=20\ \text{cm}$, so half the diameter is $AL=10\ \text{cm}$. Thus a rim point $L$ has coordinates $(5,,10)$.
Point $L$ lies on the parabola, so substitute into $y^2=4ax$:
$$10^2 = 4a(5).$$
Compute $a$ step by step:
$$100 = 20a \quad\Rightarrow\quad a=\frac{100}{20}=5.$$
The focus is at $(a,0)$, so
$$\boxed{(5,,0)}.$$
That is, the focus lies $5\ \text{cm}$ from the vertex along the axis (the midpoint of the rim diameter measured along the axis).
NCERT Question.2 : An arch is in the form of a parabola with its axis vertical. The arch is $10\ \text{m}$ high and $5\ \text{m}$ wide at the base. How wide is it $2\ \text{m}$ from the vertex of the parabola?
Solution :
Take the vertex of the parabola as the origin $O$ and the axis along the positive $y$–axis (upwards).
A downward-opening parabola with vertex at the origin has the form
$$x^2 = -4ay.$$
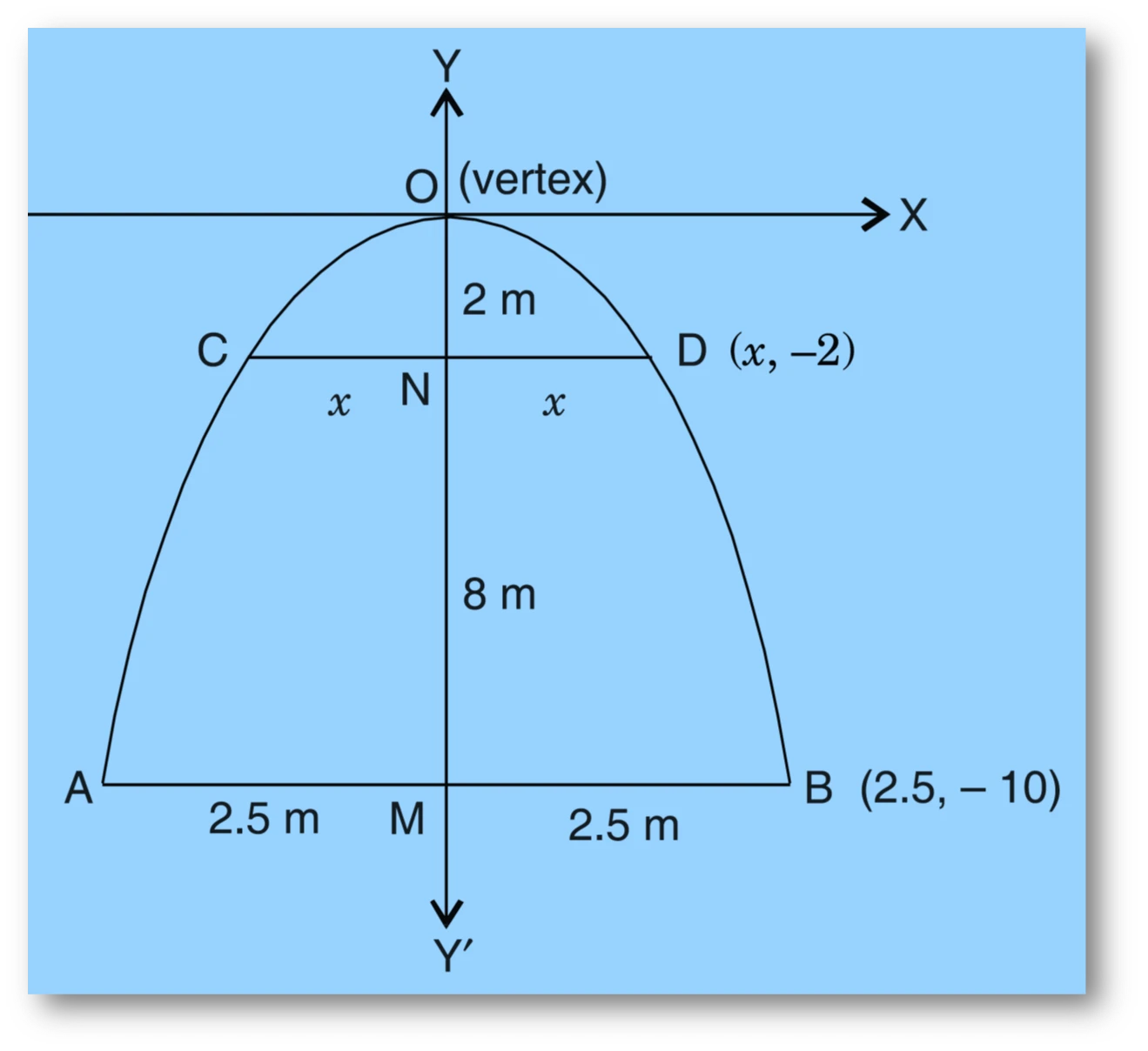
The arch height (depth) from the vertex to the base is $OM=10\ \text{m}$, and half the base is $MB = \dfrac{5}{2}=2.5\ \text{m}$.
Thus one rim point $B$ (on the parabola) has coordinates $(2.5,-10)$.
Substituting $(2.5,-10)$ into $x^2=-4ay$ gives
$$ (2.5)^2 = -4a(-10). $$
Compute $a$:
$$6.25 = 40a \quad\Rightarrow\quad a=\frac{6.25}{40}=\frac{5}{32}.$$
So the parabola equation becomes
$$ x^2 = -4\left(\frac{5}{32}\right)y $$
$$ x^2 = -\frac{5}{8}y $$
$$ x^2 = -0.625y$$
Let the width at a vertical distance $2\ \text{m}$ ($=ON$) from the vertex (i.e. at $y=-2$) be $CD$ and let $CD=2x$ where $D$ has coordinates $(x,-2)$. Substituting into the parabola equation:
$$ x^2 = -0.625(-2) = 1.25 = \frac{5}{4}. $$
Hence
$$ x = \sqrt{\frac{5}{4}}=\frac{\sqrt{5}}{2}. $$
Therefore the width at $2\ \text{m}$ from the vertex is
$$ CD = 2x = 2\cdot\frac{\sqrt{5}}{2}=\sqrt{5}\ \text{m}\approx 2.236\ \text{m}. $$
Answer: The arch is $\sqrt{5}\ \text{m}\approx 2.236\ \text{m}$ wide at $2\ \text{m}$ from the vertex.
Download detailed NCERT solutions by Anand Classes for Class 11 Maths, JEE Main, NDA, and CUET preparation.
NCERT Question.3 : The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The horizontal roadway is 100 m long and is supported by vertical wires attached to the cable. The longest supporting wire is 30 m and the shortest is 6 m. Find the length of the supporting wire attached to the roadway 18 m from the middle.
Solution :
Let the cable of suspension bridge (hanging in the form of a parabola) be the parabolic arc $COB$ with vertex at the lowest point $O$ and axis vertical. Let $LM = 100 m$ be the horizontal roadway such that $CL = BM$ = (longest wire) $30 m$ and $OA$ = (shortest wire) $6 m$. Therefore $O$, the vertex of the parabola is the lowest point of this upward parabola. The parabola is upward-opening with equation
$$x^2 = 4ay.$$
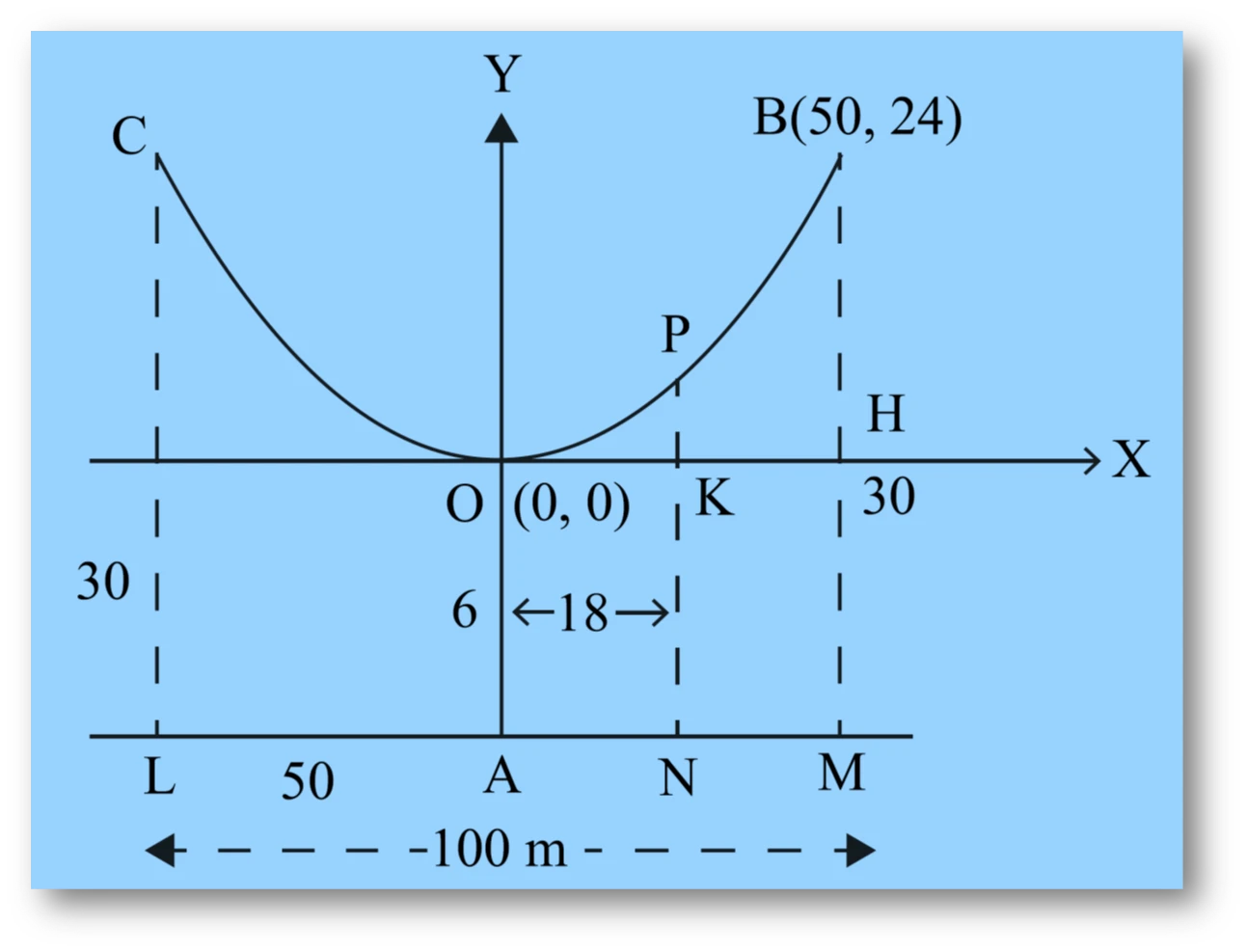
We have to find the length of supporting wire $NP$ attached to the roadway at $N$ where $AN = 18 m$. Now $AL = AM = 50m$. (because $LM = 100m$).
Let the coordinate axes be chosen as shown in the figure. We know that equation of the upward parabola with vertex at $O(0,0)$ and axis along positive y-axis is
$$x^2 = 4ay…………..(i) $$
Since it passes through the point $B$ whose co-ordinates are
$$ x = OH = AM = 50 $$
and
$$ y = BH = BM – HM = BM – OA = 30 – 6 = 24 $$
Putting $x = 50$ and $y = 24 $ in $(i)$ to determine $a$, we have
$$50^2 = 4a(24)\quad\Rightarrow\quad 2500 = 96a\quad\Rightarrow\quad a=\frac{2500}{96}=\frac{625}{24}.$$
Hence
$$4a=\frac{2500}{24}=\frac{625}{6},$$
and the equation of parabola is
$$x^2=\frac{625}{6}y ………(ii) $$
Through the point $N$ draw a vertical line to meet the parabola at point $P$. Then co-ordinates of point $P$ are
$$x = OK = AN = 18 $$
and
$$ y = PK = PN – KN = PN – OA = PN – 6 $$
Putting these values of $x$ and $y$ in $(ii)$
$$(18)^2=\frac{625}{6} (PN-6) $$
Therefore, $$PN = 6 + 3.2704 = 9.2704 $$
∴ Length of the supporting wire attached to the roadway at point $N$ which is 18m from the middle point $A = PN = 9.2704m$.
Answer
The supporting wire attached $18\ \text{m}$ from the middle is approximately $\boxed{9.2704\ \text{m}}$ long.
NCERT Question.4 : An arch is in the form of a semi-ellipse. It is 8 m wide and 2 m high at the centre. Find the height of the arch at a point 1.5 m from one end.
Solution :
Take the centre of the ellipse as the origin $O$ and the horizontal axis along the base.
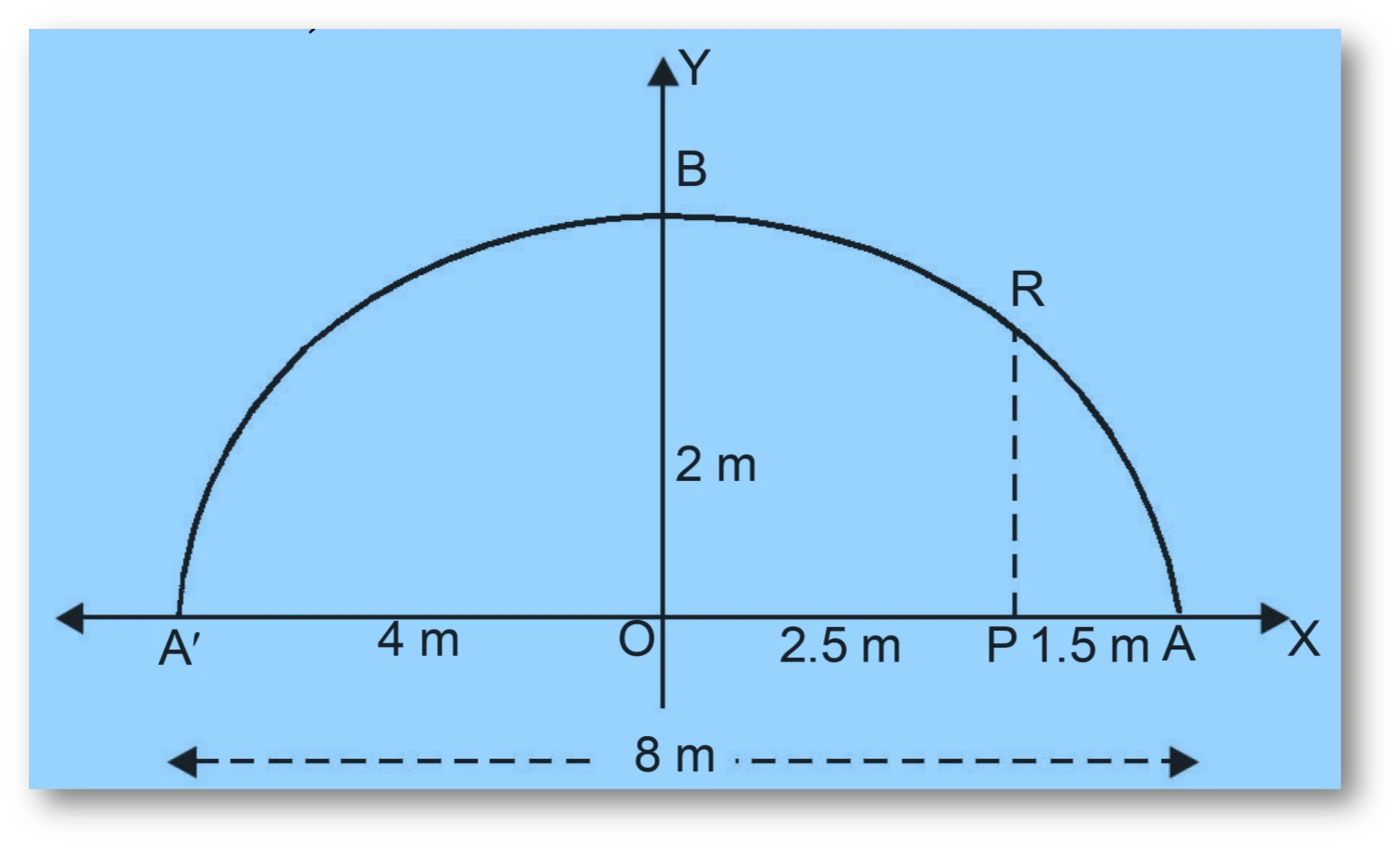
Let $ABA′$ be the given semi-elliptic arch such that width $AA′ = 8 m$ and $OB = 2 m$. The arch is a part of ellipse whose semi-major axis is $\dfrac{8}{2}=4\ \text{m}$ and semi-minor axis is $OB = 2 m$.
i.e., $a = 4 m, b = 2 m$
So the ellipse (upper half) has equation
$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$
or
$$\frac{x^2}{16}+\frac{y^2}{4}=1.$$
We have to find the height $PR$ at $P$ where $AP$ (distance from one end say $A$ of the arch $APA’$) $= 1.5 m$.
Now $OP = OA – AP = 4 – 1.5 = 2.5 m$
Let $A$ be the left end of the base and $P$ be the point on the base with $AP=1.5\ \text{m}$.
The $x$–coordinate of $P$ measured from the centre $O$ is
$$x = OP = OA – AP = 4 – 1.5 = 2.5\ \text{m}.$$
Substitute $x=2.5$ into the ellipse equation:
$$\frac{(2.5)^2}{16}+\frac{y^2}{4}=1.$$
Compute:
$$\frac{6.25}{16}+\frac{y^2}{4}=1 \quad\Rightarrow\quad \frac{y^2}{4}=1-\frac{6.25}{16}=0.609375.$$
Thus
$$y^2 = 4\times 0.609375 = 2.4375$$
and
$$y=\sqrt{2.4375}\approx 1.5617\ \text{m}.$$
Answer
The height of the arch at the point 1.5 m from one end is approximately $\boxed{1.56\ \text{m}}$.


