Anand Classes provides comprehensive NCERT Solutions for the Miscellaneous Exercise of Chapter 8 Applications of Integrals for Class 12 Mathematics, helping students master the concepts of area under curves, geometrical interpretation, and problem-solving through clear, step-by-step explanations. These notes strictly follow the latest NCERT syllabus and are perfect for board exam preparation, revision, and strengthening conceptual understanding. Click the print button to download study material and notes.
NCERT Question.1 (i) : Find area under the given curve $\;y = x^{2}\;$ and given lines $\; x = 1, x = 2\;$ and the x-axis.
Solution :

Required area is:
$$
A=\int_{1}^{2} x^{2}\;dx
$$
Integrate:
$$
A=\left[\frac{x^{3}}{3}\right]_{1}^{2}
$$
Substitute the limits:
$$
A=\frac{2^{3}}{3}-\frac{1^{3}}{3}
= \frac{8}{3}-\frac{1}{3}
= \frac{7}{3}
$$
Final Answer
$$ \boxed{\frac{7}{3}} $$
NCERT Question.1(ii) : Find the area under the given curve $ y = x^{4}$ and the lines $ x = 1, x = 5 $, and the x-axis.
Solution
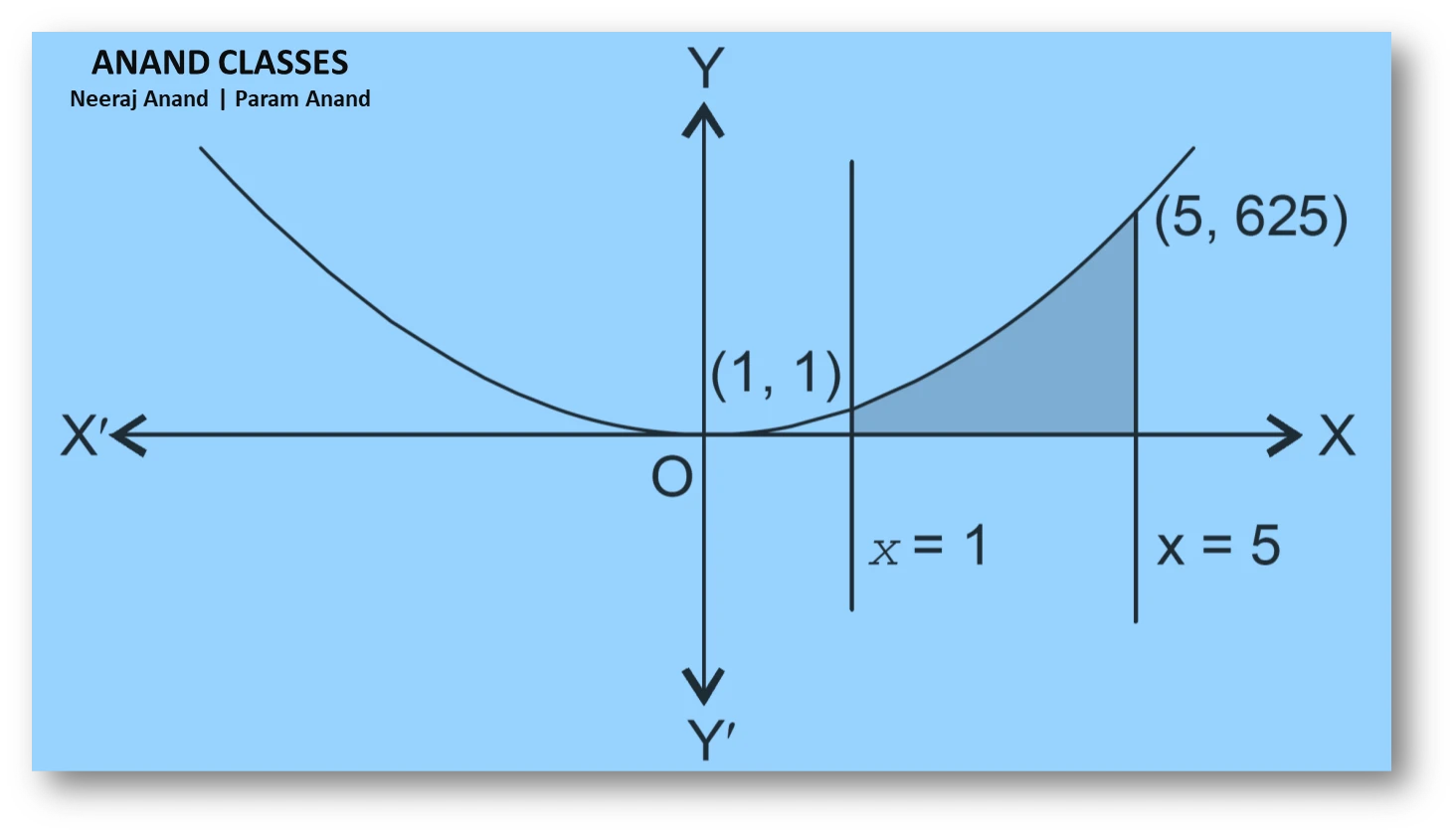
Required area:
$$
A = \int_{1}^{5} x^{4}\;dx
$$
Integrate:
$$
A = \left[ \frac{x^{5}}{5} \right]_{1}^{5}
$$
Substitute limits:
$$
A = \frac{5^{5}}{5} – \frac{1^{5}}{5}
$$
$$
A = \frac{3125}{5} – \frac{1}{5}
= \frac{3124}{5} = 624.8
$$
Final Answer
$$
\boxed{\frac{3124}{5}}=624.8
$$
Unlock more expertly crafted solutions and downloadable notes with Anand Classes, ideal for CBSE and JEE preparation. Get step-wise mathematics explanations, area-under-curve problems, and complete chapter notes for stronger exam performance.
NCERT Question.2 : Sketch the graph of $y=|x+3|$ and evaluate $\displaystyle \int_{-6}^{0}|x+3|\;dx$
Solution
The function $y=|x+3|$ is piecewise:
$$
y=|x+3|=\begin{cases}
-(x+3), & x\le -3,\\
x+3, & x\ge -3.
\end{cases}
$$
Corresponding values of $x$ and $y$ are given in the following table.
| $x$ | $y$ |
|---|---|
| -6 | 3 |
| -5 | 2 |
| -4 | 1 |
| -3 | 0 |
| -2 | 1 |
| -1 | 2 |
| 0 | 3 |
The graph is a V-shaped curve with vertex at $(-3,0)$. On the interval $[-6,-3]$ it is the line $y=-(x+3)$ (sloping up to the right), and on $[-3,0]$ it is the line $y=x+3$.
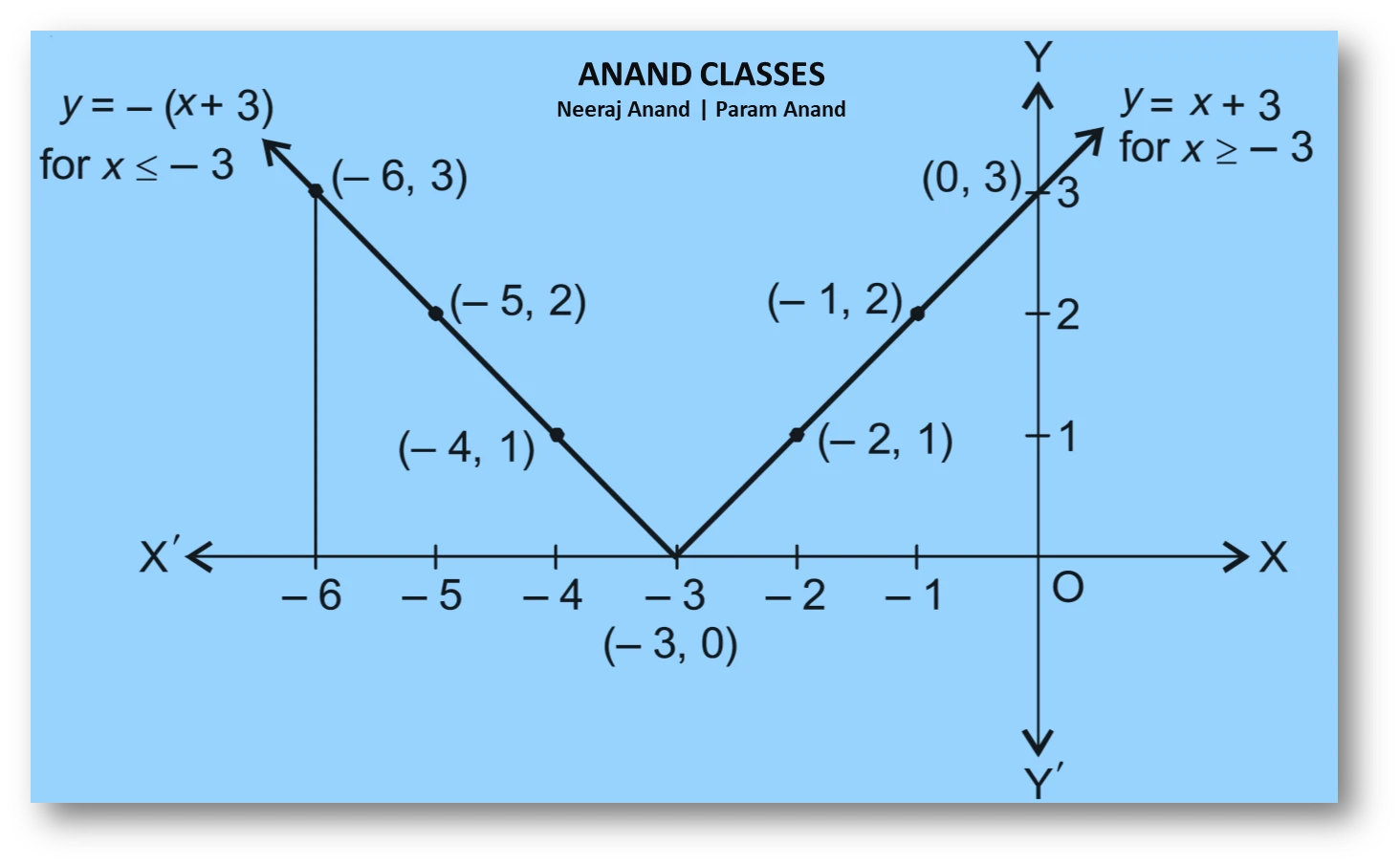
To evaluate the integral, split at the corner $(x=-3)$ :
$$
\int_{-6}^{0}|x+3|\;dx
=\int_{-6}^{-3}-(x+3)\;dx+\int_{-3}^{0}(x+3)\;dx.
$$
Compute each part.
- For the left piece:
$$
\int_{-6}^{-3}-(x+3)\;dx
=-\Big[\frac{x^{2}}{2}+3x\Big]_{-6}^{-3}=\\[1em]
=-\big(\big(\frac{9}{2}-9\big)-\big(18-18\big)\big)
=-\big(-\frac{9}{2}-0\big)=\frac{9}{2}.
$$ - For the right piece:
$$
\int_{-3}^{0}(x+3)\;dx
=\Big[\frac{x^{2}}{2}+3x\Big]_{-3}^{0}
=0-\big(\frac{9}{2}-9\big)=\frac{9}{2}.
$$
Add them:
$$
\int_{-6}^{0}|x+3|,dx=\frac{9}{2}+\frac{9}{2}=9.
$$
Final Answer
$$\boxed{\;\displaystyle \int_{-6}^{0}|x+3|\;dx = 9\;}$$
Unlock more worked problems and downloadable notes from Anand Classes — clear step-by-step solutions for absolute-value graphs, definite integrals, and exam-focused practice perfect for CBSE and JEE preparation.
NCERT Question.3 : Find the area bounded by the curve $y=\sin x$ between $x=0$ and $x=2\pi$.
Solution
The area between the curve and the $x$-axis is the integral of $|\sin x|$ from $0$ to $2\pi$. Split at the zero of $\sin x$ at $x=\pi$ :
$$
\text{Area}=\int_{0}^{2\pi}|\sin x|\;dx
=\left|\int_{0}^{\pi}\sin x\;dx\right|+\left|\int_{\pi}^{2\pi}\sin x\;dx\right|
$$

Compute each integral:
$$
\int_{0}^{\pi}\sin x\;dx=\big[-\cos x\big]_{0}^{\pi}=(-\cos\pi)-(-\cos0)=(-(-1))-(-1)=2,
$$
$$
\int_{\pi}^{2\pi}\sin x\;dx=\big[-\cos x\big]{\pi}^{2\pi}=(-\cos 2\pi)-(-\cos\pi)=(-1)-1=-2,
$$
so, $$\left|\int_{\pi}^{2\pi}\sin x\;dx\right|=2$$
Therefore
$$
\text{Area}=\int_{0}^{2\pi}|\sin x|\;dx =| 2 |+|- 2 |
$$
$$
\text{Area}=2+2=4.
$$
Final Answer
$$
\boxed{\;4\;\text{square units}\;}
$$
Download more worked solutions and complete chapter notes from Anand Classes—perfect for JEE and CBSE revision, clear step-by-step integrations, and reliable exam practice.
NCERT Question.4 : Choose the correct answer:
Area bounded by the curve $y = x^{3}$, the $x$–axis and the ordinates $x=-2$ and $x=1$ is:
(A) $-9$
(B) $-\frac{15}{4}$
(C) $\frac{15}{4}$
(D) $\frac{17}{4}$
Solution :
To find the area bounded by the curve $y = x^{3}$ the $x$–axis and the ordinates $x=-2$ and $x=1$, we integrate $ x^3 $ with respect to $x$ over the interval [−2, 1].

$$
\text{Area}=\int_{-2}^{0}\big|x^{3}\big|\;dx+\int_{0}^{1}\big|x^{3}\big|\;dx.
$$
On [-2, 0] we have $x^{3}\le0$, so $|x^{3}|=-x^{3}$. On [0, 1] we have $|x^{3}|=x^{3}$. Thus
$$
\int_{-2}^{0}\big|x^{3}\big|\;dx =\int_{-2}^{0}(-x^{3})\;dx $$
$$\int_{-2}^{0}\big|x^{3}\big|\;dx=-\left[\frac{x^{4}}{4}\right]_{-2}^{0}=-\bigg(0-\frac{(-2)^{4}}{4}\bigg)=-\bigg(0-\frac{16}{4}\bigg)=4$$
$$\int_{0}^{1}\big|x^{3}\big|\;dx =\int_{0}^{1}x^{3}\;dx
=\left[\frac{x^{4}}{4}\right]_{0}^{1}=\frac{1}{4}$$
So the total area is
$$
\text{Area}=4+\frac{1}{4}=\frac{17}{4}.
$$
Correct option: (D) $(\dfrac{17}{4}).$
Explore more solved MCQs, integrals, and area-under-curve problems with step-by-step explanations from Anand Classes—ideal for strengthening concepts for JEE and CBSE exams.
NCERT Question.5 : Choose the correct answer:
The area bounded by the curve $y = x | x |$ , $x$-axis and the ordinates $x = – 1$ and $x = 1$ is given by
(A) 0
(B) 1/ 3
(C) 2/3
(D) 4/3
Solution
The curve is
$$ y = x|x|. $$
This splits into two cases:
- For $x \ge 0$:
$$ |x| = x\Rightarrow y = x^{2} $$ - For $x < 0$:
$$ |x| = -x \Rightarrow y = -x^{2} $$
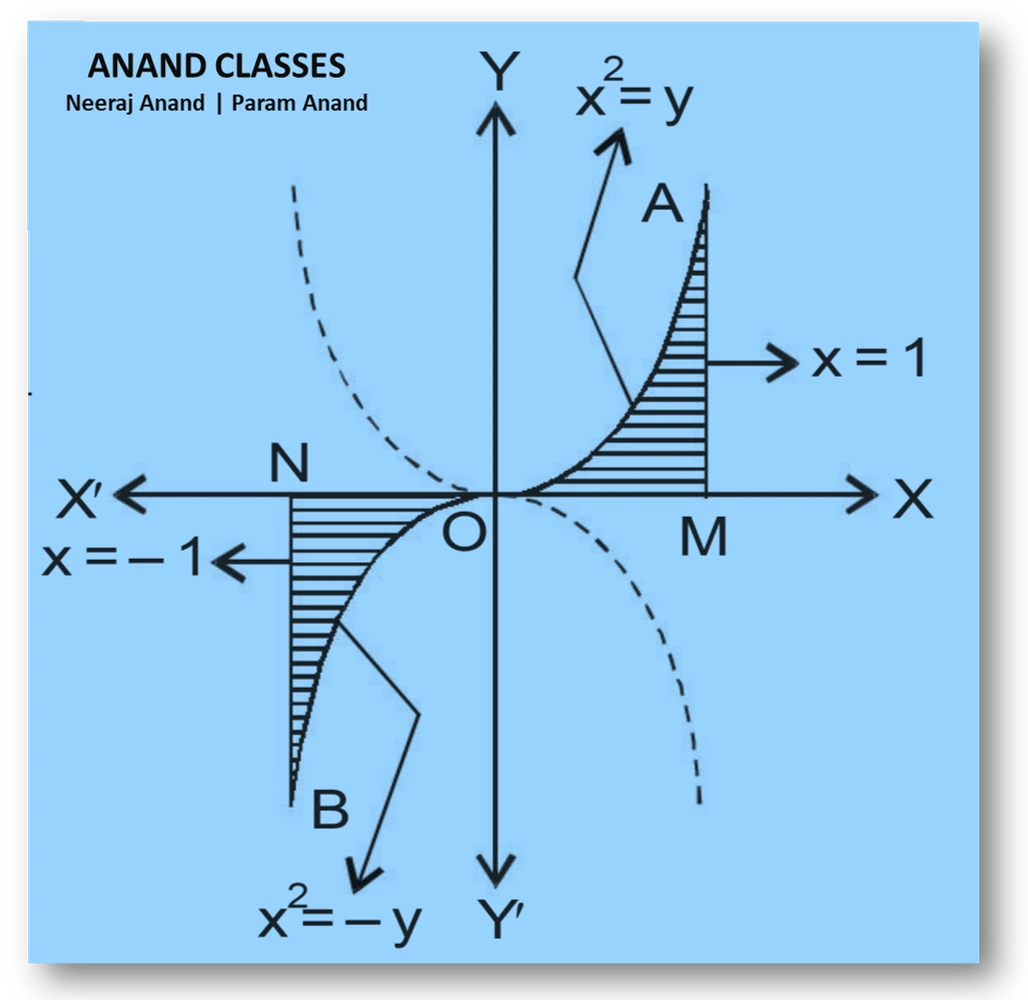
We find area separately on each interval.
For $0 \le x \le 1$:
$$
\text{Area}_{1} = \int_{0}^{1} x^{2}\;dx
= \left( \frac{x^{3}}{3} \right)_{0}^{1}
= \frac{1}{3}.
$$
For $-1 \le x < 0$:
$$
\text{Area}_{2} = \int_{-1}^{0} -x^{2}\;dx
= \left( -\frac{x^{3}}{3} \right)_{-1}^{0}
= \frac{1}{3}.
$$
Total Area
$$
\text{Total Area} = \frac{1}{3} + \frac{1}{3}
= \frac{2}{3}.
$$
✔ Correct option: (C) $\dfrac{2}{3}$
Get more clean, exam-focused calculus solutions, perfectly formatted for CBSE and JEE preparation, with premium-quality notes from Anand Classes—ideal for strengthening your understanding of applications of integrals.
Summary
Chapter 8 of the Class 12 NCERT Mathematics Part II textbook, “Application of Integrals,” focuses on the practical uses of integration. The Miscellaneous Exercise covers various problems where integrals are used to compute areas under curves, volumes of solids of revolution, and other applications. The exercise helps students practice and apply integration techniques to solve real-world problems involving geometric shapes and physical quantities.


