Conic Sections (Circles) NCERT Solutions Exercise 10.1 Class 11 Math (Set-2)

Anand Classes offers NCERT Solutions for Class 11 Maths Chapter 10 – Conic Sections (Exercise 10.1) based on the latest NCERT and CBSE curriculum (2025–2026). This exercise helps students understand the basic concepts of conic sections, including the circle, ellipse, parabola, and hyperbola, with detailed derivations, standard equations, and geometrical interpretation. Each question is solved step-by-step to make learning easier and build strong fundamentals in coordinate geometry. These solutions are perfect for CBSE board preparation as well as for entrance exams like JEE Main, JEE Advanced, NDA, and CUET. Click the print button to download study material and notes.

---

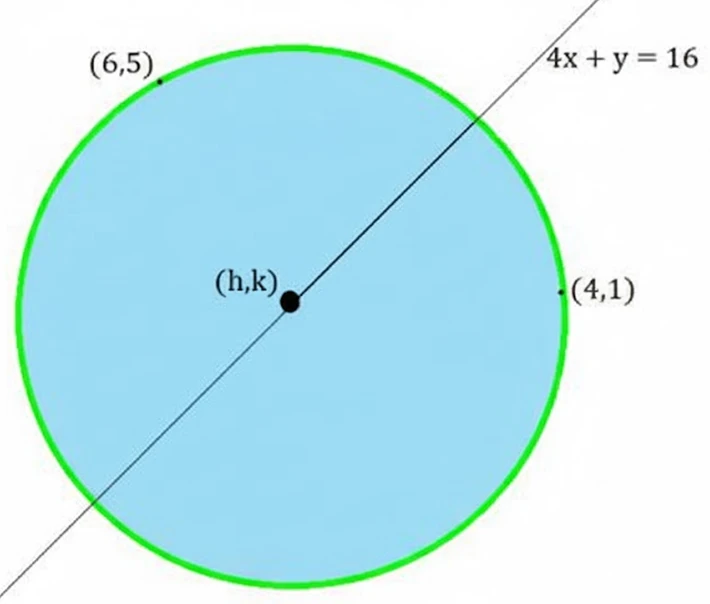
NCERT Question.10 : Find the equation of the circle passing through the points (4, 1) and (6, 5) and whose centre is on the line 4x + y = 16.

Solution :
The equation of the circle is $(x – h)^2 + (y – k)^2 = r^2$.

As the circle passes through points $(4, 1)$ and $(6, 5)$,

For point $(4, 1)$:
$(4 – h)^2 + (1 – k)^2 = r^2 \ \text{……(1)}$

For point $(6, 5)$:
$(6 – h)^2 + (5 – k)^2 = r^2 \ \text{……(2)}$

Given that the centre $(h, k)$ lies on the line $4x + y = 16$,
so $4h + k = 16 \ \text{……(3)}$

From equations (1) and (2):
$(4 – h)^2 + (1 – k)^2 = (6 – h)^2 + (5 – k)^2$

Expanding,
$16 – 8h + h^2 + 1 – 2k + k^2 = 36 – 12h + h^2 + 25 – 10k + k^2$

Simplifying,
$16 – 8h + 1 – 2k = 36 – 12h + 25 – 10k$

$4h + 8k = 44$

$h + 2k = 11 \ \text{……(4)}$

Now, multiply equation (3) by 2 and subtract it from equation (4):

$(h + 2k) – 2(4h + k) = 11 – 32$

$h + 2k – 8h – 2k = -21$

$-7h = -21$

$\therefore h = 3$

Substitute $h = 3$ in equation (4):

$3 + 2k = 11$

$2k = 8 \Rightarrow k = 4$

Thus, $h = 3$ and $k = 4$.

Now substitute these in equation (1):

$(4 – 3)^2 + (1 – 4)^2 = r^2$

$1^2 + (-3)^2 = r^2$

$1 + 9 = r^2$

$\therefore r = \sqrt{10}$

Hence, the equation of the circle is
$(x – 3)^2 + (y – 4)^2 = (\sqrt{10})^2$

Expanding,
$x^2 – 6x + 9 + y^2 – 8y + 16 = 10$

$x^2 + y^2 – 6x – 8y + 15 = 0$

Therefore, the equation of the circle is $x^2 + y^2 – 6x – 8y + 15 = 0$.

---

NCERT Question.11 : Find the equation of the circle passing through the points (2, 3) and (–1, 1) and whose centre is on the line x – 3y – 11 = 0.

Solution :
The equation of the circle is $(x – h)^2 + (y – k)^2 = r^2$.

As the circle passes through points $(2, 3)$ and $(-1, 1)$,

For point $(2, 3)$:
$(2 – h)^2 + (3 – k)^2 = r^2 \ \text{……(1)}$

For point $(-1, 1)$:
$(-1 – h)^2 + (1 – k)^2 = r^2 \ \text{……(2)}$

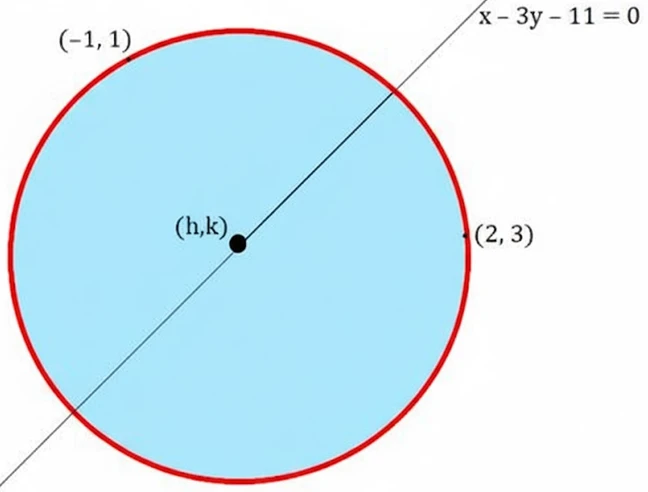
Given that the centre $(h, k)$ lies on the line $x – 3y – 11 = 0$,
so $h – 3k = 11 \ \text{……(3)}$

From equations (1) and (2):
$(2 – h)^2 + (3 – k)^2 = (-1 – h)^2 + (1 – k)^2$

Expanding,
$4 – 4h + h^2 + 9 – 6k + k^2 = 1 + 2h + h^2 + 1 – 2k + k^2$

Simplifying,
$4 – 4h + 9 – 6k = 2 + 2h – 2k$

$6h + 4k = 11 \ \text{……(4)}$

Now multiply equation (3) by 6 and subtract it from equation (4):

$6h + 4k – 6(h – 3k) = 11 – 66$

$6h + 4k – 6h + 18k = -55$

$22k = -55 \Rightarrow k = -\dfrac{5}{2}$

Substitute $k = -\dfrac{5}{2}$ in equation (4):

$6h + 4(-\dfrac{5}{2}) = 11$

$6h – 10 = 11$

$6h = 21 \Rightarrow h = \dfrac{7}{2}$

Thus, $h = \dfrac{7}{2}$ and $k = -\dfrac{5}{2}$.

Substitute these values in equation (1):

$(2 – \dfrac{7}{2})^2 + (3 + \dfrac{5}{2})^2 = r^2$

$\left(\dfrac{-3}{2}\right)^2 + \left(\dfrac{11}{2}\right)^2 = r^2$

$\dfrac{9}{4} + \dfrac{121}{4} = r^2$

$\dfrac{130}{4} = r^2$

Hence, the equation of the circle is
$(x – \dfrac{7}{2})^2 + (y + \dfrac{5}{2})^2 = \dfrac{130}{4}$

Expanding,
$x^2 + y^2 – 7x + 5y – 14 = 0$

Therefore, the equation of the circle is $x^2 + y^2 – 7x + 5y – 14 = 0$.

Download detailed NCERT solutions by Anand Classes for Class 11 Maths, JEE Main, NDA, and CUET Exams.

---

NCERT Question 12 : Find the equation of the circle with radius 5 whose centre lies on x-axis and passes through the point (2, 3).

Solution:
The equation of a circle is given by
$$(x – h)^2 + (y – k)^2 = r^2$$

Given that the radius $r = 5$ and the centre lies on the x-axis, so $k = 0$.
Hence, the equation of the circle becomes:
$$(x – h)^2 + y^2 = 25$$

Since the circle passes through the point $(2, 3)$,
$$(2 – h)^2 + 3^2 = 25$$

$$(2 – h)^2 = 25 – 9$$

$$(2 – h)^2 = 16$$

Thus,
$$2 – h = \pm 4$$

If $2 – h = 4$, then $h = -2$
If $2 – h = -4$, then $h = 6$

Case 1: When $h = -2$
$$(x + 2)^2 + y^2 = 25$$

$$x^2 + 4x + 4 + y^2 = 25$$

$$x^2 + y^2 + 4x – 21 = 0$$

Case 2: When $h = 6$
$$(x – 6)^2 + y^2 = 25$$

$$x^2 – 12x + 36 + y^2 = 25$$

$$x^2 + y^2 – 12x + 11 = 0$$

Therefore, the equations of the circles are:
$$x^2 + y^2 + 4x – 21 = 0 \quad \text{and} \quad x^2 + y^2 – 12x + 11 = 0$$

---

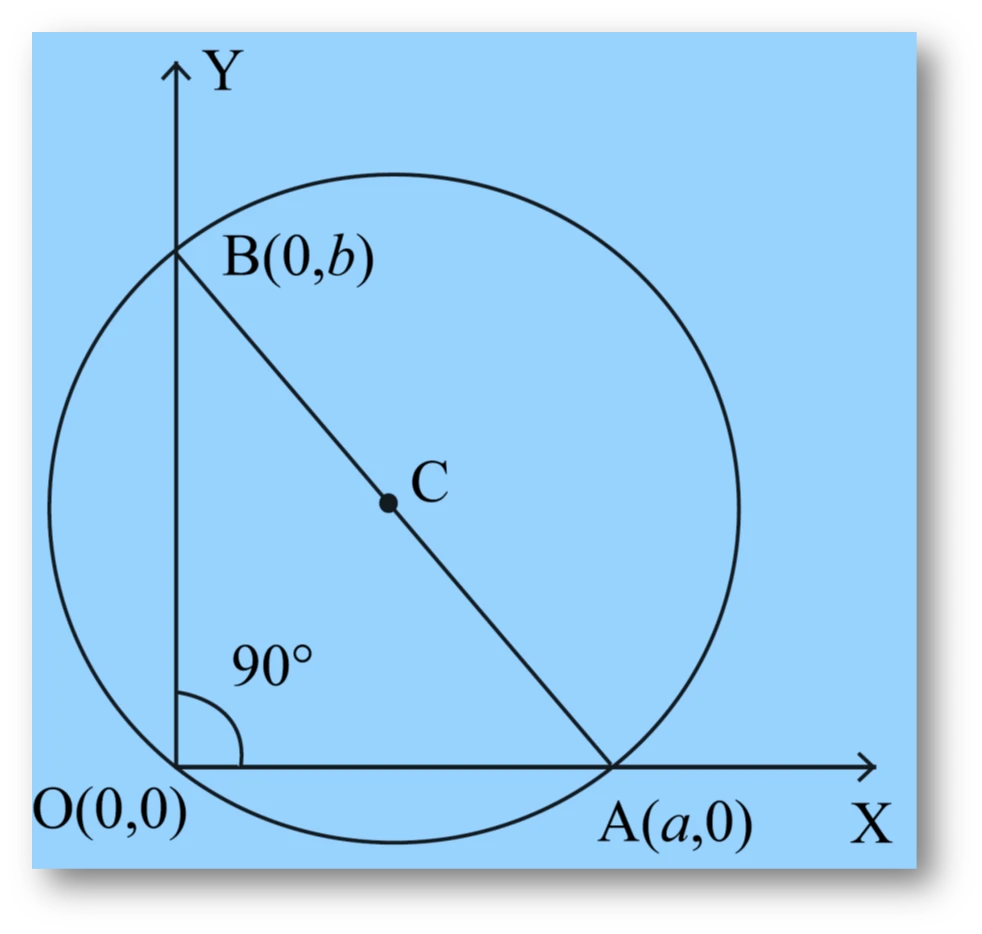
NCERT Question 13 : Find the equation of the circle passing through (0, 0) and making intercepts $a$ and $b$ on the coordinate axes.

Solution:
The general equation of a circle is
$$(x – h)^2 + (y – k)^2 = r^2$$

Since the circle passes through $(0, 0)$,
$$(-h)^2 + (-k)^2 = r^2$$

$$h^2 + k^2 = r^2$$

Hence,
$$(x – h)^2 + (y – k)^2 = h^2 + k^2$$

The circle cuts intercepts $a$ and $b$ on the coordinate axes, i.e., it passes through $(a, 0)$ and $(0, b)$.

Substituting $(a, 0)$ in the equation:
$$(a – h)^2 + (0 – k)^2 = h^2 + k^2$$

$$a^2 – 2ah + h^2 + k^2 = h^2 + k^2$$

$$a^2 – 2ah = 0$$

$$a(a – 2h) = 0$$

Since $a \ne 0$, we get
$$h = \frac{a}{2}$$

Substituting $(0, b)$ in the equation:
$$(-h)^2 + (b – k)^2 = h^2 + k^2$$

$$h^2 + b^2 – 2bk + k^2 = h^2 + k^2$$

$$b^2 – 2bk = 0$$

$$b(b – 2k) = 0$$

Since $b \ne 0$, we get
$$k = \frac{b}{2}$$

Now substituting $h = \frac{a}{2}$ and $k = \frac{b}{2}$, we get
$$(x – \frac{a}{2})^2 + (y – \frac{b}{2})^2 = (\frac{a}{2})^2 + (\frac{b}{2})^2$$

Simplifying,
$$4x^2 – 4ax + a^2 + 4y^2 – 4by + b^2 = a^2 + b^2$$
$$4x^2 + 4y^2 – 4ax – 4by = 0$$

Dividing throughout by 4,
$$x^2 + y^2 – ax – by = 0$$

Therefore, the equation of the circle is:
$$x^2 + y^2 – ax – by = 0$$

For more circle equation examples and geometry problem solutions for Class 11 Maths, JEE Main, and CUET exams, visit Anand Classes‘ comprehensive notes section.

---

NCERT Question 14: Find the equation of a circle with centre (2, 2) and passes through the point (4, 5)

Solution:
Given the centre of the circle as (h, k) = (2, 2).

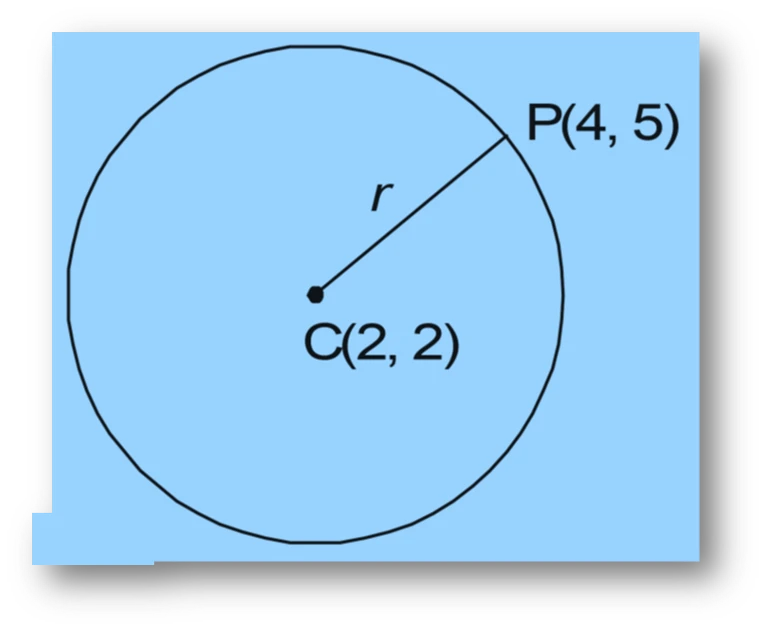
Also, the circle passes through the point (4, 5).
Hence, the radius ( r ) is the distance between the points C(2, 2) and P(4, 5):

r = √[(2 – 4)² + (2 – 5)²]
= √[(-2)² + (-3)²]
= √(4 + 9)
= √13

Now, the equation of the circle is
(x – h)² + (y – k)² = r²

Substituting h = 2, k = 2, and r = √13:

(x – 2)² + (y – 2)² = (√13)²

x² – 4x + 4 + y² – 4y + 4 = 13

x² + y² – 4x – 4y – 5 = 0

Therefore, the equation of the circle is:
x² + y² – 4x – 4y – 5 = 0

---

NCERT Question 15: Does the point (–2.5, 3.5) lie inside, outside or on the circle x² + y² = 25?

Solution:
Given equation of the circle:
x² + y² = 25

This can be written as (x – 0)² + (y – 0)² = 5²
So, the circle has centre (0, 0) and radius r = 5.

Now, the distance between the point (–2.5, 3.5) and the centre (0, 0) is:

√[(-2.5 – 0)² + (3.5 – 0)²]
= √(6.25 + 12.25)
= √18.5
≈ 4.3

Since 4.3 < 5, the distance from the centre is less than the radius.

Therefore, the point (–2.5, 3.5) lies inside the circle.

📘 For more detailed coordinate geometry notes and NCERT solutions on Circles, Straight Lines, and Conic Sections, visit Anand Classes — your trusted resource for Class 11–12 Maths, JEE Main, NDA, and CUET preparation.