Anand Classes provides NCERT Solutions for Class 11 Maths Chapter 9 – Straight Lines (Miscellaneous Exercise) for the 2025–2026 academic year, prepared as per the latest NCERT and CBSE syllabus. This exercise includes a variety of advanced problems based on different forms of straight-line equations, distance formula, angle between lines, concurrent lines, and area of triangles formed by lines. The solutions are presented step-by-step with proper reasoning and geometric interpretation, helping students strengthen their understanding of coordinate geometry and analytical problem-solving. These solutions are invaluable for students preparing for CBSE Board Exams, JEE Main, JEE Advanced, NDA, and CUET. Click the print button to download study material and notes in PDF format.
NCERT Question 1.
Find the values of $k$ for which the line $(k – 3)x – (4 – k^2)y + k^2 – 7k + 6 = 0$ is
(a) Parallel to the x-axis
(b) Parallel to the y-axis
(c) Passing through the origin
Solution:
We are given the line,
$$(k – 3)x – (4 – k^2)y + k^2 – 7k + 6 = 0$$
Rewriting,
$$(4 – k^2)y = (k – 3)x + k^2 – 7k + 6$$
$$\Rightarrow y = \frac{(k – 3)x}{4 – k^2} + \frac{k^2 – 7k + 6}{4 – k^2}$$
The equation of the line is of the form $y = mx + c$, where
$$m = \frac{k – 3}{4 – k^2} \quad \text{and} \quad c = \frac{k^2 – 7k + 6}{4 – k^2}$$
(a) Line parallel to the x-axis
If the line is parallel to the x-axis, then
$$m = 0$$
$$\Rightarrow \frac{k – 3}{4 – k^2} = 0$$
$$\Rightarrow k – 3 = 0$$
$$\Rightarrow k = 3$$
✅ Therefore, for the line to be parallel to the x-axis, $k = 3$.
(b) Line parallel to the y-axis
If the line is parallel to the y-axis, then its slope is undefined:
$$m = \infty$$
This happens when the denominator of $\dfrac{k – 3}{4 – k^2}$ is zero:
$$4 – k^2 = 0$$
$$\Rightarrow k^2 = 4$$
$$\Rightarrow k = \pm 2$$
✅ Therefore, for the line to be parallel to the y-axis, $k = 2$ or $k = -2$.
(c) Line passing through the origin
If the line passes through the origin, then the y-intercept $c = 0$:
$$c = \frac{k^2 – 7k + 6}{4 – k^2} = 0$$
$$\Rightarrow k^2 – 7k + 6 = 0$$
$$\Rightarrow (k – 6)(k – 1) = 0$$
$$\Rightarrow k = 1 \text{ or } k = 6$$
✅ Therefore, for the line to pass through the origin, $k = 1$ or $k = 6$.
This geometry solution is provided by Anand Classes, experts in Class 11–12 coordinate geometry, CBSE, and JEE preparation.
NCERT Question 2 : Find the equations of the lines, which cut-off intercepts on the axes whose sum and product are 1 and –6, respectively.
Solution :
Let the intercepts on the axes be $a$ and $b$. Given
$$a+b=1,\qquad ab=-6.$$
Solve the quadratic whose roots are $a,b$:
$$t^2-(a+b)t+ab=0 \implies t^2-t-6=0.$$
Factor:
$$(t-3)(t+2)=0.$$
Thus $(a,b)=(3,-2)$ or $(a,b)=(-2,3)$.
Equation of a line with intercepts $a,b$ is
$$\frac{x}{a}+\frac{y}{b}=1$$
or equivalently $bx+ay-ab=0$.
For $(a,b)=(3,-2)$:
$$-2x+3y-(-2\cdot3)= -2x+3y+6=0 \iff 2x-3y=6.$$
For $(a,b)=(-2,3)$:
$$3x-2y-(-2\cdot3)=3x-2y+6=0 $$
$$\iff -3x+2y=-6 \iff 3x-2y=-6.$$
So the two lines are
$$2x-3y=6\quad\text{and}\quad 3x-2y=-6.$$
NCERT Question 3 : Find points on the $y$–axis at distance $4$ from the line $\dfrac{x}{3}+\dfrac{y}{4}=1$.
Solution :
Write the line as
$$\frac{x}{3}+\frac{y}{4}=1 \iff 4x+3y-12=0.$$
For a point $(0,b)$ the perpendicular distance to $Ax+By+C=0$ is
$$d=\frac{|A\cdot0+B\cdot b+C|}{\sqrt{A^2+B^2}}=\frac{|3b-12|}{\sqrt{4^2+3^2}}=\frac{|3b-12|}{5}.$$
Set $d=4$:
$$\frac{|3b-12|}{5}=4 \implies |3b-12|=20.$$
So
$$3b-12=20\implies b=\frac{32}{3},\qquad 3b-12=-20\implies b=-\frac{8}{3}.$$
Points on the $y$–axis are
$$\left(0,\frac{32}{3}\right)\quad\text{and}\quad\left(0,-\frac{8}{3}\right).$$
NCERT Question 4. Find the perpendicular distance from the origin to the line joining the points $(\cos \theta, \sin \theta)$ and $(\cos \phi, \sin \phi)$.
Solution:
The equation of the line joining the points $(\cos \theta, \sin \theta)$ and $(\cos \phi, \sin \phi)$ is given by
$$
y – \sin \theta = \frac{\sin \phi – \sin \theta}{\cos \phi – \cos \theta} (x – \cos \theta)
$$
Simplifying,
$$
y(\cos \phi – \cos \theta) – \sin \theta (\cos \phi – \cos \theta) = x(\sin \phi – \sin \theta) – \cos \theta (\sin \phi – \sin \theta)
$$
$
x(\sin \phi – \sin \theta) + y(\cos \phi – \cos \theta) + \cos \theta \sin \phi – \sin \theta \cos \phi – \sin \theta \cos \phi + \sin \theta \cos \theta = 0
$
Simplify further,
$$
x(\sin \phi – \sin \theta) + y(\cos \phi – \cos \theta) + \sin(\phi – \theta) = 0
$$
So,
$A = \sin \phi – \sin \theta$,
$B = \cos \phi – \cos \theta$, and
$C = \sin(\phi – \theta)$.
Now, the perpendicular distance $(d)$ of a line $Ax + By + C = 0$ from the origin $(0, 0)$ is given by
$$
d = \frac{|C|}{\sqrt{A^2 + B^2}}
$$
Substituting the values,
$$
d = \frac{|\sin(\phi – \theta)|}{\sqrt{(\sin \phi – \sin \theta)^2 + (\cos \phi – \cos \theta)^2}}
$$
Simplify the denominator:
$$
d = \frac{|\sin(\phi – \theta)|}{\sqrt{\sin^2 \phi + \sin^2 \theta – 2 \sin \phi \sin \theta + \cos^2 \phi + \cos^2 \theta – 2 \cos \phi \cos \theta}}
$$
$$
d = \frac{|\sin(\phi – \theta)|}{\sqrt{2 – 2(\sin \phi \sin \theta + \cos \phi \cos \theta)}}
$$
Using the trigonometric identity $cos(phi – theta) = cos phi cos theta + sin phi sin theta$, we get
$$
d = \frac{|\sin(\phi – \theta)|}{\sqrt{2(1 – \cos(\phi – \theta))}}
$$
Now,
$$
1 – \cos(\phi – \theta) = 2\sin^2\left(\frac{\phi – \theta}{2}\right)
$$
Hence,
$$
d = \frac{|\sin(\phi – \theta)|}{|2\sin\left(\frac{\phi – \theta}{2}\right)|}
$$
Therefore, the perpendicular distance from the origin to the given line is
$$
\boxed{d = \frac{|\sin(\phi – \theta)|}{|2\sin\left(\frac{\phi – \theta}{2}\right)|}}
$$
This problem involves coordinate geometry, trigonometric identities, and the formula for perpendicular distance from a point to a line in the form $Ax + By + C = 0$.
NCERT Question 5. Find the equation of the line parallel to the y-axis and drawn through the point of intersection of the lines $x – 7y + 5 = 0$ and $3x + y = 0$.
Solution:
The two given lines are
$$
x – 7y + 5 = 0 \quad \text{…(1)}
$$
$$
3x + y = 0 \quad \text{…(2)}
$$
From equation (2),
$$
y = -3x
$$
Substitute this in (1):
$$
x – 7(-3x) + 5 = 0
$$
$$
x + 21x + 5 = 0
$$
$$
22x = -5 \Rightarrow x = -\frac{5}{22}
$$
Now, substitute $x = -\dfrac{5}{22}$ in (2):
$$
3\left(-\frac{5}{22}\right) + y = 0
$$
$$
y = \frac{15}{22}
$$
Hence, the point of intersection is $\left(-\dfrac{5}{22}, \dfrac{15}{22}\right)$.
A line parallel to the y-axis has the form $x = a$.
Since it passes through $\left(-\dfrac{5}{22}, \dfrac{15}{22}\right)$,
$$
a = -\frac{5}{22}
$$
Therefore, the required equation of the line is
$$
\boxed{x = -\frac{5}{22}}
$$
This exercise uses concepts of slope, equations of lines, and parallel lines in Class 11 coordinate geometry topics from the NCERT Maths chapter on Straight Lines.
NCERT Question 6 : Find the equation of a line drawn perpendicular to the line $\dfrac{x}{4}+\dfrac{y}{6}=1$ through the point where it meets the $y$–axis.
Solution:
Given line:
$$\frac{x}{4}+\frac{y}{6}=1 \Rightarrow 3x+2y-12=0.$$
Rewriting,
$$y=-\frac{3}{2}x+6,$$
which is of the form $y=mx+c$.
Hence, slope of the given line $m=-\dfrac{3}{2}$.
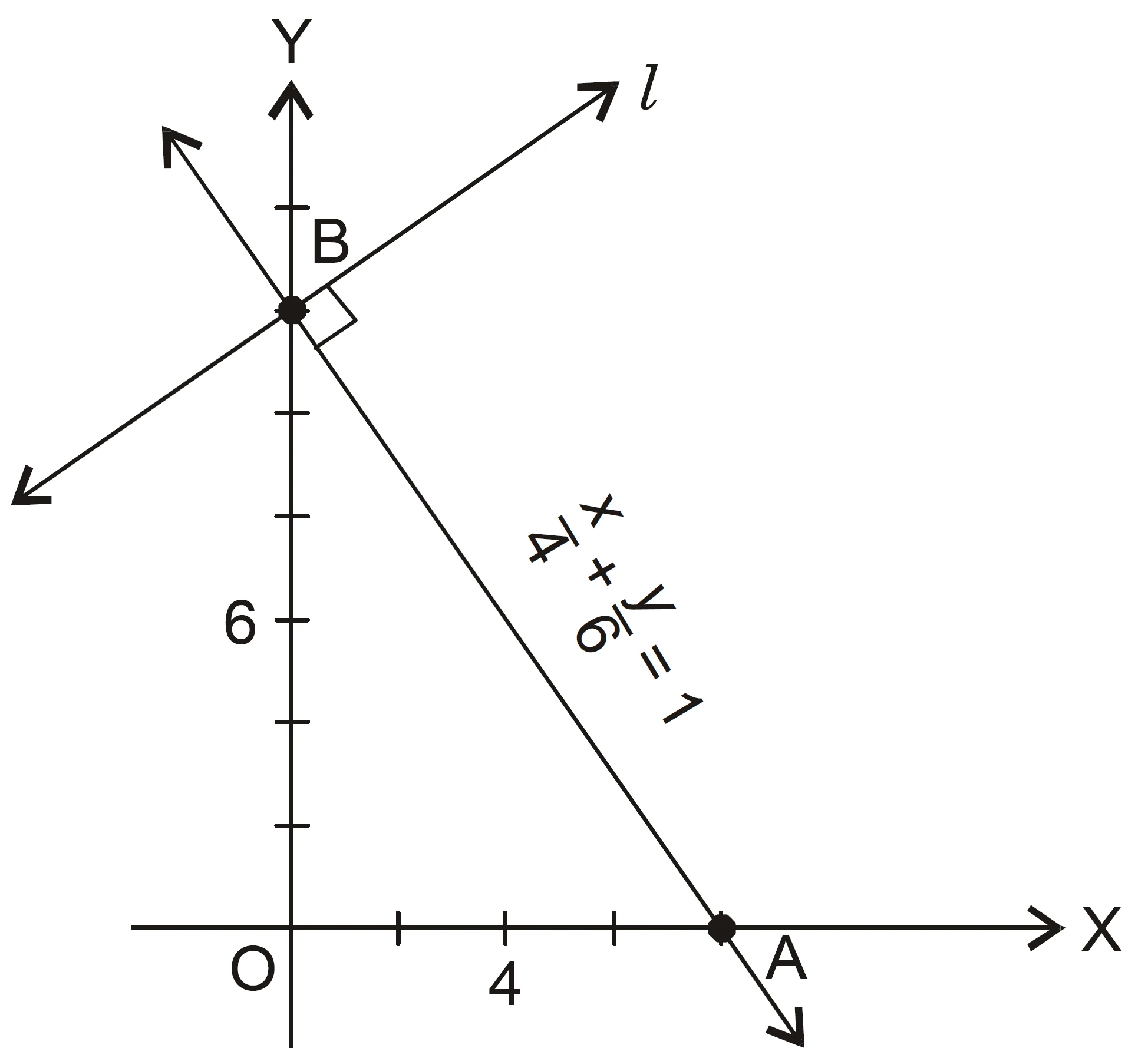
For a line perpendicular to it,
$$m_1 \times m_2=-1 \Rightarrow m_2=-\frac{1}{m_1}=\frac{2}{3}.$$
The given line meets the $y$–axis at $(0,6)$ because when $x=0$,
$$\frac{y}{6}=1 \Rightarrow y=6.$$
Equation of the required line passing through $(0,6)$ with slope $\frac{2}{3}$ is
$$(y-6)=\frac{2}{3}(x-0)$$
$$3y-18=2x$$
$$2x-3y+18=0.$$
$$\boxed{2x-3y+18=0}$$
(Concepts used: slope of perpendicular lines, intercept form, equation of line through a point)
Perpendicular line equation, slope-intercept form, coordinate geometry, class 11 maths, NCERT lines and angles, line passing through y-axis, equations of straight lines, Anand Classes NCERT solutions.
NCERT Question 7 : Find the area of the triangle formed by the lines $y-x=0$, $x+y=0$ and $x-k=0$.
Solution:
Given lines:
(1) $y-x=0$
(2) $x+y=0$
(3) $x-k=0$
Intersection points:
- (1) & (2): $(0,0)$
- (2) & (3): $(k,-k)$
- (3) & (1): $(k,k)$
So, vertices of the triangle are $(0,0)$, $(k,-k)$, and $(k,k)$.
Area of a triangle with vertices $(x_1,y_1)$, $(x_2,y_2)$, $(x_3,y_3)$ is
$$A=\frac{1}{2}|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|$$
Substitute:
$$A=\frac{1}{2}|0(-k-k)+k(k-0)+k(0-(-k))|$$
$$=\frac{1}{2}|k^2+k^2|$$
$$=\frac{1}{2}\times2k^2=k^2.$$
$$\boxed{A=k^2\ \text{square units}}$$
(Concepts used: area of triangle by coordinate geometry, intersection of lines, coordinate geometry formulas)
Area of triangle using coordinates, intersection of lines, coordinate geometry NCERT class 11, straight line equations, geometry formula derivation, Anand Classes NCERT coordinate geometry solutions.
NCERT Question 8 : Find the value of $p$ so that the three lines $3x + y – 2 = 0$, $px + 2y – 3 = 0$ and $2x – y – 3 = 0$ may intersect at one point.
Solution:
It is given that
$$3x + y – 2 = 0 \quad \text{(1)}$$
$$px + 2y – 3 = 0 \quad \text{(2)}$$
$$2x – y – 3 = 0 \quad \text{(3)}$$
By solving equations (1) and (3), we get
$$x = 1 \quad \text{and} \quad y = -1$$
Since the three lines intersect at one point, the point of intersection of lines (1) and (3) will also satisfy line (2).
Substitute $(x, y) = (1, -1)$ in equation (2):
$$p(1) + 2(-1) – 3 = 0$$
$$p – 2 – 3 = 0$$
$$p = 5$$
Therefore, the value of p is 5.
This solution helps in understanding concurrent lines, pair of linear equations, and coordinate geometry concepts from NCERT Class 11.
Download the complete NCERT Maths solutions by Anand Classes for practice and board exam preparation for IIT JEE, NDA, and CUET aspirants.
NCERT Question 9 : If three lines whose equations are $y = m_1x + c_1$, $y = m_2x + c_2$ and $y = m_3x + c_3$ are concurrent, then show that
$$m_1(c_2 – c_3) + m_2(c_3 – c_1) + m_3(c_1 – c_2) = 0.$$
Solution:
It is given that
$$y = m_1x + c_1 \quad \text{(1)}$$
$$y = m_2x + c_2 \quad \text{(2)}$$
$$y = m_3x + c_3 \quad \text{(3)}$$
By subtracting equation (1) from (2), we get
$$0 = (m_2 – m_1)x + (c_2 – c_1)$$
$$\Rightarrow (m_1 – m_2)x = c_2 – c_1$$
$$\Rightarrow x = \frac{c_2 – c_1}{m_1 – m_2}$$
Substitute this value of $x$ in equation (1):
$$y = m_1x + c_1$$
$$y = \frac{m_1(c_2 – c_1)}{m_1 – m_2} + c_1$$
$$y = \frac{m_1c_2 – m_2c_1}{m_1 – m_2}$$
Hence,
$$P\left(\frac{c_2 – c_1}{m_1 – m_2}, \frac{m_1c_2 – m_2c_1}{m_1 – m_2}\right)$$
is the point of intersection of lines (1) and (2).
Since the three lines are concurrent, this point $P\left(\dfrac{c_2 – c_1}{m_1 – m_2}, \dfrac{m_1c_2 – m_2c_1}{m_1 – m_2}\right)$ must satisfy equation (3):
$$y = m_3x + c_3$$
$$\frac{m_1c_2 – m_2c_1}{m_1 – m_2} = \frac{m_3(c_2 – c_1)}{m_1 – m_2} + c_3$$
Simplifying,
$$m_1c_2 – m_2c_1 – m_3c_2 + m_3c_1 – m_1c_3 + m_2c_3 = 0$$
$$\Rightarrow m_1(c_2 – c_3) + m_2(c_3 – c_1) + m_3(c_1 – c_2) = 0$$
Hence proved.
Concepts used: Concurrent lines, slope-intercept form, coordinate geometry formulas.
For more NCERT Maths Chapter 10 Line and Pair of Lines explanations, download detailed solutions by Anand Classes for Class 11 Maths, JEE Main, NDA, and CUET preparation.
NCERT Question 10 : Find the equation of the lines through the point $(3, 2)$ which makes an angle of $45^\circ$ with the line $x – 2y = 3$.
Solution:
Suppose $m_2$ is the slope of the line passing through the point $(3, 2)$.
The given line $l$ is $x – 2y = 3$, which can be written in slope-intercept form as
$$
y = \frac{1}{2}x – \frac{3}{2}
$$
So the slope of the given line is $m_1 = \dfrac{1}{2}$.
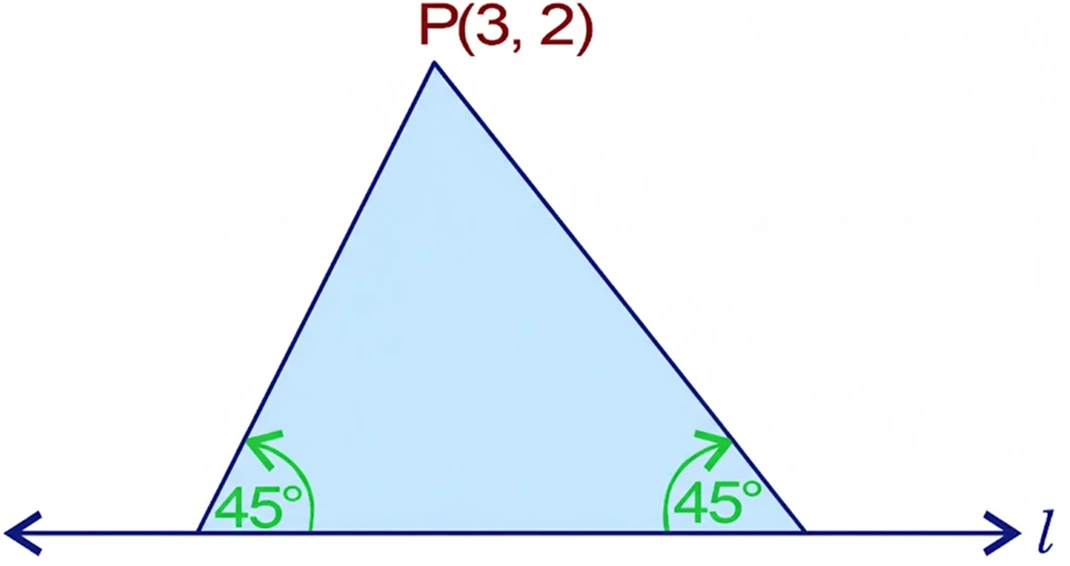
The angle between the required line and the given line is $45^\circ$, so
$$
\tan \theta = \left| \frac{m_1 – m_2}{1 + m_1 m_2 } \right|
$$
Substitute the values:
$$
1 = \left| \frac{\dfrac{1}{2} – m_2}{1 + \dfrac{m_2}{2}} \right|
$$
Simplifying:
$$
\frac{1 – 2m_2}{2 + m_2} = \pm 1
$$
Solve for $m_2$:
- $2 + m_2 = 1 – 2m_2 \implies 3m_2 = -1 \implies m_2 = -\frac{1}{3}$
- $2 + m_2 = -1 + 2m_2 \implies m_2 = 3$
Now find the equations:
Case 1: $m_2 = 3$
$$
y – 2 = 3(x – 3) \implies y – 2 = 3x – 9 \implies 3x – y = 7
$$
Case 2: $m_2 = -\dfrac{1}{3}$
$$
y – 2 = -\frac{1}{3}(x – 3) \implies 3y – 6 = -x + 3 \implies x + 3y = 9
$$
Answer:
The equations of the lines are
$$
3x – y = 7 \quad \text{and} \quad x + 3y = 9
$$
Download detailed NCERT solutions by Anand Classes for Class 11 Maths, JEE Main, NDA, and CUET preparation.
NCERT Question 11 : Find the equation of the line passing through the point of intersection of the lines $4x + 7y – 3 = 0$ and $2x – 3y + 1 = 0$ that has equal intercepts on the axes.
Solution:
The equation of a line having equal intercepts on the axes is
$$
\frac{x}{a} + \frac{y}{a} = 1 \implies x + y = a \quad \text{(1)}
$$
Find the point of intersection of the two given lines:
$$
4x + 7y – 3 = 0, \quad 2x – 3y + 1 = 0
$$
Solving simultaneously:
$$
x = \frac{1}{13}, \quad y = \frac{5}{13}
$$
Substitute $(x, y) = (1/13, 5/13)$ into equation (1):
$$
\frac{1}{13} + \frac{5}{13} = a \implies a = \frac{6}{13}
$$
Thus, the equation becomes
$$
x + y = \frac{6}{13} \implies 13x + 13y = 6
$$
Answer:
The required line is
$$
13x + 13y = 6
$$
Download detailed NCERT solutions by Anand Classes for Class 11 Maths, JEE Main, NDA, and CUET preparation.
NCERT Question 12 : Show that the equation of the line passing through the origin and making an angle $\theta$ with the line $y = mx + c$ is
$$
\dfrac{y}{x} = \dfrac{m \pm \tan \theta}{1 \mp m \tan \theta}.
$$
Solution:
Suppose the line passing through the origin is $y = m_1 x$. Hence, its slope is
$$
m_1 = \dfrac{y}{x}.
$$
The given line is $y = mx + c$ with slope $m$, and it makes an angle $\theta$ with the line $y = m_1 x$.
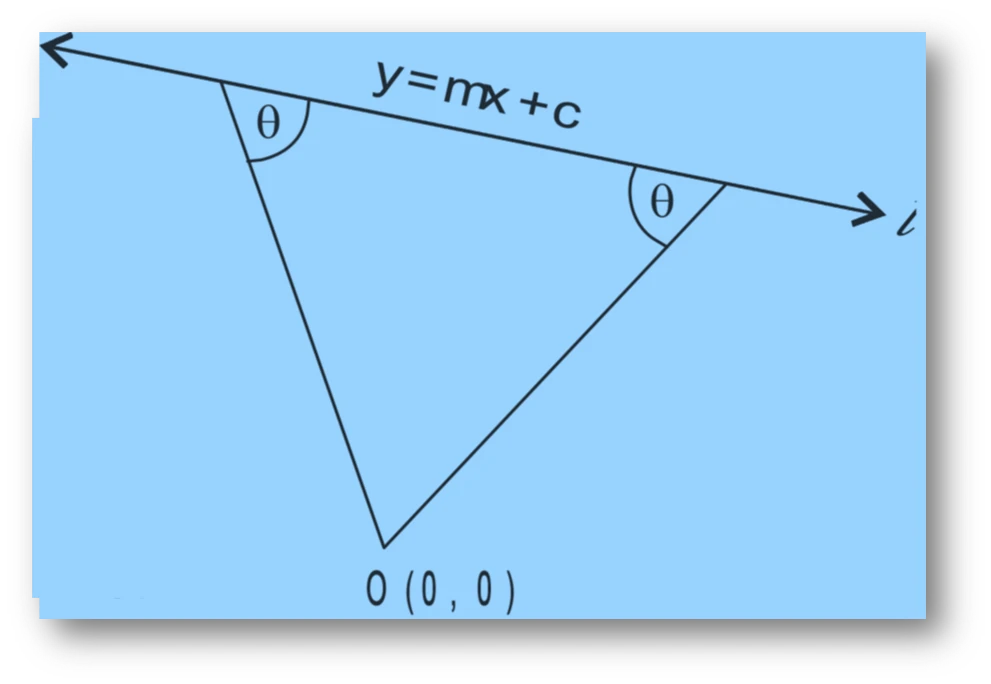
The angle between two lines is given by
$$
\tan \theta = \left| \dfrac{m_1 – m}{1 + m_1 m} \right|.
$$
Substitute $m_1 = \dfrac{y}{x}$:
$$
\tan \theta = \left| \dfrac{\frac{y}{x} – m}{1 + m \dfrac{y}{x}} \right|.
$$
Solving, we get two cases:
- $\dfrac{y}{x}(1 – m \tan \theta) = m + \tan \theta \implies \dfrac{y}{x} = \dfrac{m + \tan \theta}{1 – m \tan \theta}$
- $\dfrac{y}{x}(1 + m \tan \theta) = m – \tan \theta \implies \dfrac{y}{x} = \dfrac{m – \tan \theta}{1 + m \tan \theta}$
Hence,
$$
\dfrac{y}{x} = \dfrac{m \pm \tan \theta}{1 \mp m \tan \theta}.
$$
Hence proved.
Download detailed NCERT solutions by Anand Classes for Class 11 Maths, JEE Main, NDA, and CUET preparation.
NCERT Question.13 : In what ratio does the line joining $(-1, 1)$ and $(5, 7)$ get divided by the line $x + y = 4$?
Solution :
Let the point of intersection be $R$ which divides $PQ$ (where $P(-1,1)$ and $Q(5,7)$) in the ratio $k:1$.
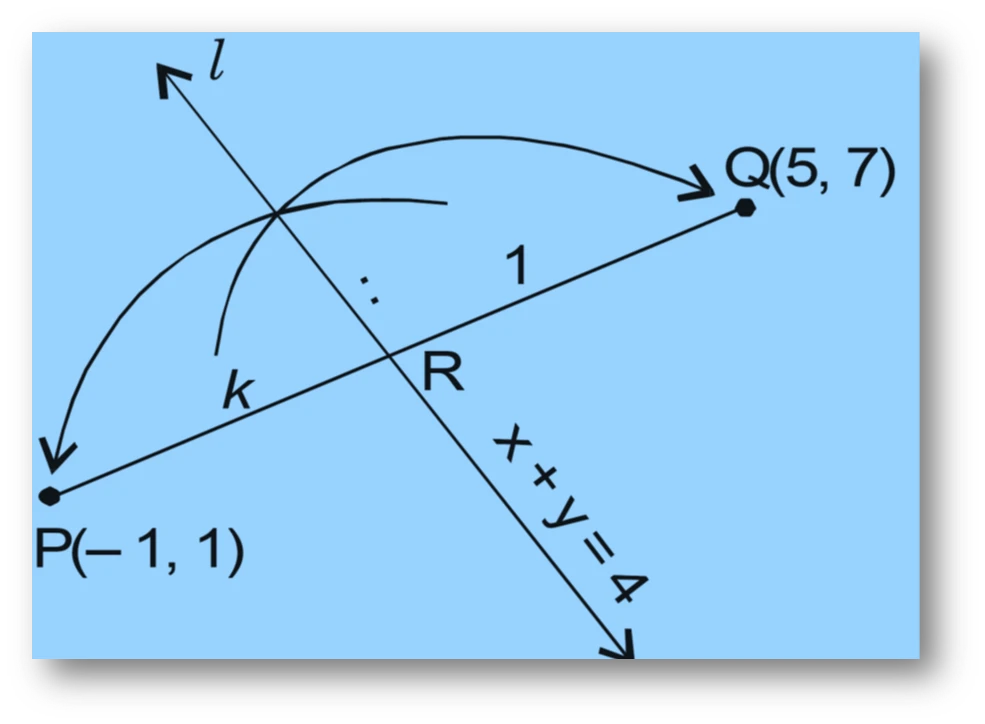
By the section formula,
$$
R = \left( \frac{k(-1) + 1(5)}{k + 1}, \frac{k(1) + 1(7)}{k + 1} \right)
= \left( \frac{5 – k}{k + 1}, \frac{k + 7}{k + 1} \right)
$$
Since $R$ lies on $x + y = 4$, we have
$$
\frac{5 – k}{k + 1} + \frac{k + 7}{k + 1} = 4
$$
Simplify:
$$
\frac{12}{k + 1} = 4
$$
Hence,
$$
12 = 4(k + 1) \Rightarrow 12 = 4k + 4 \Rightarrow 8k = 4 \Rightarrow k = \frac{1}{2}
$$
Therefore, the required ratio is $k:1 = \frac{1}{2}:1 = 1:2$.
Download detailed NCERT solutions by Anand Classes for Class 11 Maths, JEE Main, NDA, and CUET preparation.
NCERT Question.14 : Find the distance of the line $4x + 7y + 5 = 0$ from the point $(1, 2)$ along the line $2x – y = 0$.
Solution :
Point $P(1, 2)$ lies on the line $2x – y = 0$ (check: $2(1) – 2 = 0$).
Let $Q$ be the intersection point of two lines $4x + 7y + 5 = 0$ and $2x – y = 0$.
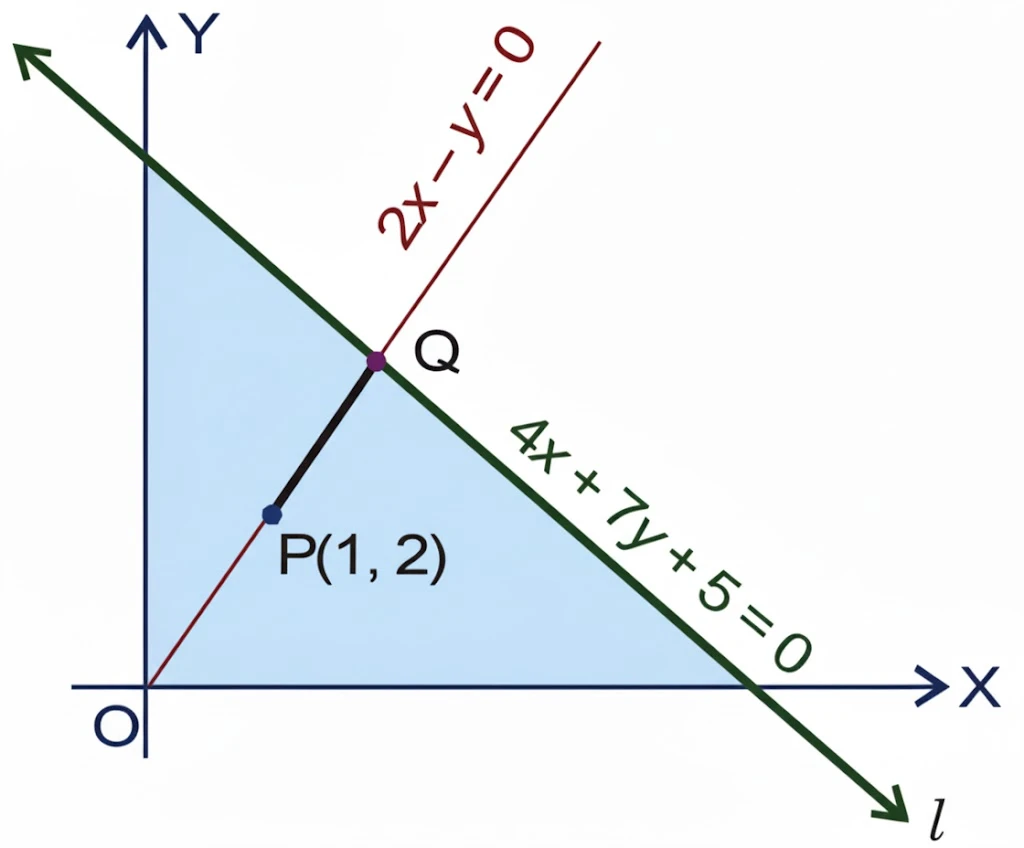
From $2x – y = 0$, we have $y = 2x$.
Substitute in $4x + 7y + 5 = 0$:
$$
4x + 7(2x) + 5 = 0 \Rightarrow 18x + 5 = 0 \Rightarrow x = -\frac{5}{18}
$$
Thus,
$$
y = 2x = -\dfrac{5}{9}
$$
So $Q\left(-\dfrac{5}{18}, -\dfrac{5}{9}\right)$.
Now, the distance between $P(1, 2)$ and $Q\left(-\dfrac{5}{18}, -\dfrac{5}{9}\right)$ is
$$
PQ = \sqrt{ \left(1 – \left(-\dfrac{5}{18}\right)\right)^2 + \left(2 – \left(-\dfrac{5}{9}\right)\right)^2 }
$$
Simplify:
$$
PQ = \sqrt{ \left(\frac{23}{18}\right)^2 + \left(\frac{23}{9}\right)^2 }
= 23 \sqrt{ \left(\frac{1}{18}\right)^2 + \left(\frac{1}{9}\right)^2 }
$$
$$
= 23 \sqrt{ \frac{1}{324} + \frac{4}{324} }
= 23 \sqrt{ \frac{5}{324} }
= \frac{23\sqrt{5}}{18}
$$
Hence, the required distance is $\displaystyle \frac{23\sqrt{5}}{18}$ units.
Download detailed NCERT solutions by Anand Classes for Class 11 Maths, JEE Main, NDA, and CUET preparation.
NCERT Question.15 : Find the direction in which a straight line must be drawn through the point $(-1, 2)$ so that its point of intersection with the line $x + y = 4$ may be at a distance of $3$ units from this point.
Solution :
Let the required line through $P(-1, 2)$ meet the line $x + y = 4$ at $(h, k)$.
Then the point $(h, k)$ satisfies
$$
h + k = 4 \quad \text{…(i)}
$$
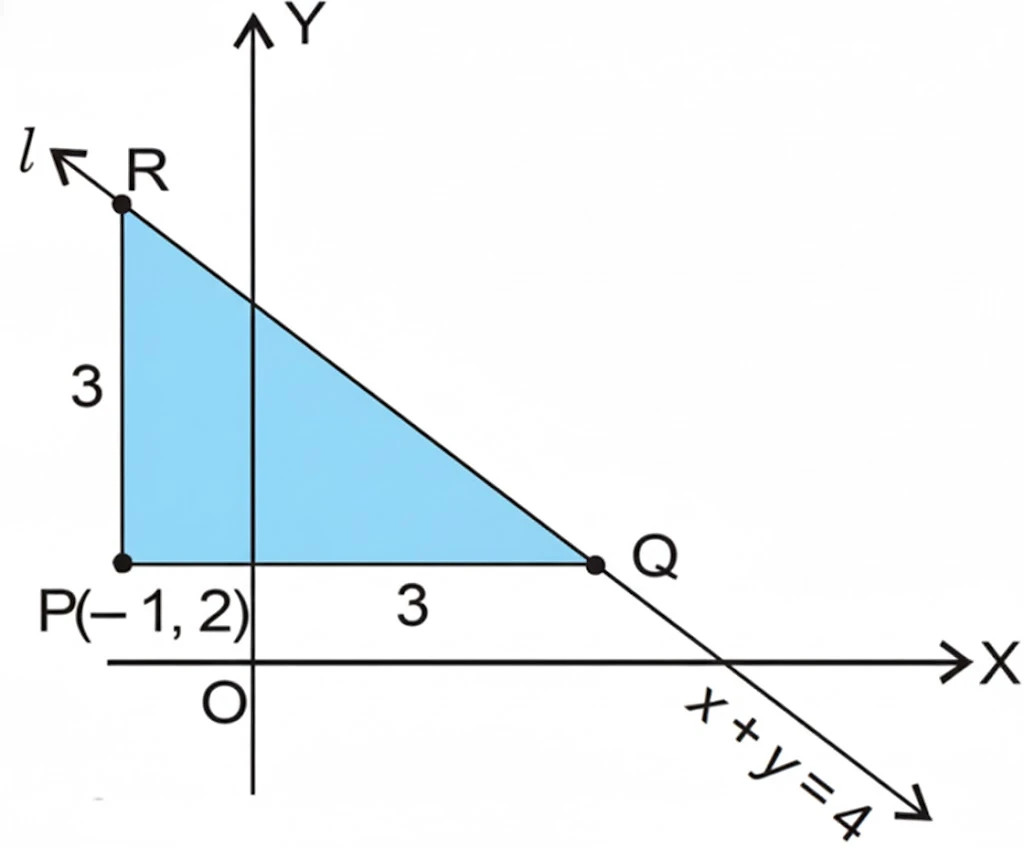
The distance between $(-1, 2)$ and $(h, k)$ is $3$.
So,
$$
\sqrt{(h + 1)^2 + (k – 2)^2} = 3
$$
Putting $k = 4 – h$ from (i),
$$
\sqrt{(h + 1)^2 + (2 – h)^2} = 3
$$
Squaring both sides:
$$
(h + 1)^2 + (2 – h)^2 = 9
$$
Expanding,
$$
h^2 + 2h + 1 + h^2 – 4h + 4 = 9
$$
Simplifying,
$$
2h^2 – 2h – 4 = 0
$$
Dividing by $2$:
$$
h^2 – h – 2 = 0
$$
So,
$$
(h – 2)(h + 1) = 0
$$
Hence, $h = 2$ or $h = -1$.
When $h = 2$, then $k = 4 – 2 = 2$.
When $h = -1$, then $k = 4 – (-1) = 5$.
Therefore, the two points of intersection are $Q(2, 2)$ and $R(-1, 5)$.
Now,
Slope of $PQ$:
$$
m_{PQ} = \frac{2 – 2}{2 – (-1)} = 0
$$
∴ $PQ$ is parallel to the $x$-axis.
Slope of $PR$:
$$
m_{PR} = \frac{5 – 2}{-1 – (-1)} = \frac{3}{0} = \infty
$$
∴ $PR$ is parallel to the $y$-axis.
Hence, the required line is parallel to the x-axis or the y-axis.
$$
\boxed{y = 2 \quad \text{or} \quad x = -1}
$$
Download detailed NCERT solutions by Anand Classes, the best coaching center for Class 11 Maths, IIT JEE, NDA, and CUET preparation.
NCERT Question.16 : The hypotenuse of a right-angled triangle has its ends at the points $(1, 3)$ and $(-4, 1)$. Find the equations of the legs (perpendicular sides) of the triangle.
Solution :
Let the ends of the hypotenuse be $A(1, 3)$ and $B(-4, 1)$, and the third vertex be $C(h, k)$.
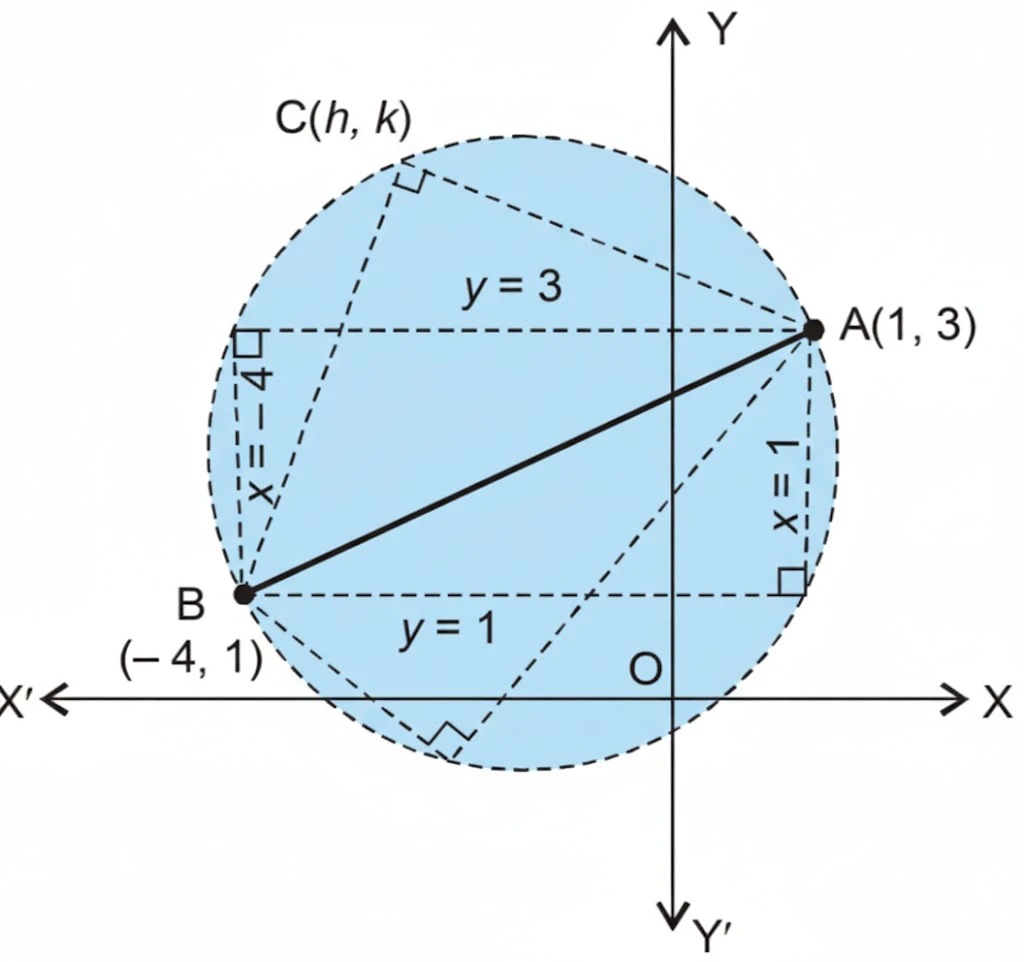
Since $\angle ACB = 90^\circ$,
Slope of $AC$:
$$
m_1 = \frac{k – 3}{h – 1}
$$
Slope of $BC$:
$$
m_2 = \frac{k – 1}{h + 4}
$$
For perpendicular lines, $m_1 \cdot m_2 = -1$:
$$
\frac{(k – 3)(k – 1)}{(h – 1)(h + 4)} = -1
$$
Simplifying,
$$
(h – 1)(h + 4) + (k – 3)(k – 1) = 0 \quad \text{…(iii)}
$$
This equation represents the locus of all possible points $C$ forming a right-angled triangle with hypotenuse $AB$.
Let $h = 1$ and $k = 1$, which satisfy (iii).
Then,
For $A(1, 3)$ and $C(1, 1)$:
$$
m_{AC} = \frac{1 – 3}{1 – 1} = \frac{-2}{0} = \text{undefined}
$$
∴ Line $AC$ is parallel to the $y$-axis.
Hence, equation of $AC$:
$$
x = 1
$$
For $B(-4, 1)$ and $C(1, 1)$:
$$
m_{BC} = \frac{1 – 1}{1 + 4} = 0
$$
∴ Line $BC$ is parallel to the $x$-axis.
Hence, equation of $BC$:
$$
y = 1
$$
Therefore, the equations of the two perpendicular sides are
$$
\boxed{x = 1 \quad \text{and} \quad y = 1}
$$
Remark:
$C$ can be any point on the circle drawn with $AB$ as diameter.
For every such $C$, the coordinates satisfy equation (iii), hence there are infinitely many possible legs.
Download detailed NCERT solutions by Anand Classes, the best coaching center for Class 11 Maths, IIT JEE, NDA, and CUET preparation.
NCERT Question 17 : Find the image of the point $(3,8)$ with respect to the line $x+3y=7$ (the line acts as a plane mirror).
Solution :
Line (mirror):
$$x+3y-7=0.$$
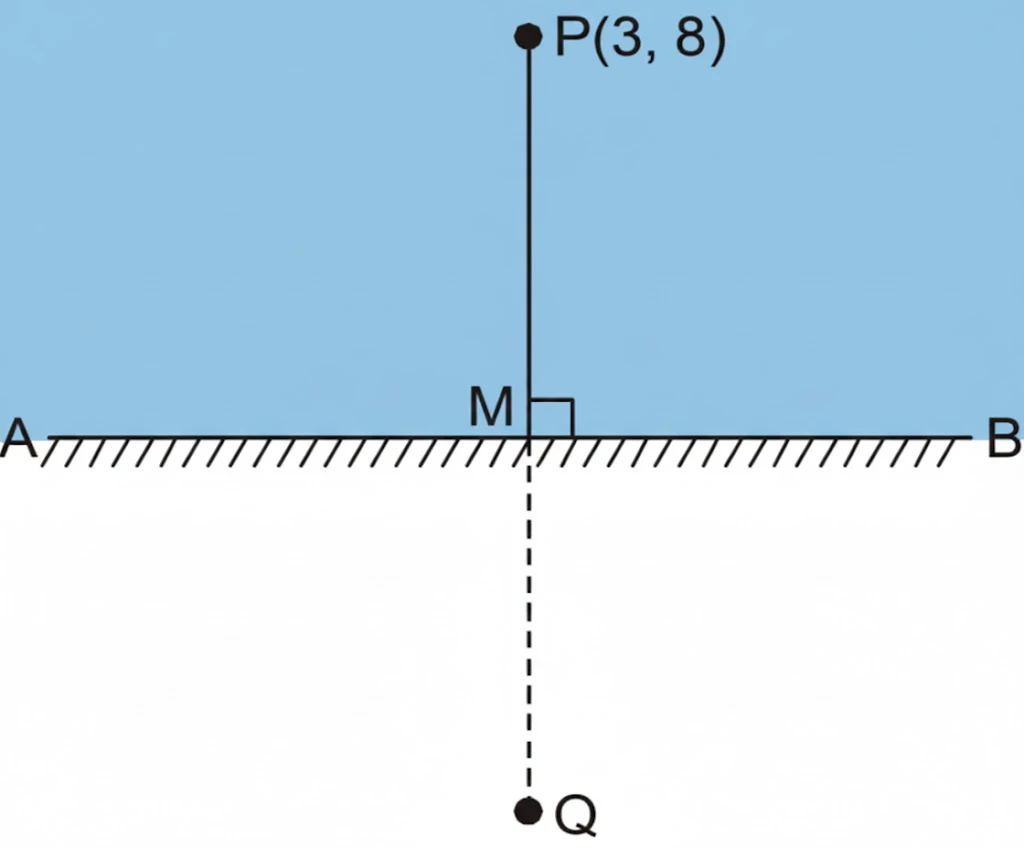
Given point $P(3,8)$. Let $M(x_0,y_0)$ be the foot of the perpendicular from $P$ to the line; $M$ is the midpoint of $P$ and its image $Q(\alpha,\beta)$.
Slope of mirror $= -\dfrac{1}{3}$, so slope of perpendicular $=3$. Equation of the perpendicular through $P(3,8)$:
$$y-8=3(x-3)\quad\Longrightarrow\quad 3x-y-1=0.$$
Find $M$ as intersection of
$$x+3y-7=0\quad\text{and}\quad 3x-y-1=0.$$
Solve above equations : multiply second by $3$ and add to first:
$$
x+3y-7 + 9x-3y-3 = 0 \implies 10x-10=0 \implies x=1.
$$
Then from $x+3y-7=0\implies$ $1+3y-7=0\implies y=2$.
So the foot is $M(1,2)$.
Since $M$ is midpoint of $P(3,8)$ and $Q(\alpha,\beta)$,
$$\frac{3+\alpha}{2}=1,\qquad \frac{8+\beta}{2}=2.$$
Hence $\alpha=-1,\ \beta=-4$.
Therefore the image point is
$$\boxed{Q(-1,-4)}.$$
Download detailed NCERT solutions by Anand Classes for Class 11 Maths, JEE Main, NDA, and CUET preparation.
NCERT Question 18 : If the lines $y=3x+1$ and $2y=x+3$ are equally inclined to the line $y=mx+4$, find the value(s) of $m$.
Solution :
Slopes: $m_1=3$, $m_2=\dfrac{1}{2}$ (since $2y=x+3\Rightarrow y=\dfrac{x}{2}+\dfrac{3}{2}$), and the third line has slope $m$.
Equal inclination means the (acute) angles between line$(m_1)$ and line$(m)$ and between line$(m_2)$ and line$(m)$ are equal in magnitude. Using the formula for angle between lines,
$$
\left|\frac{m_1-m}{1+m_1m}\right|=\left|\frac{m_2-m}{1+m_2m}\right|.
$$
This gives two cases (±). Taking the sign that yields real solutions leads to
$$
\frac{3-m}{1+3m} = -\frac{\dfrac12-m}{1+\dfrac m2}
$$
Cross-multiplying and simplifying produces the quadratic
$$7m^2-2m-7=0.$$
Solving,
$$
m=\frac{1\pm 5\sqrt{2}}{7}.
$$
Thus the required values are
$$\boxed{m=\dfrac{1+5\sqrt{2}}{7}\quad\text{or}\quad m=\dfrac{1-5\sqrt{2}}{7}}.$$
Download detailed NCERT solutions by Anand Classes for Class 11 Maths, JEE Main, NDA, and CUET preparation.
NCERT Question 19 : If the sum of the perpendicular distances of a variable point $P(x, y)$ from the lines
$$x + y – 5 = 0 \quad \text{and} \quad 3x – 2y + 7 = 0$$
is always $10$, show that $P$ must move on a line.
Solution:
We know that the perpendicular distance of a line $Ax + By + C = 0$ from a point $(x, y)$ is given by
$$d = \frac{|Ax + By + C|}{\sqrt{A^2 + B^2}}.$$
Hence, for the given lines:
- For $x + y – 5 = 0$,
$$d_1 = \frac{|x + y – 5|}{\sqrt{1^2 + 1^2}} = \frac{|x + y – 5|}{\sqrt{2}}.$$ - For $3x – 2y + 7 = 0$,
$$d_2 = \frac{|3x – 2y + 7|}{\sqrt{3^2 + (-2)^2}} = \frac{|3x – 2y + 7|}{\sqrt{13}}.$$
According to the question,
$$d_1 + d_2 = 10.$$
Substituting the values of $d_1$ and $d_2$,
$$\frac{|x + y – 5|}{\sqrt{2}} + \frac{|3x – 2y + 7|}{\sqrt{13}} = 10.$$
Multiplying both sides by $\sqrt{26}$ to clear denominators,
$$\sqrt{13} |x + y – 5| + \sqrt{2} |3x – 2y + 7| = 10\sqrt{26}.$$
Assuming both expressions inside the modulus are positive (a valid branch),
$$\sqrt{13}(x + y – 5) + \sqrt{2}(3x – 2y + 7) = 10\sqrt{26}.$$
Expanding,
$$\sqrt{13}x + \sqrt{13}y – 5\sqrt{13} + 3\sqrt{2}x – 2\sqrt{2}y + 7\sqrt{2} – 10\sqrt{26} = 0.$$
Grouping like terms,
$$(\sqrt{13} + 3\sqrt{2})x + (\sqrt{13} – 2\sqrt{2})y + (7\sqrt{2} – 5\sqrt{13} – 10\sqrt{26}) = 0.$$
This is a linear equation in $x$ and $y$, hence it represents a line.
Therefore, $P$ must move on a line.
Hence proved.
NCERT Question 20 : Find the equation of the line which is equidistant from the parallel lines $$9x + 6y – 7 = 0 \quad \text{and} \quad 3x + 2y + 6 = 0$$
Solution:
Let $(a, b)$ be a point on the required line.
The perpendicular distance of a line $Ax + By + C = 0$ from $(x, y)$ is given by
$$d = \frac{|Ax + By + C|}{\sqrt{A^2 + B^2}}.$$
Hence, for the two given lines:
- From $9x + 6y – 7 = 0$:
$$d_1 = \frac{|9a + 6b – 7|}{\sqrt{9^2 + 6^2}} = \frac{|9a + 6b – 7|}{3\sqrt{13}}.$$ - From $3x + 2y + 6 = 0$:
$$d_2 = \frac{|3a + 2b + 6|}{\sqrt{3^2 + 2^2}} = \frac{|3a + 2b + 6|}{\sqrt{13}}.$$
Since the required line is equidistant from both,
$$d_1 = d_2.$$
Therefore,
$$\frac{|9a + 6b – 7|}{3\sqrt{13}} = \frac{|3a + 2b + 6|}{\sqrt{13}}.$$
Simplifying,
$$|9a + 6b – 7| = 3|3a + 2b + 6|.$$
Now, consider the two possible cases for the modulus expressions.
Case 1:
$$9a + 6b – 7 = 3(3a + 2b + 6)$$
$$\Rightarrow 9a + 6b – 7 = 9a + 6b + 18$$
$$\Rightarrow -7 = 18$$
which is not possible.
Case 2:
$$9a + 6b – 7 = -3(3a + 2b + 6)$$
$$\Rightarrow 9a + 6b – 7 = -9a – 6b – 18$$
$$\Rightarrow 18a + 12b + 11 = 0.$$
Hence, the equation of the required line is
$$\boxed{18x + 12y + 11 = 0}.$$
Download detailed NCERT solutions by Anand Classes for Class 11 Maths, JEE Main, NDA, and CUET preparation.
NCERT Question.21 : A ray of light passing through the point $(1, 2)$ reflects on the x-axis at point $A$ and the reflected ray passes through the point $(5, 3)$. Find the coordinates of $A$.
Solution :
Let the coordinates of point $A$ on the x-axis be $(\alpha, 0)$. Let the incident ray $PA$, where $P$ is $(1, 2)$, make an angle $\theta$ with the normal $AN$, then the reflected ray $AQ$, where $Q$ is $(5, 3)$, also makes angle $\theta$ with the normal $AN$ (by the Law of Reflection).
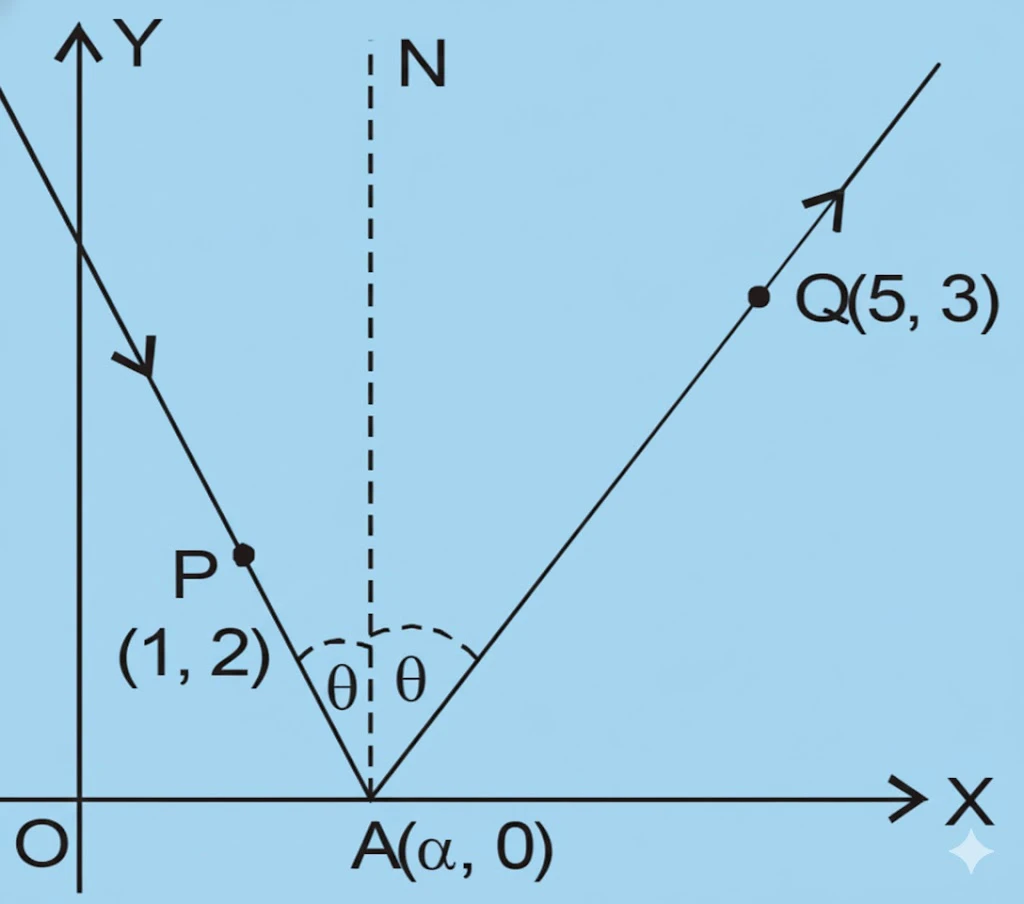
Since
$$\angle XA Q = 90^\circ – \theta \quad \text{and} \quad \angle XAP = 90^\circ + \theta,$$
we have:
- Slope of $AQ = \tan(90^\circ – \theta) = \cot \theta$
- Slope of $AP = \tan(90^\circ + \theta) = -\cot \theta$
Thus,
$$\text{Slope of } AQ + \text{Slope of } AP = 0$$
Now, the slope formulas give:
$$\frac{3 – 0}{5 – \alpha} + \frac{2 – 0}{1 – \alpha} = 0$$
Simplifying:
$$\frac{3}{5 – \alpha} + \frac{2}{1 – \alpha} = 0$$
Cross-multiplying:
$$3(1 – \alpha) + 2(5 – \alpha) = 0$$
$$3 – 3\alpha + 10 – 2\alpha = 0$$
$$-5\alpha + 13 = 0 \quad \Rightarrow \quad \alpha = \frac{13}{5}$$
Hence, the coordinates of $A$ are:
$$(\alpha, 0) = \left(\frac{13}{5}, 0\right)$$
Download detailed NCERT solutions by Anand Classes for Class 11 Maths, JEE Main, NDA, and CUET preparation.
NCERT Question.22 : Prove that the product of the lengths of the perpendiculars drawn from the points $(\sqrt{a^2-b^2},0)$ and $(-\sqrt{a^2-b^2},0)$ to the line $\dfrac{x}{a}\cos\theta + \dfrac{y}{b}\sin\theta = 1$ is $b^2$.
Solution :
We are given the line:
$\dfrac{x}{a}\cos\theta + \dfrac{y}{b}\sin\theta = 1 \Rightarrow b x \cos\theta + a y \sin\theta – ab = 0 \quad (1)$
The perpendicular distance $d$ of a line $Ax + By + C = 0$ from a point $(x_0, y_0)$ is given by:
$$d = \dfrac{|A x_0 + B y_0 + C|}{\sqrt{A^2 + B^2}}$$
So, the perpendicular distance $d_1$ of line (1) from the point $(\sqrt{a^2-b^2}, 0)$ is:
$$
d_1 = \dfrac{|b \cos\theta \sqrt{a^2-b^2} + a \sin\theta \cdot 0 – ab|}{\sqrt{b^2 \cos^2\theta + a^2 \sin^2\theta}} $$
$$
d_1 = \dfrac{|b \cos\theta \sqrt{a^2-b^2} – ab|}{\sqrt{b^2 \cos^2\theta + a^2 \sin^2\theta}}$$
Similarly, the perpendicular distance $d_2$ from the point $(-\sqrt{a^2-b^2}, 0)$ is:
$$
d_2 = \frac{|b \cos\theta (-\sqrt{a^2-b^2}) + a \sin\theta \cdot 0 – ab|}{\sqrt{b^2 \cos^2\theta + a^2 \sin^2\theta}} $$
$$
d_2 = \frac{|b \cos\theta \sqrt{a^2-b^2} + ab|}{\sqrt{b^2 \cos^2\theta + a^2 \sin^2\theta}}$$
Now, the product of the perpendiculars is:
$$d_1 d_2 = \dfrac{|b \cos\theta \sqrt{a^2-b^2} – ab|}{\sqrt{b^2 \cos^2\theta + a^2 \sin^2\theta}} \cdot \dfrac{|b \cos\theta \sqrt{a^2-b^2} + ab|}{\sqrt{b^2 \cos^2\theta + a^2 \sin^2\theta}}$$
$$d_1 d_2 = \dfrac{|(b \cos\theta \sqrt{a^2-b^2})^2 – (ab)^2|}{b^2 \cos^2\theta + a^2 \sin^2\theta} $$
$$d_1 d_2 = \dfrac{b^2 | \cos^2\theta (a^2 – b^2) – a^2 |}{b^2 \cos^2\theta + a^2 \sin^2\theta}$$
$$d_1 d_2 = \dfrac{b^2 | a^2 (\cos^2\theta – 1) – b^2 \cos^2\theta |}{b^2 \cos^2\theta + a^2 \sin^2\theta} $$
$$d_1 d_2 = \dfrac{b^2 |-a^2 \sin^2\theta – b^2 \cos^2\theta|}{b^2 \cos^2\theta + a^2 \sin^2\theta}$$
$$d_1 d_2 = \dfrac{b^2 (b^2 \cos^2\theta + a^2 \sin^2\theta)}{b^2 \cos^2\theta + a^2 \sin^2\theta} = b^2$$
Hence, proved.
Online detailed NCERT solutions by Anand Classes for Class 11 Maths, JEE Main, NDA, and CUET preparation.
NCERT Question.23 : A person standing at the junction (crossing) of two straight paths represented by the equations $2x – 3y + 4 = 0$ and $3x + 4y – 5 = 0$ wants to reach the path whose equation is $6x – 7y + 8 = 0$ in the least time. Find the equation of the path that he should follow.
Solution :
The person is standing at point P which is the point of intersection of lines $2x – 3y + 4 = 0$ and $3x + 4y – 5 = 0$.
Solving these equations gives coordinates of point P:
$$ x = -\dfrac{1}{17}, \quad y = \dfrac{22}{17} $$
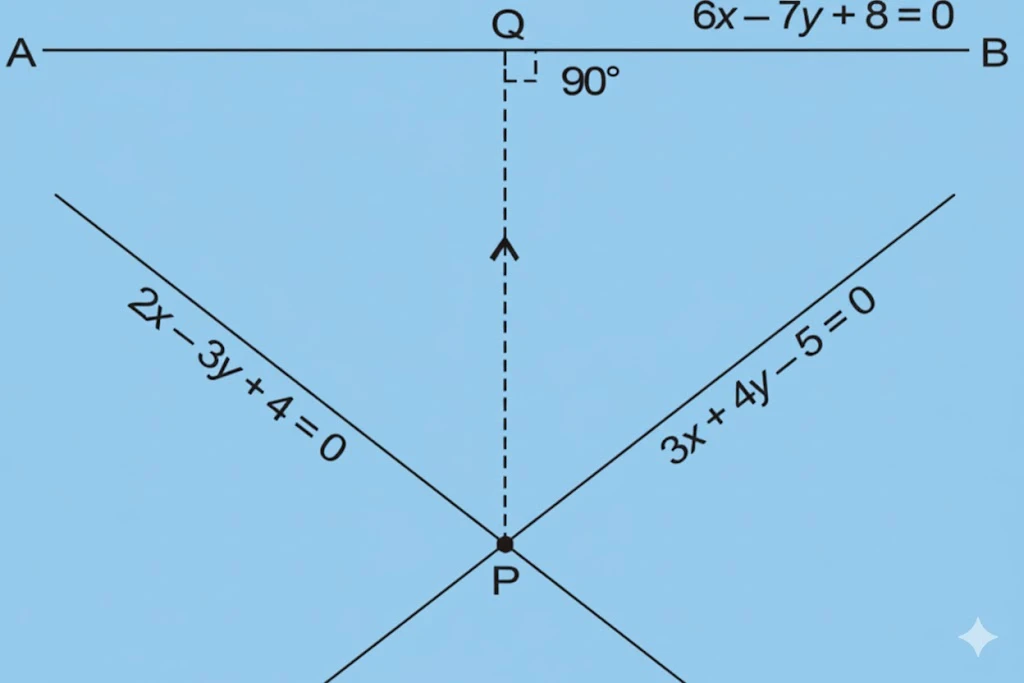
The shortest distance is along the perpendicular path PQ to the line AB whose equation is $6x – 7y + 8 = 0$ from the point $P(-\dfrac{1}{17}, \dfrac{22}{17})$.
- Slope of line AB : $6x – 7y + 8 = 0$ is $6/7$
- Slope of perpendicular line PQ : $-7/6$
Equation of the perpendicular line PQ passing through $P(-\dfrac{1}{17}, \dfrac{22}{17})$:
$$y – \dfrac{22}{17} = -\dfrac{7}{6} (x + \dfrac{1}{17})$$
On solving :
$$6 (17y – 22) = -7 (17x + 1)$$
$$102y – 132 = -119x – 7$$
$$119x + 102y = 125$$
Hence, the required path is $119x + 102y = 125$.
Download detailed NCERT solutions by Anand Classes for Class 11 Maths, JEE Main, NDA, and CUET preparation.


