Anand Classes provides NCERT Solutions for Class 11 Maths Chapter 9 – Straight Lines (Exercise 9.3) for the 2025–2026 academic session, strictly following the latest NCERT and CBSE guidelines. This exercise deals with important concepts such as distance of a point from a line, perpendicular and parallel lines, angle between two lines, and various forms of line equations. Each question is explained in a step-by-step manner with clear reasoning and formulas, ensuring students develop a strong understanding of coordinate geometry. These solutions are highly useful for CBSE Class 11 exams, and also for JEE Main, JEE Advanced, NDA, and CUET aspirants. Click the print button to download study material and notes in PDF format.
NCERT Question.1 : Reduce the following equations into slope–intercept form and find their slopes and the y–intercepts.
(i) (x + 7y = 0)
(ii) (6x + 3y – 5 = 0)
(iii) (y = 0)
Solution:
(i) Given equation:
$$x + 7y = 0$$
The slope–intercept form is represented as (y = mx + c), where (m) is the slope and (c) is the y–intercept.
Rewriting,
$$y = -\frac{1}{7}x + 0$$
Hence, the equation is in the form (y = mx + c), where ($m = -\frac{1}{7}$) and (c = 0).
Students preparing for Class 11 Coordinate Geometry can practice such problems for better conceptual clarity. For detailed step-by-step NCERT solutions, visit Anand Classes, the leading institute for IIT JEE and NDA coaching in India.
(ii) Given equation:
$$6x + 3y – 5 = 0$$
Rewriting in slope–intercept form (y = mx + c):
$$3y = -6x + 5$$
$$y = -2x + \frac{5}{3}$$
Hence, the equation is in the form (y = mx + c), where (m = -2) and ($c = \frac{5}{3}$).
For more Class 11 Maths Chapter 10 NCERT Solutions and practice questions on straight lines, download free study material from Anand Classes, the best coaching for CUET, IIT JEE, and NDA exams.
(iii) Given equation:
$$y = 0$$
This is already in slope–intercept form (y = mx + c):
$$y = 0x + 0$$
Hence, the equation is in the form (y = mx + c), where (m = 0) and (c = 0).
This simple form represents the x-axis equation in coordinate geometry. For complete NCERT notes and free PDF downloads, visit Anand Classes, trusted for Mathematics coaching and IIT JEE preparation.
NCERT Question.2 : Reduce the following equations into intercept form and find their intercepts on the axes.
(i) $3x + 2y – 12 = 0$
(ii) $4x – 3y = 6$
(iii) $3y + 2 = 0$
Solution:
(i) Given equation:
$$3x + 2y – 12 = 0 \implies 3x + 2y = 12$$
Equation in intercept form:
$$\frac{x}{4} + \frac{y}{6} = 1$$
Intercepts:
- $x$–axis intercept $a = 4$
- $y$–axis intercept $b = 6$
Coordinate geometry Class 11, x-axis y-axis intercepts, NCERT solutions by Anand Classes for IIT JEE and CUET preparation.
(ii) Given equation:
$$4x – 3y = 6$$
Dividing both sides by $6$:
$$\frac{4x}{6} – \frac{3y}{6} = 1 \implies \frac{2x}{3} – \frac{y}{2} = 1$$
Rewriting in intercept form:
$$\frac{x}{3/2} + \frac{y}{-2} = 1$$
Intercepts:
- $x$–axis intercept $a = \frac{3}{2}$
- $y$–axis intercept $b = -2$
Line equation in intercept form, NCERT Class 11 coordinate geometry, solutions by Anand Classes for NDA and IIT JEE.
(iii) Given equation:
$$3y + 2 = 0 \implies 3y = -2$$
Dividing by $-2$:
$$\frac{y}{-2/3} = 1$$
Intercepts:
- $x$–axis intercept $a = 0$
- $y$–axis intercept $b = -\frac{2}{3}$
Horizontal line y-intercept, Class 11 Maths coordinate geometry, NCERT solved examples by Anand Classes for CUET and competitive exams.
NCERT Question.3 : Find the distance of the point $(-1, 1)$ from the line $12(x + 6) = 5(y – 2)$
Solution:
Given line:
$$12(x + 6) = 5(y – 2)$$
Expanding:
$$12x + 72 = 5y – 10 \implies 12x – 5y + 82 = 0 \quad \text{(i)}$$
Comparing with $Ax + By + C = 0$, we get:
$$A = 12, \quad B = -5, \quad C = 82$$
Perpendicular distance of point $(x_1, y_1)$ from line $Ax + By + C = 0$ is:
$$d = \frac{|Ax_1 + By_1 + C|}{\sqrt{A^2 + B^2}}$$
Substituting $(x_1, y_1) = (-1, 1)$:
$$d = \frac{|12(-1) + (-5)(1) + 82|}{\sqrt{12^2 + (-5)^2}} = \frac{| -12 – 5 + 82 |}{\sqrt{144 + 25}} = \frac{65}{13} = 5$$
Hence, the distance is $5$ units.
NCERT Class 11 coordinate geometry solved examples by Anand Classes, helpful for IIT JEE, NDA, and CUET preparation.
Question.4 : Find the points on the x-axis whose distances from the line $\dfrac{x}{3} + \dfrac{y}{4} = 1$ are 4 units.
Solution:
Given line:
$$\frac{x}{3} + \frac{y}{4} = 1 \implies 4x + 3y = 12 \implies 4x + 3y – 12 = 0 \quad \text{(i)}$$
Comparing with $Ax + By + C = 0$, we get:
$$A = 4, \quad B = 3, \quad C = -12$$
Let the point on the x-axis be $(a, 0)$. The perpendicular distance formula gives:
$$d = \dfrac{|Ax_1 + By_1 + C|}{\sqrt{A^2 + B^2}}$$
Substituting $d = 4$ and $(x_1, y_1) = (a, 0)$:
$$4 = \dfrac{|4a + 3(0) – 12|}{\sqrt{4^2 + 3^2}} = \dfrac{|4a – 12|}{5}$$
$$|4a – 12| = 20 \implies 4a – 12 = 20 \text{ or } 4a – 12 = -20$$
$$4a = 32 \text{ or } 4a = -8 \implies a = 8 \text{ or } a = -2$$
Hence, the points are $(-2, 0)$ and $(8, 0)$.
Coordinate geometry exercises for Class 11, solved by Anand Classes for IIT JEE, NDA, and CUET aspirants.
NCERT Question.5 : Find the distance between parallel lines
(i) $15x + 8y – 34 = 0$ and $15x + 8y + 31 = 0$
(ii) $l(x + y) + p = 0$ and $l(x + y) – r = 0$
Solution:
(i) $15x + 8y – 34 = 0$ and $15x + 8y + 31 = 0$
For parallel lines $Ax + By + C_1 = 0$ and $Ax + By + C_2 = 0$, the distance $d$ is:
$$d = \frac{|C_1 – C_2|}{\sqrt{A^2 + B^2}}$$
Here, $A = 15, B = 8, C_1 = -34, C_2 = 31$. Substituting:
$$d = \frac{|-34 – 31|}{\sqrt{15^2 + 8^2}} = \frac{65}{\sqrt{225 + 64}} = \frac{65}{17}$$
Hence, the distance between the parallel lines is $\dfrac{65}{17}$.
(ii) $l(x + y) + p = 0$ and $l(x + y) – r = 0$
Rewriting:
$$lx + ly + p = 0, \quad lx + ly – r = 0$$
Distance formula for parallel lines:
$$d = \frac{|C_1 – C_2|}{\sqrt{A^2 + B^2}}$$
Here, $A = l, B = l, C_1 = p, C_2 = -r$. Substituting:
$$d = \frac{|p – (-r)|}{\sqrt{l^2 + l^2}} = \frac{|p + r|}{\sqrt{2} l}$$
Hence, the distance between these parallel lines is $\dfrac{|p + r|}{l\sqrt{2}}$.
Practice problems on distances between lines by Anand Classes for Class 11 coordinate geometry and competitive exams preparation like IIT JEE and CUET.
NCERT Question.6 : Find equation of the line parallel to the line $3x − 4y + 2 = 0$ and passing through the point $(-2, 3)$.
Solution:
The given line is:
$$3x – 4y + 2 = 0$$
Slope-intercept form:
$$y = \frac{3}{4}x + \frac{1}{2}$$
Slope of the given line: $m = \dfrac{3}{4}$
Parallel lines have the same slope. So the required line has slope $m = \dfrac{3}{4}$ and passes through $(-2, 3)$. Using point-slope form:
$$y – y_1 = m(x – x_1)$$
$$y – 3 = \frac{3}{4}(x + 2)$$
Multiply both sides by 4:
$$4y – 12 = 3x + 6$$
$$3x – 4y = -18$$
Hence, the equation of the required line is:
$$3x – 4y = -18$$
NCERT Question.7 :
Find equation of the line perpendicular to the line $x – 7y + 5 = 0$ and having x-intercept $3$.
Solution:
Given line:
$$x – 7y + 5 = 0$$
Slope-intercept form:
$$y = \frac{1}{7}x + \frac{5}{7}$$
Slope of the given line: $m = \dfrac{1}{7}$
Slope of the perpendicular line: $m_\perp = -\dfrac{1}{m} = -7$
The perpendicular line has x-intercept $3$, so it passes through $(3, 0)$. Using point-slope form:
$$y – 0 = -7(x – 3)$$
$$y = -7x + 21$$
Rewriting in standard form:
$$7x + y = 21$$
Hence, the equation of the perpendicular line is:
$$7x + y = 21$$
Coordinate geometry exercises by Anand Classes for IIT JEE, NDA, CUET practice with detailed slope and intercept methods.
NCERT Question.8 :
Find angles between the lines $\sqrt{3}x + y = 1$ and $x + \sqrt{3}y = 1$.
Solution:
Given lines:
$$\sqrt{3}x + y = 1 \quad \text{and} \quad x + \sqrt{3}y = 1$$
Slope-intercept forms:
$$y = -\sqrt{3}x + 1 \quad \text{(i)}$$
$$y = -\frac{1}{\sqrt{3}}x + \frac{1}{\sqrt{3}} \quad \text{(ii)}$$
Slopes: $m_1 = -\sqrt{3}$, $m_2 = -\dfrac{1}{\sqrt{3}}$
Angle between two lines:
$$\tan \theta = \left| \frac{m_1 – m_2}{1 + m_1 m_2} \right|$$
$$\tan \theta = \left| \frac{-\sqrt{3} – (-1/\sqrt{3})}{1 + (-\sqrt{3})(-1/\sqrt{3})} \right| = \frac{1}{\sqrt{3}}$$
$$\theta = 30^\circ$$
Hence, the angle between the lines is either $30^\circ$ or $180^\circ – 30^\circ = 150^\circ$.
NCERT Question.9 :
The line through the points $(h, 3)$ and $(4, 1)$ intersects the line $7x − 9y −19 = 0$ at right angle. Find the value of $h$.
Solution:
Slope of the line through $(h, 3)$ and $(4, 1)$:
$$m_1 = \frac{1 – 3}{4 – h} = \frac{-2}{4 – h}$$
Slope of the line $7x – 9y – 19 = 0$:
$$y = \frac{7}{9}x – \frac{19}{9} \quad \Rightarrow \quad m_2 = \frac{7}{9}$$
Given lines are perpendicular:
$$m_1 \cdot m_2 = -1$$
$$\frac{-2}{4 – h} \cdot \frac{7}{9} = -1$$
$$\frac{-14}{36 – 9h} = -1$$
$$36 – 9h = 14$$
$$9h = 22 \quad \Rightarrow \quad h = \frac{22}{9}$$
Hence, $h = \dfrac{22}{9}$.
NCERT Question 10.
Prove that the line through the point $(x_1, y_1)$ and parallel to the line $Ax + By + C = 0$ is $A(x – x_1) + B(y – y_1) = 0$.
Solution:
Slope of the line $Ax + By + C = 0$:
$$y = -\frac{A}{B}x – \frac{C}{B} \quad \Rightarrow \quad m = -\frac{A}{B}$$
Equation of a line passing through $(x_1, y_1)$ with slope $m$:
$$y – y_1 = m(x – x_1)$$
$$y – y_1 = -\frac{A}{B}(x – x_1)$$
Multiply both sides by $B$:
$$B(y – y_1) = -A(x – x_1)$$
$$A(x – x_1) + B(y – y_1) = 0$$
Hence proved.
Practice coordinate geometry with Anand Classes for IIT JEE, NDA, CUET, and detailed solutions of lines and slopes.
NCERT Question 11.
Two lines passing through the point $(2, 3)$ intersect each other at an angle of $60^\circ$. If slope of one line is $2$, find the equation of the other line.
Solution:
Let slope of first line be $m_1 = 2$ and slope of the other line be $m_2$.
Angle between two lines:
$$\tan \theta = \left| \frac{m_1 – m_2}{1 + m_1 m_2} \right|$$
$$\tan 60^\circ = \left| \frac{2 – m_2}{1 + 2 m_2} \right|$$
$$\sqrt{3} = \pm \frac{2 – m_2}{1 + 2 m_2}$$
Solving, we get two cases:
Case 1:
$$m_2 = \frac{2 – \sqrt{3}}{2\sqrt{3} + 1}$$
Equation of line passing through $(2, 3)$:
$$y – 3 = \frac{2 – \sqrt{3}}{2\sqrt{3} + 1}(x – 2)$$
Simplifying:
$$(\sqrt{3} – 2)x + (2\sqrt{3} + 1)y = 8\sqrt{3} – 1$$
Case 2:
$$m_2 = -\frac{2 – \sqrt{3}}{2\sqrt{3} + 1}$$
Equation of line passing through $(2, 3)$:
$$y – 3 = -\frac{2 – \sqrt{3}}{2\sqrt{3} + 1}(x – 2)$$
Simplifying:
$$(\sqrt{3} + 2)x + (2\sqrt{3} – 1)y = 8\sqrt{3} + 1$$
NCERT Question 12.
Find the equation of the right bisector of the line segment joining the points $(3, 4)$ and $(–1, 2)$.
Solution:
Midpoint of AB:
$$x = \frac{3 + (-1)}{2} = 1, \quad y = \frac{4 + 2}{2} = 3$$
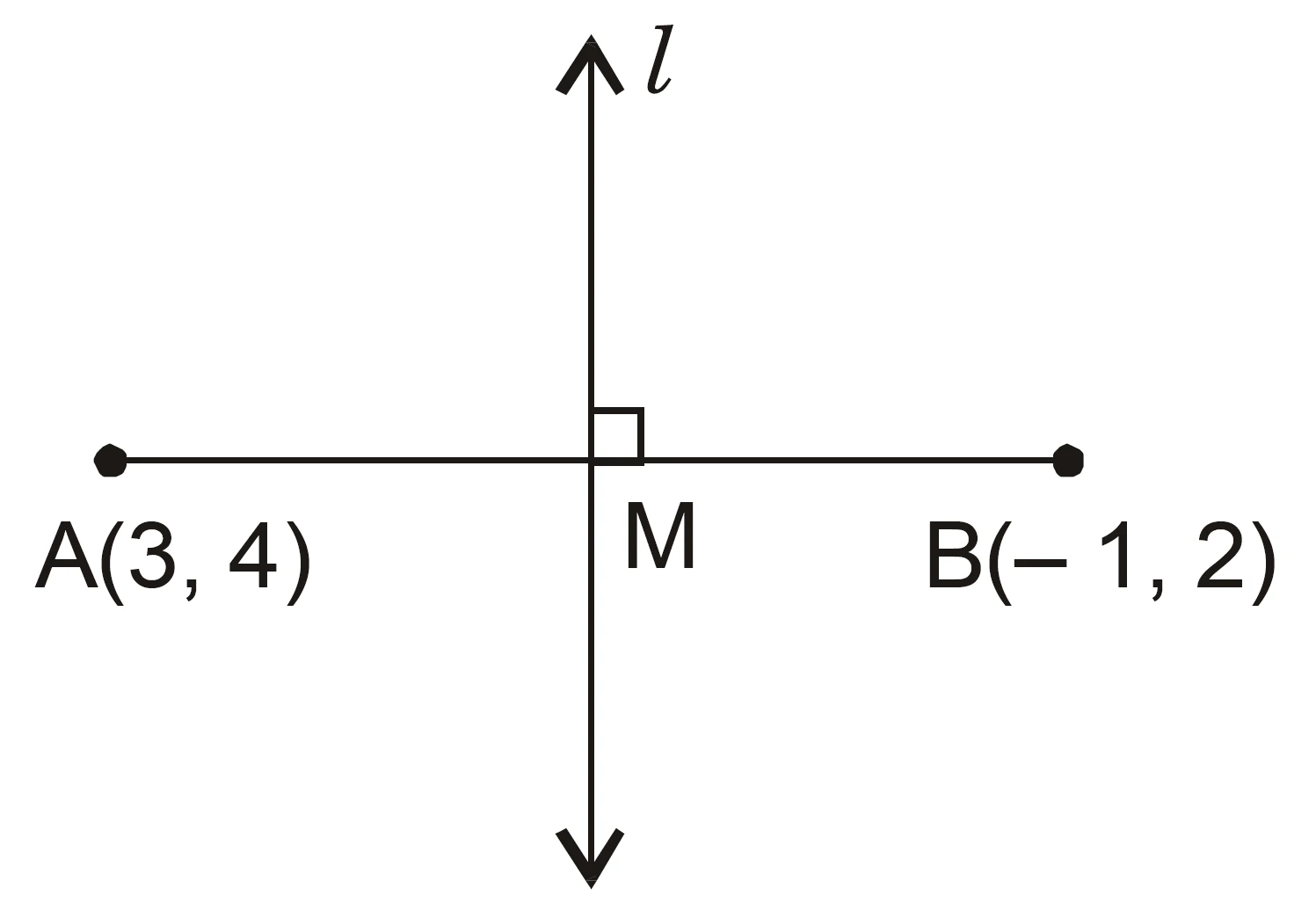
$$\text{Midpoint} = M(1, 3)$$
Slope of AB:
$$m_1 = \frac{2 – 4}{-1 – 3} = \frac{-2}{-4} = \frac{1}{2}$$
Slope of perpendicular bisector $l$ :
$$m_2 = -\frac{1}{m_1} = -2$$
Equation of line $l$ passing through midpoint $M(1, 3)$ with slope $-2$:
$$y – 3 = -2(x – 1)$$
$$y – 3 = -2x + 2$$
$$2x + y = 5$$
Hence, the equation of the right bisector is $2x + y = 5$.
For complete practice of line equations and coordinate geometry, download PDF solutions by Anand Classes, trusted for IIT JEE, NDA, CUET preparation.
NCERT Question 13.
Find the coordinates of the foot of perpendicular from the point $(-1, 3)$ to the line $3x – 4y – 16 = 0$.
Solution:
Let the foot of the perpendicular be $M(a, b)$.
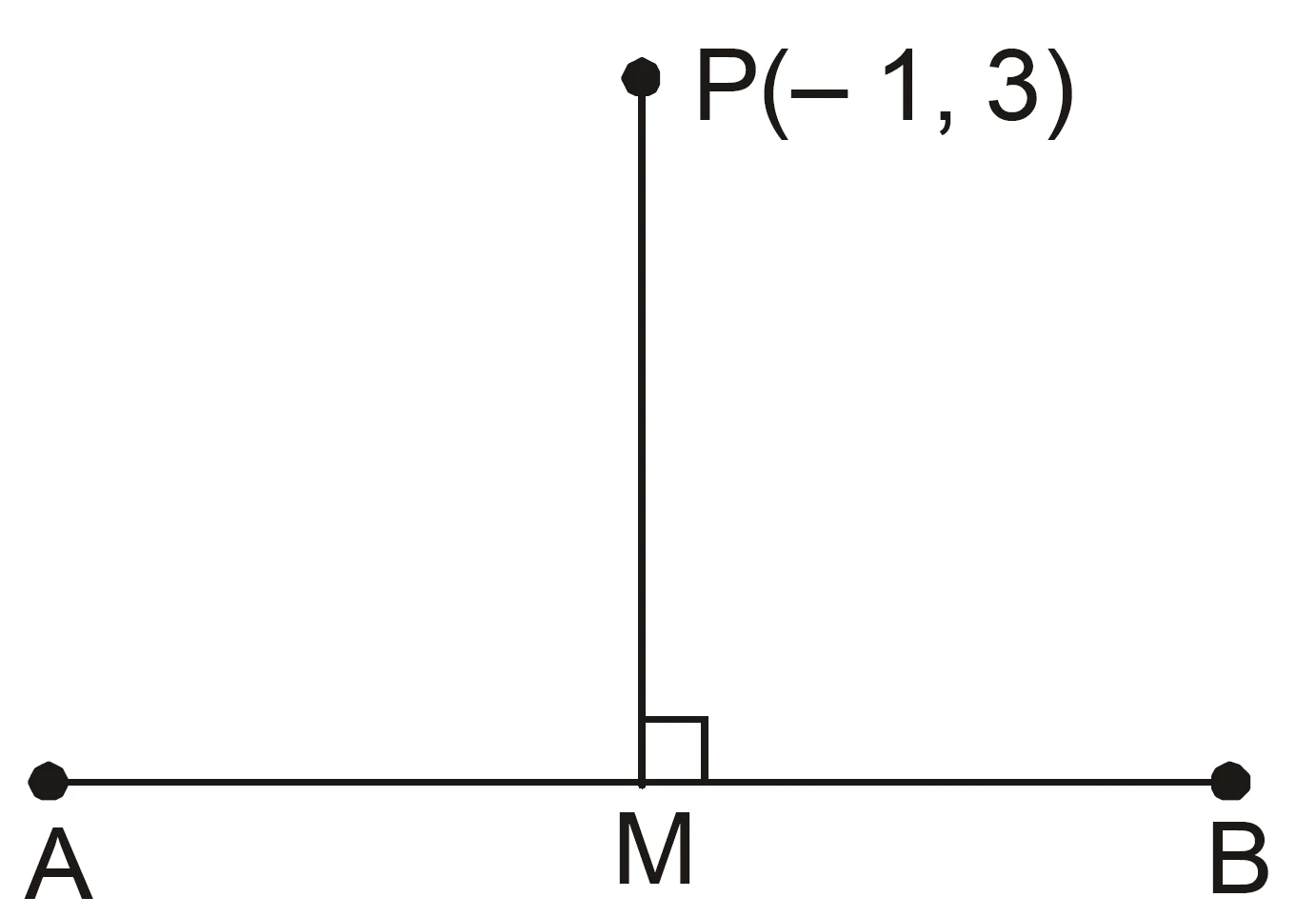
Slope of the line joining $P(-1, 3)$ and $M(a, b)$:
$$m_1 = \frac{b – 3}{a + 1}$$
Slope of the given line AB is : $3x – 4y – 16 = 0$:
$$y = \frac{3}{4}x – 4 \implies m_2 = \frac{3}{4}$$
Since the lines $PM$ and $AB$ are perpendicular:
$$m_1 \cdot m_2 = -1$$
$$\frac{b – 3}{a + 1} \cdot \frac{3}{4} = -1$$
$$3b – 9 = -4a – 4$$
$$4a + 3b = 5 \quad \text{(i)}$$
Point $(a, b)$ lies on the given line $3x – 4y – 16 = 0$ :
$$3a – 4b = 16 \quad \text{(ii)}$$
Solving (i) and (ii), we get:
$$a = \frac{68}{25}, \quad b = -\frac{49}{25}$$
Hence, the coordinates of the foot of the perpendicular are:
$$M(\dfrac{68}{25}, -\dfrac{49}{25})$$
NCERT Question 14.
The perpendicular from the origin to the line $y = mx + c$ meets it at the point $(-1, 2)$. Find the values of $m$ and $c$.
Solution:
Slope of the line joining $O(0, 0)$ and $A(-1, 2)$:
$$m_{\text{perp}} = \frac{2 – 0}{-1 – 0} = -2$$
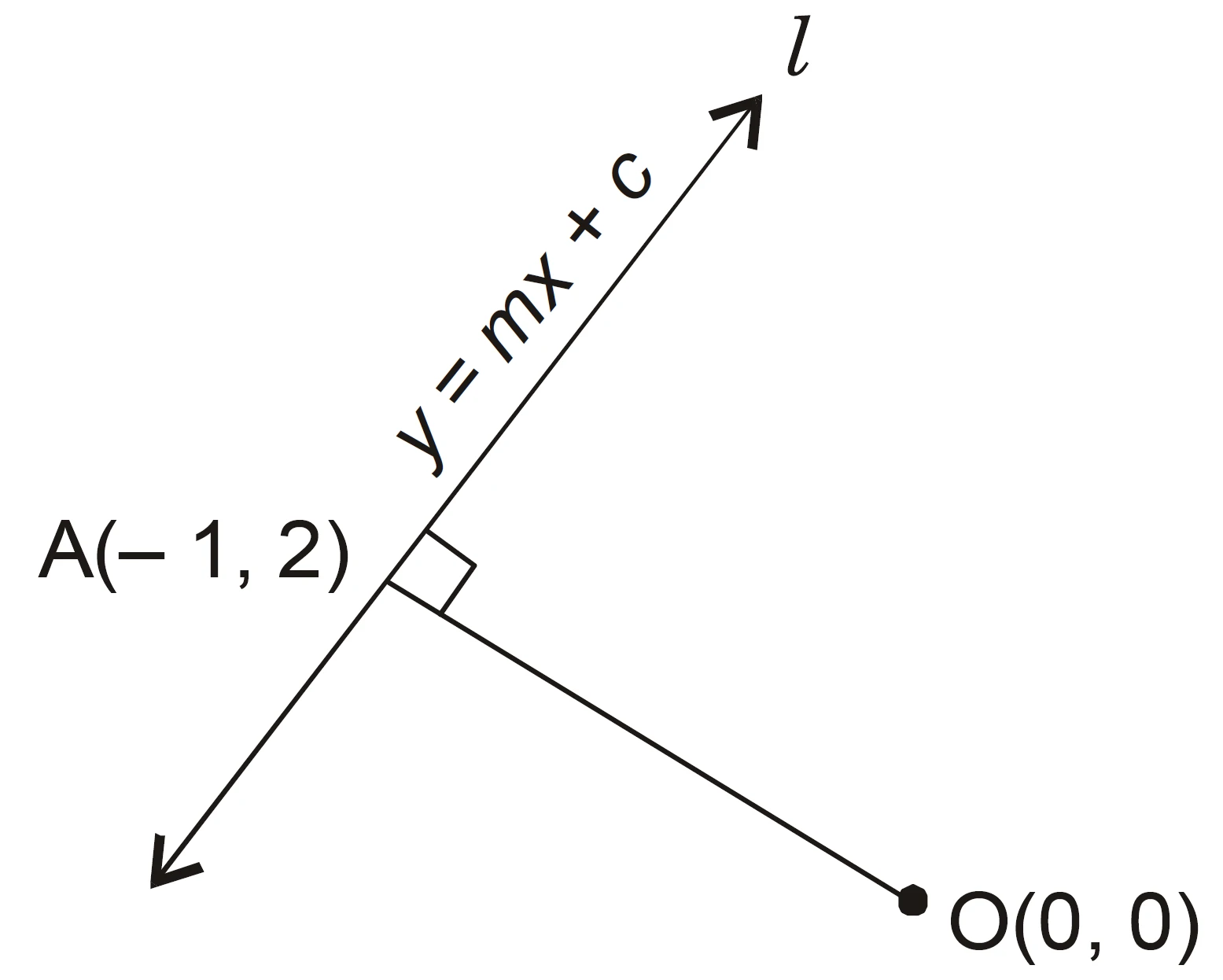
Slope of given line $y = mx + c$ is $m$. Since lines are perpendicular:
$$m \cdot (-2) = -1 \implies m = \frac{1}{2}$$
Point $(-1, 2)$ lies on the line $y = mx + c$:
$$2 = \frac{1}{2}(-1) + c \implies c = \frac{5}{2}$$
Hence,
$$m = \frac{1}{2}, \quad c = \frac{5}{2}$$
For more solved problems in coordinate geometry and line equations, Anand Classes provides comprehensive solutions for IIT JEE, NDA, and CUET preparation.
NCERT Question 15 :
If $p$ and $q$ are the lengths of perpendiculars from the origin to the lines $$
x\cos\theta – y\sin\theta = k\cos 2\theta
\qquad\text{and}\qquad
x\sec\theta + y\csc\theta = k,
$$ respectively, prove that $p^2 + 4q^2 = k^2$.
Solution :
For a line $Ax+By+C=0$, the perpendicular distance from the origin is
$$
d=\frac{|C|}{\sqrt{A^2+B^2}}.
$$
For the first line $x\cos\theta – y\sin\theta = k\cos 2\theta$, write it as
$$
\cos\theta \;x -\sin\theta \;y -\; k\cos2\theta = 0.
$$
Thus $A=\cos\theta$ , $B=-\sin\theta$ , $C=-k\cos2\theta$. Hence
$$
p=\frac{|C|}{\sqrt{A^2+B^2}}=\frac{|k\cos2\theta|}{\sqrt{\cos^2\theta+\sin^2\theta}}
=|k\cos2\theta|.
$$
Squaring,
$$
p^2=k^2\cos^2 2\theta. \tag{1}
$$
For the second line $x\sec\theta + y\csc\theta = k$, write
$$
\sec\theta \;x + \csc\theta \;y \;- k = 0.
$$
So $A=\sec\theta, B=\csc\theta, C=-k$. Thus
$$
q=\frac{|C|}{\sqrt{A^2+B^2}}=\frac{k}{\sqrt{\sec^2\theta+\csc^2\theta}}.
$$
Compute the denominator:
$$
\sec^2\theta+\csc^2\theta=\frac{1}{\cos^2\theta}+\frac{1}{\sin^2\theta}
=\frac{\sin^2\theta+\cos^2\theta}{\sin^2\theta\cos^2\theta}
=\frac{1}{\sin^2\theta\cos^2\theta}.
$$
Hence
$$
q=\frac{k}{1/(|\sin\theta\cos\theta|)}=k|\sin\theta\cos\theta|.
$$
Therefore
$$
4q^2=4k^2\sin^2\theta\cos^2\theta = k^2\sin^2 2\theta. \tag{2}
$$
Adding (1) and (2):
$$
p^2+4q^2=k^2\big(\cos^2 2\theta+\sin^2 2\theta\big)=k^2.
$$
Hence $p^2+4q^2=k^2$.
(Prepared from Anand Classes’ coordinate-geometry notes — useful for JEE/CUET practice.)
NCERT Question 16 :
In $\triangle ABC$ with $A(2,3), B(4,-1), C(1,2)$, find the equation and length of the altitude from vertex $A$.
Solution :
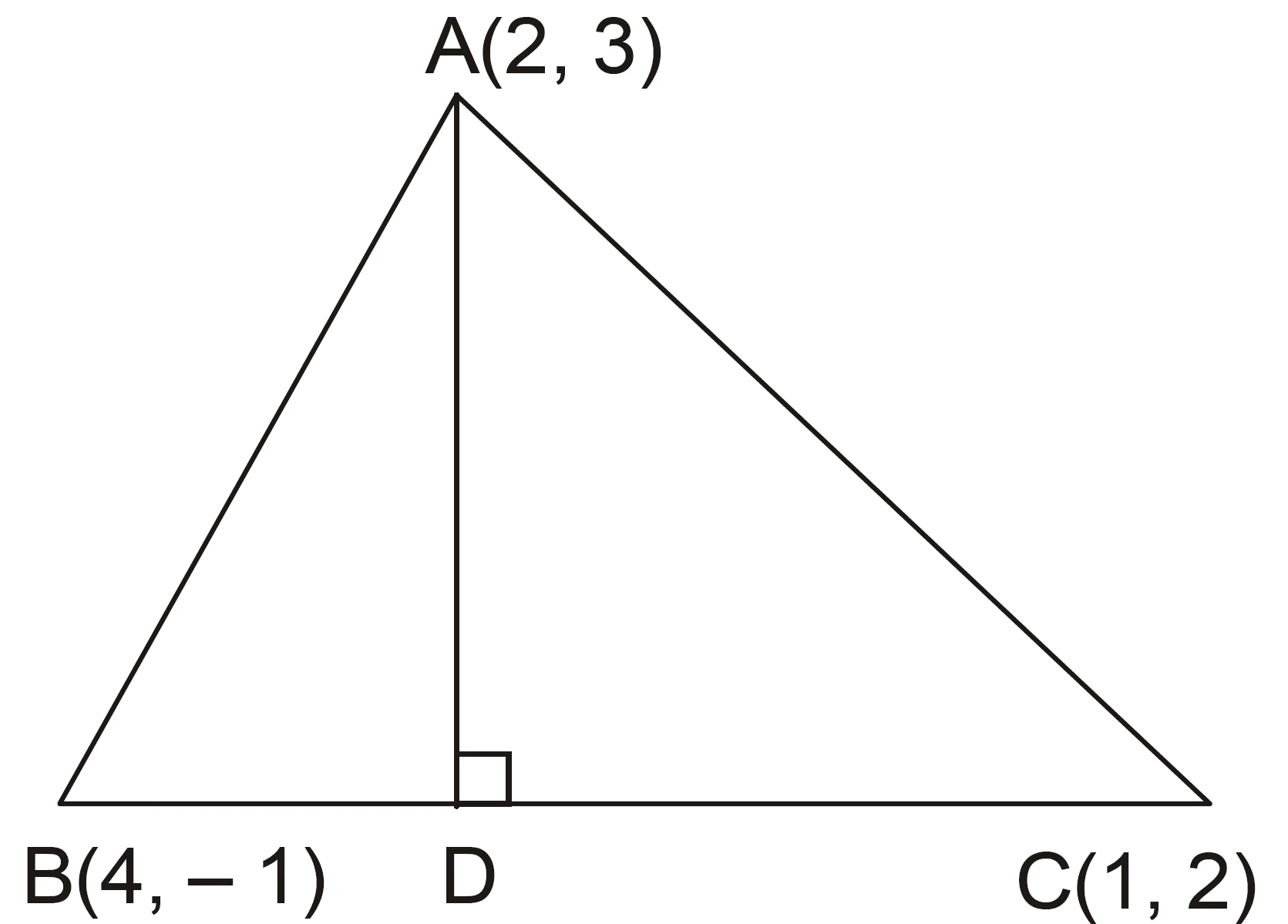
Slope of $BC$:
$$
m_{BC}=\frac{-1-2}{4-1}=\frac{-3}{3}=-1.
$$
Slope of altitude $AD$ from $A$ (perpendicular to $BC$) is
$$
m_{AD}=-\frac{1}{m_{BC}}=1.
$$
Equation of the altitude $AD$ through $A(2,3)$:
$$
y-3=1(x-2)\quad\Longrightarrow\quad y-x=1.
$$
To find its length, compute distance from $A$ to line $BC$.
Equation of $BC$ :
using two-point form from $B(4,-1)$ and slope $-1$,
$$
y+1=-1(x-4)\quad\Longrightarrow\quad x+y-3=0.
$$
Distance from $A(2,3)$ to line $BC$ : $x+y-3=0$:
$$
\text{AD}=\frac{|1\cdot2+1\cdot3-3|}{\sqrt{1^2+1^2}}
=\frac{|2+3-3|}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}.
$$
Equation of altitude: $y-x=1$.
Length of altitude: $\sqrt{2}$ units.
(Worked example from Anand Classes — altitude and distance formula practice for competitive exams.)
NCERT Question 17.
If $p$ is the length of the perpendicular from the origin to the line whose intercepts on the axes are $a$ and $b$, then show that
$$\dfrac{1}{p^2} = \dfrac{1}{a^2} + \dfrac{1}{b^2}$$
Solution:
Equation of a line whose intercepts on the axes are $a$ and $b$ is
$$\dfrac{x}{a} + \dfrac{y}{b} = 1$$
Multiplying through by $ab$, we get
$$bx + ay = ab$$
or
$$bx + ay – ab = 0 \quad \text{…(i)}$$
The perpendicular distance $d$ of a line $Ax + By + C = 0$ from a point $(x_1, y_1)$ is given by
$$d = \dfrac{|Ax_1 + By_1 + C|}{\sqrt{A^2 + B^2}}$$
Comparing equation (i) with $Ax + By + C = 0$, we get
$$A = b, \quad B = a, \quad C = -ab$$
Let $p$ be the length of the perpendicular from $(0, 0)$ to the line (i), then
$$p = \dfrac{|A(0) + B(0) + C|}{\sqrt{A^2 + B^2}} = \dfrac{|-ab|}{\sqrt{a^2 + b^2}} = \dfrac{ab}{\sqrt{a^2 + b^2}}$$
Now, squaring both sides:
$$p^2 = \dfrac{a^2 b^2}{a^2 + b^2}$$
Taking the reciprocal,
$$\dfrac{1}{p^2} = \dfrac{a^2 + b^2}{a^2 b^2} = \dfrac{1}{a^2} + \frac{1}{b^2}$$
Hence,
$$\boxed{\dfrac{1}{p^2} = \dfrac{1}{a^2} + \dfrac{1}{b^2}}$$
This completes the proof.
Explore more coordinate geometry solutions and NCERT problems with Anand Classes, a trusted name for IIT JEE, NDA, and CUET preparation.


