NCERT Solutions Straight Lines Exercise 9.2 (2025-2026) | Free PDF Download

Anand Classes provides NCERT Solutions for Class 11 Maths Chapter 9 – Straight Lines (Exercise 9.2) for the 2025–2026 session, prepared according to the latest CBSE and NCERT syllabus. This exercise focuses on the equations of straight lines in different forms such as the slope-intercept form, point-slope form, two-point form, and intercept form. The solutions are explained step-by-step with proper reasoning, helping students master the concepts of coordinate geometry essential for CBSE exams, JEE Main, JEE Advanced, NDA, and CUET. Each question is solved systematically to ensure conceptual clarity and accuracy. Click the print button to download study material and notes in PDF format.

---

NCERT Question.1 : Write the equations of lines for the x- and y-axes.

Solution:
The y-coordinate of every point on the x-axis is $0$, and the x-coordinate of every point on the y-axis is $0$. So,
Equation of x-axis:
$$
y = 0
$$
Equation of y-axis:
$$
x = 0
$$

These basic coordinate geometry concepts are part of NCERT Solutions by Anand Classes, the best coaching institute for IIT JEE, NDA, and CUET exams.

---

NCERT Question.2 : Find the equation of the line which passing through the point (–4, 3) with slope $\frac{1}{2}$.

Solution:
Given that the point $P(x_1, y_1)$ is $(-4, 3)$ and the slope $m = \frac{1}{2}$.
Equation of the line is given by:
$$
y – y_1 = m(x – x_1)
$$
Substituting the values,
$$
y – 3 = \frac{1}{2}(x + 4)
$$

$$
2(y – 3) = x + 4
$$

$$
x – 2y + 10 = 0
$$

So, the equation of the line is
$$
x – 2y + 10 = 0
$$

Concepts of slope and line equation are important for Class 11 and 12 NCERT coordinate geometry, and are well explained in Anand Classes’ IIT JEE and NDA coaching notes.

---

NCERT Question.3 : Find the equation of the line which passing through (0, 0) with slope m.

Solution:
Given that the point $P(x_1, y_1)$ is $(0, 0)$ and the slope is $m$.
Equation of the line:
$$
y – y_1 = m(x – x_1)
$$

Substituting values,
$$
y = mx
$$
or
$$
y – mx = 0
$$

This simple equation represents all straight lines passing through the origin, and is a key concept in NCERT Class 11 Coordinate Geometry, prepared by Anand Classes, the top institute for IIT JEE and CUET exam preparation.

---

Question.4 : Find the equation of the line which passing through (2, 2√3) and inclined with the x-axis at an angle of 75°.

Solution:
Given that $P(x_1, y_1) = (2, 2\sqrt{3})$ and angle $\theta = 75°$.

Equation of the line:
$$
y – y_1 = m(x – x_1)
$$
where $m = \tan \theta$
Now,
$$
m = \tan 75°
$$
Using the identity $\tan(A + B) = \dfrac{\tan A + \tan B}{1 – \tan A \tan B}$
$$
\tan 75° = \tan(45° + 30°)
$$

$$
\tan 75° = \frac{1 + \dfrac{1}{\sqrt{3}}}{1 – \dfrac{1}{\sqrt{3}}}
$$
Rationalizing,
$$
\tan 75° = 2 + \sqrt{3}
$$

Substituting in the line equation,
$$
(y – 2\sqrt{3}) = (2 + \sqrt{3})(x – 2)
$$
Expanding,
$$
(2 + \sqrt{3})x – y – 4 = 0
$$

Hence, the equation of the required line is
$$
(2 + \sqrt{3})x – y – 4 = 0
$$

This question is from NCERT Class 11 Coordinate Geometry Chapter – Straight Lines, fully solved and explained by Anand Classes, providing step-by-step JEE and NDA preparation notes.

---

NCERT Question.5 : Find the equation of the line which Intersecting the x-axis at a distance of 3 units to the left of origin with slope –2.

Solution:
Given that slope $m = -2$ and x-intercept $= 3$,
that means the line passes through point $P(x_1, y_1) = (-3, 0)$ (since it is to the left of origin).

Equation of the line is
$$
y – y_1 = m(x – x_1)
$$

Substitute values:
$$
y – 0 = (-2)(x – (-3))
$$

$$
y = -2(x + 3)
$$

$$
y = -2x – 6
$$
Rewriting in standard form:
$$
2x + y + 6 = 0
$$

Hence, the equation of the line is
$$
2x + y + 6 = 0
$$

This example helps understand the concept of x-intercept and slope form of a line, commonly covered in NCERT Class 11 Coordinate Geometry and detailed in Anand Classes IIT JEE and NDA handwritten notes.

---

NCERT Question.6 : Find the equation of the straight line which Intersecting the y-axis at a distance of 2 units above the origin and making an angle of 30° with the positive direction of the x-axis.

Solution:
Given:
Angle $\theta = 30°$
Slope, $m = \tan 30° = \dfrac{1}{\sqrt{3}}$
Point on y-axis: $(0, 2)$
Equation of the line:
$$
y – y_1 = m(x – x_1)
$$
Substituting:
$$
y – 2 = \frac{1}{\sqrt{3}}(x-0)
$$

$$
\sqrt{3}y – 2\sqrt{3} = x
$$
Rewriting,
$$
x – \sqrt{3}y + 2\sqrt{3} = 0
$$
Hence, the required equation of the line is
$$
x – \sqrt{3}y + 2\sqrt{3} = 0
$$

This topic of lines inclined at an angle with axes is part of Class 11 NCERT Coordinate Geometry and is clearly explained in Anand Classes’ JEE, CUET, and NDA preparation materials.

---

NCERT Question.7 : Find the equation of the straight line which passing through the points (–1, 1) and (2, –4).

Solution:
Given points:
$P_1(x_1, y_1) = (-1, 1)$ and $P_2(x_2, y_2) = (2, -4)$
Slope of the line:
$$
m = \frac{y_2 – y_1}{x_2 – x_1} = \frac{-4 – 1}{2 – (-1)} = \frac{-5}{3}
$$
Equation of the line:
$$
y – y_1 = m(x – x_1)
$$
Substituting,
$$
y – 1 = \frac{-5}{3}(x + 1)
$$
Multiplying both sides by 3:
$$
3y – 3 = -5x – 5
$$

$$
5x + 3y + 2 = 0
$$
Hence, the equation of the line is
$$
5x + 3y + 2 = 0
$$

This question involves using the two-point form of the equation of a line, an essential part of NCERT Class 11 Chapter – Straight Lines, well-covered in Anand Classes’ IIT JEE and NDA maths notes.

---

NCERT Question.8 : The vertices of $\triangle PQR$ are $P(2,1),\ Q(-2,3),\ R(4,5)$. Find the equation of the median through the vertex $R$.

Solution :
Midpoint $M$ of $PQ$:
$$
M=\Big(\frac{2+(-2)}{2},\frac{1+3}{2}\Big)=(0,2).
$$

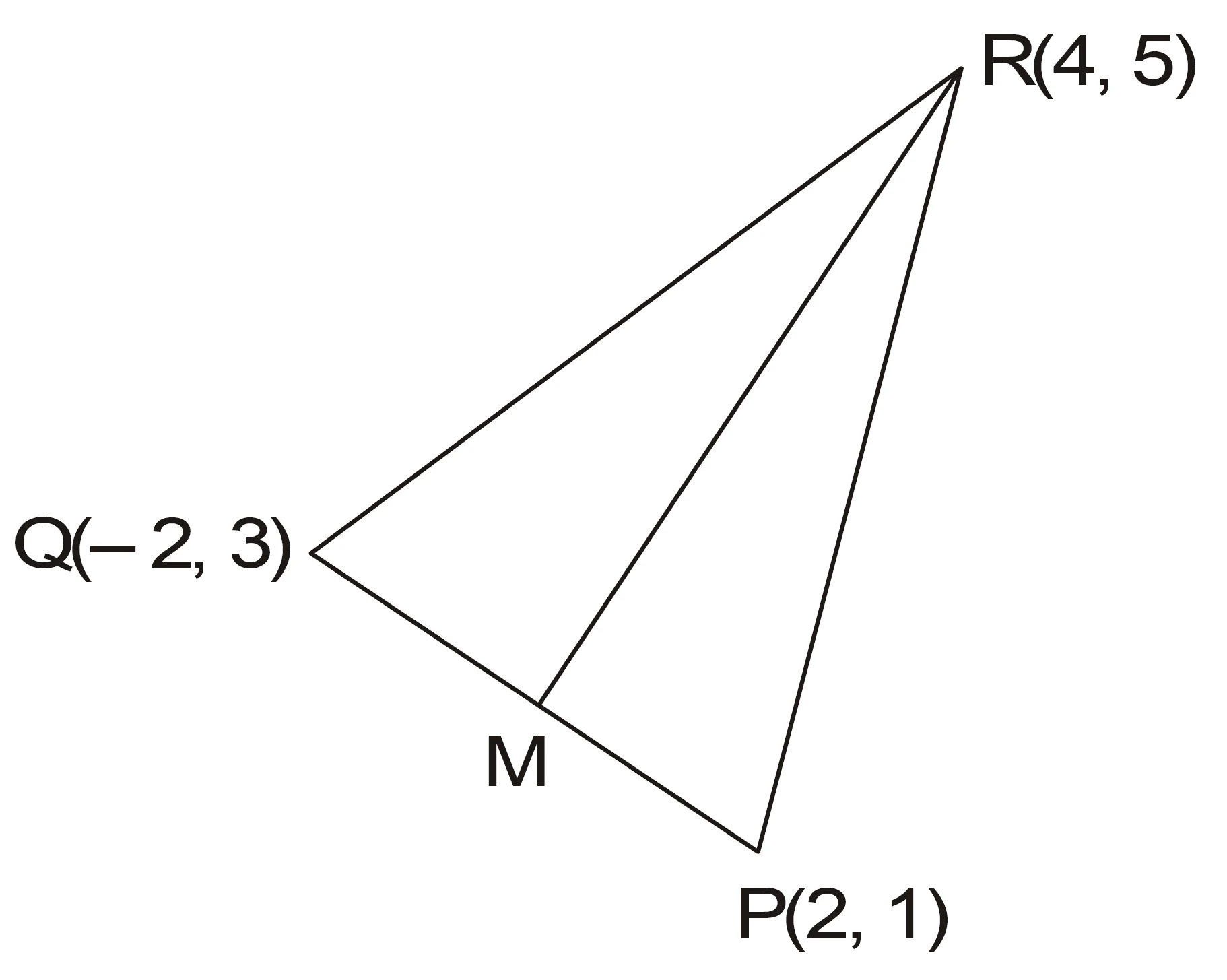
Slope of line $RM$:
$$
m_{RM}=\frac{2-5}{0-4}=\frac{-3}{-4}=\frac{3}{4}.
$$
Equation of line $RM$ (Point–slope form) through $R(4,5)$:
$$
y-5=\frac{3}{4}(x-4).
$$
Multiply by $4$ and simplify:
$$
4(y-5)=3(x-4)
$$

$$
4y-20=3x-12
$$

$$
3x-4y+8=0.
$$

Answer: $;3x-4y+8=0.$

Download the worked NCERT solution on medians and midpoints by Anand Classes — useful for JEE/CUET practice.

---

NCERT Question.9 : Find the equation of the line passing through $(-3,5)$ and perpendicular to the line through $(2,5)$ and $(-3,6)$.

Solution :
Slope of the line l₁ through $(2,5)$ and $(-3,6)$:
$$
m_1=\frac{6-5}{-3-2}=\frac{1}{-5}=-\dfrac{1}{5}.
$$

Slope of the required perpendicular line l₂
$$
m=-\frac{1}{m_1}= -\frac{1}{-1/5}=5.
$$

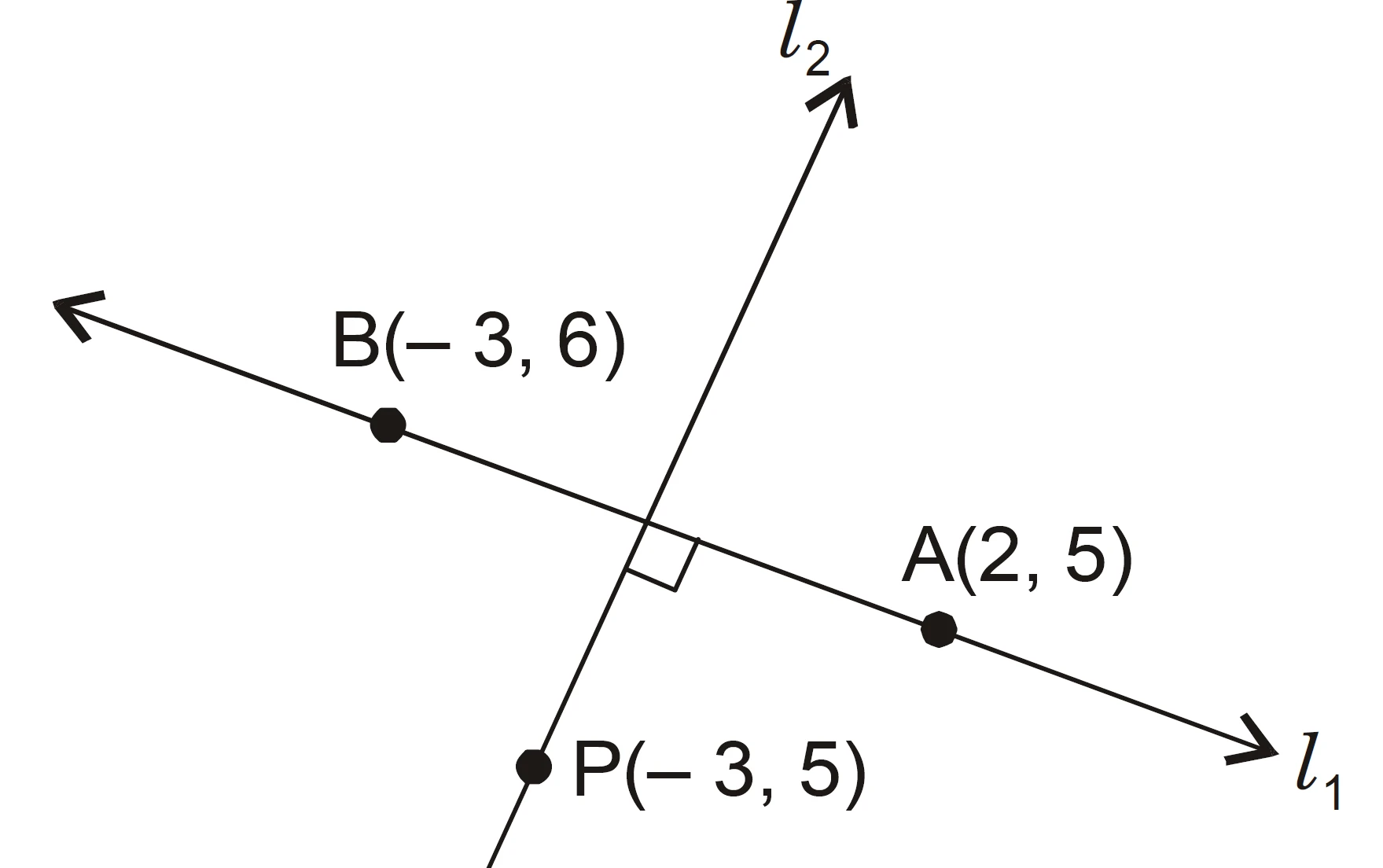
Line l₂ through $(-3,5)$ with slope $5$:
$$
y-5=5\big(x-(-3)\big)
$$

$$
y-5=5x+15
$$

$$
5x-y+20=0.
$$

Answer: $5x-y+20=0$

Grab the perpendicular-lines worksheet PDF from Anand Classes — great for NDA and JEE revision.

---

NCERT Question.10 : A line perpendicular to the line segment joining $(1,0)$ and $(2,3)$ divides it internally in the ratio $1:n$. Find the equation of that line.

Solution :
Slope of segment from $(1,0)$ to $(2,3)$:
$$
m_1=\frac{3-0}{2-1}=3.
$$
Slope of required perpendicular line:
$$
m_2=-\frac{1}{3}.
$$

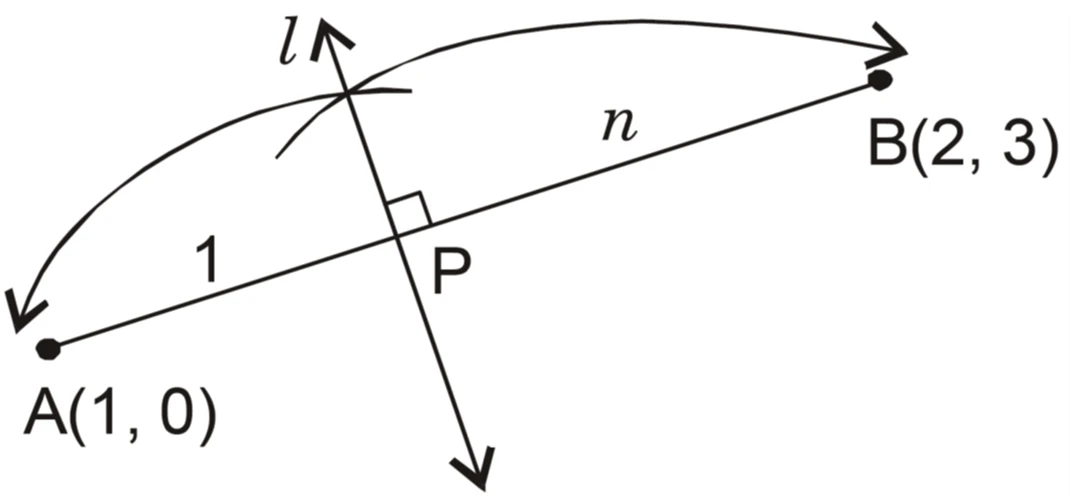
Point $P(a, b)$ dividing $A(1,0)$ and $B(2,3)$ in ratio $1:n$ (internal):
$$
a=\frac{1\cdot 2 + n\cdot 1}{1+n}=\frac{2+n}{1+n}
$$

$$
b=\frac{1\cdot 3 + n\cdot 0}{1+n}=\frac{3}{1+n}.
$$

Equation of line through $P(a,b)$ with slope $m_2$:
$$
y-\frac{3}{1+n}=-\frac{1}{3}\Big(x-\frac{2+n}{1+n}\Big).
$$
Multiply both sides by $3(1+n)$ and simplify:
$$
3(1+n)y-9=-(1+n)x+(2+n)
$$

$$
(1+n)x+3(1+n)y-(n+11)=0.
$$

Answer: $(1+n)x+3(1+n)y-(n+11)=0.$

Download the step-by-step NCERT solutions PDF on section formula and perpendiculars by Anand Classes — ideal for JEE/CUET practice.

---

NCERT Question.11 : Find the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the point $(2, 3)$.

Solution
Let the intercepts on the x-axis and y-axis be $a$ and $b$, respectively.
Given that the line cuts off equal intercepts,
$$
a = b
$$

Equation of a line with intercepts $a$ and $b$ is

$$
\frac{x}{a} + \frac{y}{b} = 1
$$
Substituting $a = b$, we get
$$
\frac{x}{a} + \frac{y}{a} = 1
$$

$$
x + y = a \quad \text{…(1)}
$$

The line passes through $(2, 3)$, so
$$
2 + 3 = a \Rightarrow a = 5
$$
Substituting in equation (1):
$$
x + y = 5
$$

$$
x + y – 5 = 0
$$

Answer: $ x + y – 5 = 0.$

Download detailed NCERT Class 11 coordinate geometry solutions PDF by Anand Classes — ideal for IIT JEE and CUET aspirants.

---

NCERT Question.12 : Find the equation of the line passing through the point $(2, 2)$ and cutting off intercepts on the axes whose sum is $9$.

Solution
Equation of the line making intercepts $a$ and $b$ on x-axis and y-axis respectively is
$$
\frac{x}{a} + \frac{y}{b} = 1 \quad \text{…(1)}
$$
Given that
$$
a + b = 9 \quad \Rightarrow \quad b = 9 – a
$$
Substituting in (1):
$$
\frac{x}{a} + \frac{y}{9 – a} = 1
$$
The line passes through $(2, 2)$, hence

$$
\frac{2}{a} + \frac{2}{9 – a} = 1
$$
Simplify:
$$
\frac{2(9 – a) + 2a}{a(9 – a)} = 1
$$

$$
\frac{18}{a(9 – a)} = 1
$$

$$
18 = a(9 – a)
$$

$$
a^2 – 9a + 18 = 0
$$
Factorizing:

$$
a^2 – 3a – 6a + 18 = 0
$$

$$
a(a – 3) – 6(a – 3) = 0
$$

$$
(a – 3)(a – 6) = 0
$$
So, $a = 3$ or $a = 6$.

Case 1: $a = 3 \Rightarrow b = 9 – 3 = 6$
Substitute in (1):
$$
\frac{x}{3} + \frac{y}{6} = 1
$$

$$
2x + y = 6
$$

$$
2x + y – 6 = 0
$$
Case 2: $a = 6 \Rightarrow b = 9 – 6 = 3$
Substitute in (1):

$$
\frac{x}{6} + \frac{y}{3} = 1
$$

$$
x + 2y = 6
$$

$$
x + 2y – 6 = 0
$$

Answer: $ 2x + y – 6 = 0$ or $ x + 2y – 6 = 0.$

Practice more coordinate geometry exercises and download NCERT solutions PDFs by Anand Classes — best coaching for JEE, NDA, and CUET preparation.

---

NCERT Question.13 : Find equation of the line through $(0,2)$ making an angle $2\pi/3$ with the positive $x$-axis. Also find the equation of the line parallel to it and crossing the $y$-axis $2$ units below the origin.

Solution
Slope $m=\tan\big(2\pi/3\big)=\tan 120^\circ=-\sqrt{3}$.
Equation of Line through $(0,2)$ and slope =$-\sqrt{3}$ :
$$
y-2=-\sqrt{3}(x-0)
$$

$$
y-2=-\sqrt{3}x
$$

$$
\sqrt{3}x+y-2=0.
$$
Parallel line crossing $y$-axis $2$ units below origin $\Rightarrow$ point $(0,-2)$, same slope $-\sqrt{3}$ i.e equation of line passes through $(0, -2) $ and having slope = $-\sqrt{3}$ :
$$
y -(-2) =-\sqrt{3}(x-0)
$$

$$
y+2=-\sqrt{3}x
$$

$$
\sqrt{3}x+y+2=0.
$$

Answers: $\sqrt{3}x+y-2=0$ and $\sqrt{3}x+y+2=0$

Download NCERT coordinate geometry notes by Anand Classes — clear worked examples for JEE/CUET preparation.

---

NCERT Question.14 : The perpendicular from the origin to a line meets it at $(-2,9)$. Find the equation of the line.

Solution
Slope of the perpendicular (the line through origin and $A(-2,9)$):
$$
m_1=\frac{9-0}{-2-0}=-\frac{9}{2}.
$$

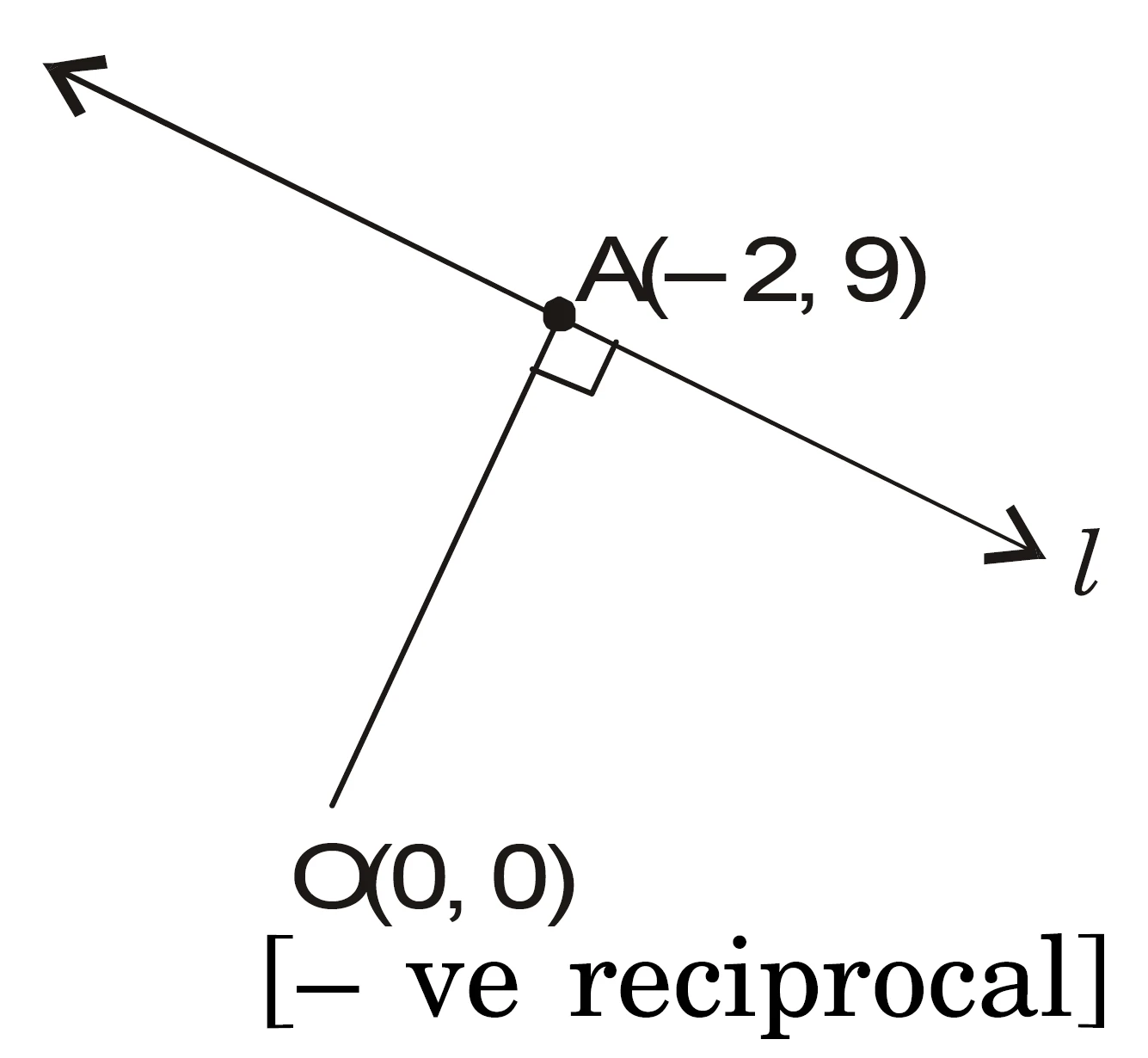
Slope $m$ of the required line is the negative reciprocal:
$$
m=-\frac{1}{m_1}=\frac{2}{9}.
$$
Line through $(-2,9)$ with slope $2/9$:
$$
y-9=\frac{2}{9}\big(x+2\big)
$$
Multiply by $9$:

$$
9(y-9)=2(x+2)
$$

$$
9y-81=2x+4
$$

$$
2x-9y+85=0.
$$

Answer: $;2x-9y+85=0.$

Get the worked solution PDF on perpendiculars and slopes from Anand Classes — handy for NDA and JEE revision.

---

NCERT Question.15 : The length $L$ (in cm) of a copper rod is a linear function of its Celsius temperature $C$. In an experiment, $L = 124.942$ when $C = 20$ and $L = 125.134$ when $C = 110$. Express $L$ in terms of $C$.

Solution :
Let $L$ be taken along the $x$-axis and $C$ along the $y$-axis.
We have two points $(124.942, 20)$ and $(125.134, 110)$ in the $XY$-plane.
The equation of a line through $(x_1, y_1)$ and $(x_2, y_2)$ is:
$$
y – y_1 = \frac{(y_2 – y_1)}{(x_2 – x_1)}(x – x_1)
$$

Substituting:
$$
C – 20 = \frac{(110 – 20)}{(125.134 – 124.942)}(L – 124.942)
$$

$$
C – 20 = \frac{90}{0.192}(L – 124.942)
$$

$$
0.192(C – 20) = 90(L – 124.942)
$$

Hence,
$$
L = \frac{0.192(C – 20)}{90} + 124.942
$$

Answer:
$\displaystyle L = 124.942 + \frac{0.192}{90}(C – 20)$

Concept of linear variation applied — ideal for physics-based linear relation problems from Anand Classes notes for CUET, NDA, and JEE Mains.

---

NCERT Question.16 : The owner of a milk store finds that he can sell 980 liters of milk each week at Rs. 14/liter and 1220 liters each week at Rs. 16/liter. Assuming a linear relationship between selling price and demand, how many liters could he sell weekly at Rs. 17/liter?

Solution :
Let the selling price per liter be on the $x$-axis and demand (in liters) on the $y$-axis.
We have two points $(14, 980)$ and $(16, 1220)$.
Equation of the line:
$$
y – y_1 = \frac{(y_2 – y_1)}{(x_2 – x_1)}(x – x_1)
$$

Substitute:
$$
y – 980 = \frac{(1220 – 980)}{(16 – 14)}(x – 14)
$$

$$
y – 980 = 120(x – 14)
$$

$$
y = 120(x – 14) + 980
$$

When $x = 17$,
$$
y = 120(17 – 14) + 980
$$

$$
y = 120(3) + 980 = 1340
$$

Answer:
The owner can sell 1340 liters weekly at Rs. 17 per liter.

Practical linear demand–price relation problem — from Anand Classes applied maths series, useful for Class 11 CBSE, NDA, and JEE preparation.

---

NCERT Question.17 : $P(a,b)$ is the midpoint of a line segment between the axes. Show that the equation of the line is
$$\frac{x}{a}+\frac{y}{b}=2.$$

Solution
Let the two intercepts be $A(p,0)$ and $B(0,q)$. Midpoint of $AB$ is
$$P=\Big(\frac{p+0}{2},\frac{0+q}{2}\Big)=(\dfrac{p}{2},\dfrac{q}{2})$$

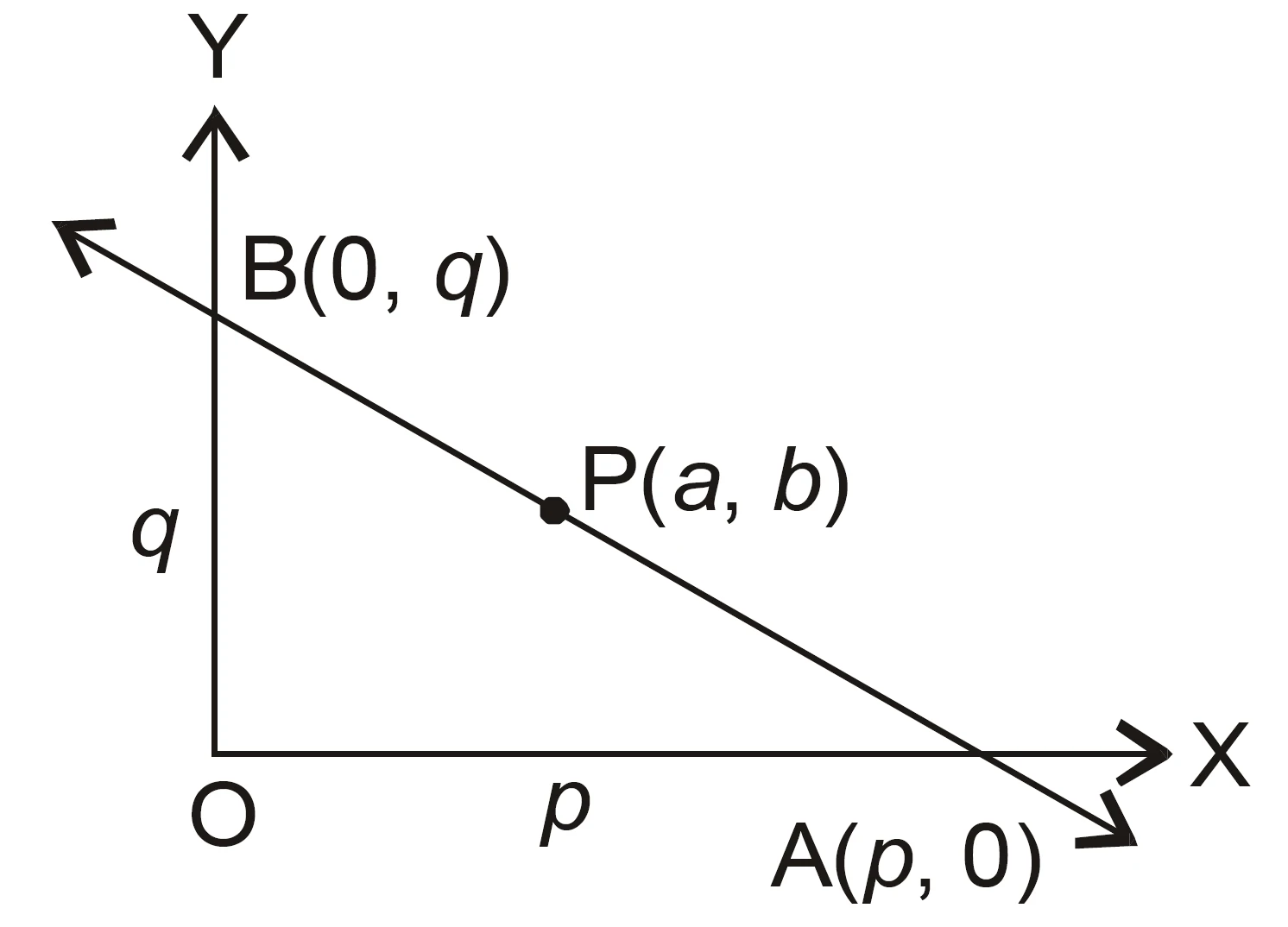
Since $P=(a,b)$, we have
$$a=\dfrac{p}{2}\implies p=2a,\qquad b=\dfrac{q}{2}\implies q=2b.$$
Thus the line passes through $(2a,0)$ and $(0,2b)$; its intercept form is
$$\frac{x}{2a}+\frac{y}{2b}=1.$$
Multiply both sides by $2$ to get
$$\frac{x}{a}+\frac{y}{b}=2.$$

(Worked example from Anand Classes — midpoint & intercepts practice for coordinate geometry.)

---

NCERT Question.18 : Point $R(h,k)$ divides a line segment between the axes in the ratio $1:2$ (internally). Find the equation of the line.

Solution
Let the equation of the line in intercept form be
$$\dfrac{x}{a} + \dfrac{y}{b} = 1 \quad \text{…(i)}$$
If it meets the x-axis at point A and y-axis at point B, then the coordinates of
$$A = (a, 0) \quad \text{and} \quad B = (0, b)$$

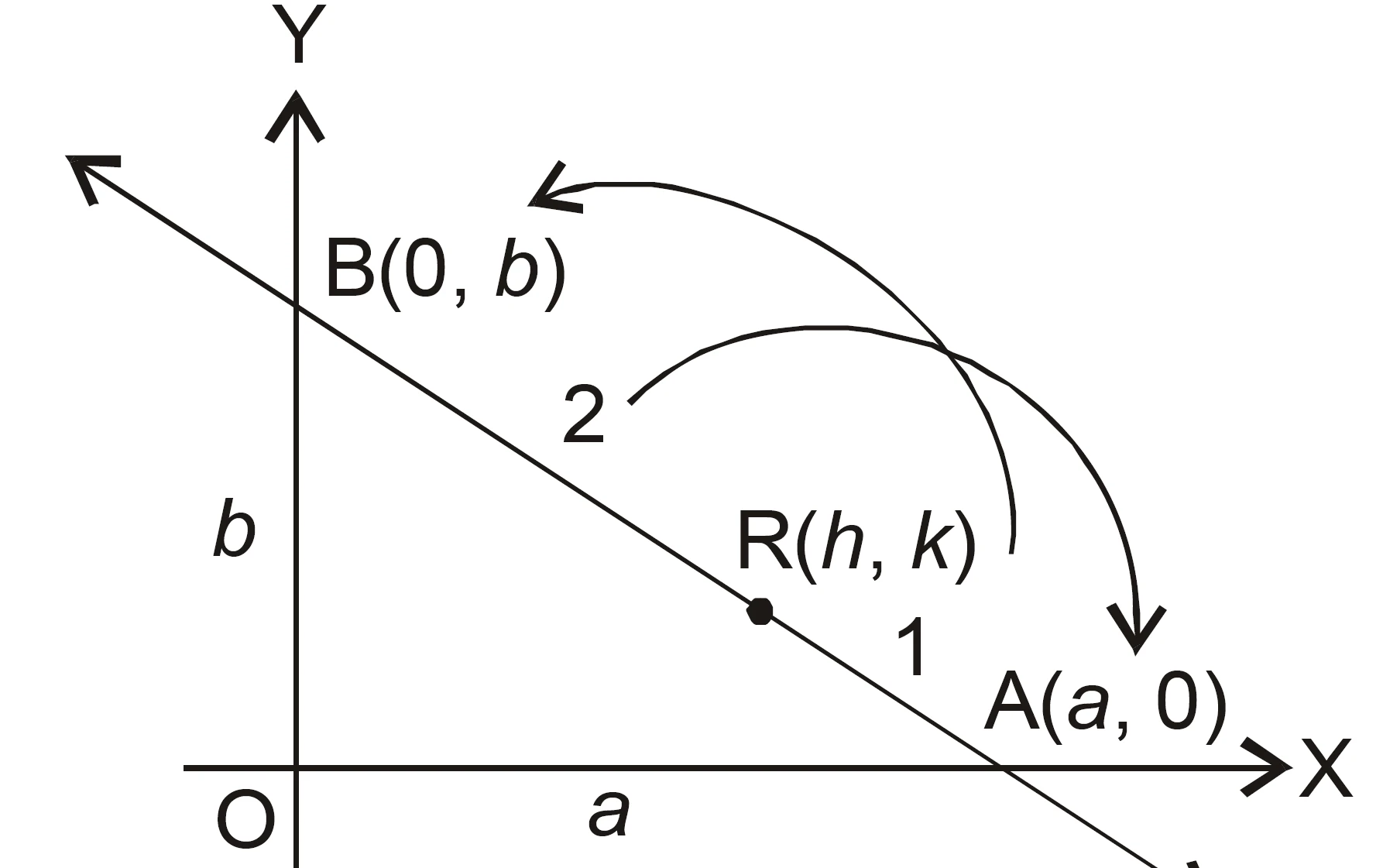
Since R(h, k) divides AB in the ratio 1 : 2, we use the section formula:
$$
R(h, k) = \left( \frac{1 \times 0 + 2 \times a}{1 + 2}, \frac{1 \times b + 2 \times 0}{1 + 2} \right)
$$
Simplifying,
$$
R(h, k) = \left( \frac{2a}{3}, \frac{b}{3} \right)
$$
Hence,
$$
h = \frac{2a}{3} \quad \text{and} \quad k = \frac{b}{3}
$$
From these, we get
$$
a = \frac{3h}{2} \quad \text{and} \quad b = 3k
$$
Substituting the values of a and b in equation (i):
$$
\frac{x}{\dfrac{3h}{2}} + \dfrac{y}{3k} = 1
$$
Simplify:
$$
\frac{2x}{3h} + \frac{y}{3k} = 1
$$
Multiply through by 3hk:
$$
2kx + hy = 3hk
$$

✅ Required equation of the line:

$$
\boxed{2kx + hy = 3hk}
$$

(Section–formula application from Anand Classes — useful for JEE/CUET line problems.)

---

NCERT Question.19 : Using the equation of a line, prove that the points $(3,0),\ (-2,-2),\ (8,2)$ are collinear.

Solution :
Find the equation of the line through $(3,0)$ and $(-2,-2)$.
Slope of line :
$$m=\frac{-2-0}{-2-3}=\frac{-2}{-5}=\frac{2}{5}$$
Point–slope from $(3,0)$:
$$y-0=\frac{2}{5}(x-3)\quad\Longrightarrow\quad 5y=2x-6$$
Rearrange:
$$2x-5y-6=0\quad\text{(or }2x-5y=6\text{).}$$
Check $(8,2)$:
$$2(8)-5(2)=16-10=6,$$
which satisfies the equation. Hence $(8,2)$ lies on the same line, so all three points are collinear.

(Collinearity check — worked by Anand Classes for coordinate geometry practice.)