Anand Classes provides NCERT Solutions for Class 11 Maths Chapter 3 – Trigonometric Functions (Exercise 3.1) with step-by-step explanations and detailed derivations as per the latest CBSE syllabus and NCERT textbook. These solutions help students understand domain, range, and fundamental trigonometric identities, ensuring a strong conceptual base for competitive exams like JEE, NDA, and CUET. Each question is solved with clarity and accuracy to help students score full marks in exams. Click the print button to download study material and notes in PDF format.
Q.1 : Find the radian measures corresponding to the following degree measures:
(i) 25° (ii) -47°30′ (iii) 240° (iv) 520°
Solution:
(i) We know that
$$180^\circ = \pi \text{ rad}$$
So,
$$1^\circ = \frac{\pi}{180} \text{ rad}$$
Hence,
$$25^\circ = \frac{\pi}{180} \times 25 = \frac{5\pi}{36} \text{ rad}$$
(ii) We know that
$$60′ = 1^\circ \implies 30′ = \frac{1}{2}^\circ$$
So,
$$-47^\circ 30′ = -47\frac{1}{2}^\circ = -\frac{95}{2}^\circ$$
Converting to radians:
$$-\frac{95}{2} \cdot \frac{\pi}{180} = -\frac{19\pi}{72} \text{ rad}$$
(iii)
$$240^\circ = 240 \cdot \frac{\pi}{180} = \frac{4\pi}{3} \text{ rad}$$
(iv)
$$520^\circ = 520 \cdot \frac{\pi}{180} = \frac{26\pi}{9} \text{ rad}$$
Hence, the radian measures are:
$$(i) \frac{5\pi}{36}, \quad (ii) -\frac{19\pi}{72}, \quad (iii) \frac{4\pi}{3}, \quad (iv) \frac{26\pi}{9}$$
Q.2 : Find the degree measures corresponding to the following radian measures (Use $\pi = 22/7$):
(i) $\frac{11}{16}$ (ii) $-4$ (iii) $\frac{5\pi}{3}$ (iv) $\frac{7\pi}{6}$
Solution:
(i)
$$\frac{11}{16} \text{ rad} = \frac{11}{16} \cdot \frac{180^\circ}{\pi}$$
$$= \frac{11}{16} \cdot \frac{180 \cdot 7}{22}$$
$$= \frac{11 \cdot 180 \cdot 7}{16 \cdot 22} = \frac{315}{8}^\circ = 39\frac{3}{8}^\circ$$
Separating degrees, minutes, and seconds:
$$39\frac{3}{8}^\circ = 39^\circ + \frac{3}{8}^\circ$$
$$\frac{3}{8}^\circ \cdot 60′ = 22.5′ = 22′ + 0.5’$$
$$0.5′ \cdot 60” = 30”$$
Hence,
$$\frac{11}{16} \text{ rad} = 39^\circ 22′ 30”$$
(ii)
$$-4 \text{ rad} = -4 \cdot \frac{180^\circ}{\pi} = -4 \cdot \frac{180 \cdot 7}{22} = -229\frac{1}{11}^\circ$$
Separating degrees, minutes, and seconds:
$$\frac{1}{11}^\circ \cdot 60′ = 5\frac{5}{11}’ = 5′ + \frac{5}{11}’$$
$$\frac{5}{11}’ \cdot 60” = 27”$$
Hence,
$$-4 \text{ rad} = -229^\circ 5′ 27”$$
(iii)
$$\frac{5\pi}{3} \text{ rad} = \frac{5\pi}{3} \cdot \frac{180^\circ}{\pi} = \frac{5 \cdot 180}{3}^\circ = 300^\circ$$
(iv)
$$\frac{7\pi}{6} \text{ rad} = \frac{7\pi}{6} \cdot \frac{180^\circ}{\pi} = \frac{7 \cdot 180}{6}^\circ = 210^\circ$$
Hence, the degree measures are:
$$(i) 39^\circ 22′ 30”, \quad (ii) -229^\circ 5′ 27”, \quad (iii) 300^\circ, \quad (iv) 210^\circ$$
Q.3 : A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?
Solution:
Number of revolutions made by wheel in one minute (60 seconds) = 360
Number of revolutions made by wheel in one second $=\frac{360}{60} = 6$
Angle (in radians) the wheel turns in one revolution = $360^\circ = 2\pi \text{ radians}$
Angle (in radians) the wheel turns in 6 revolutions = $2\pi \times 6 = 12\pi$
Hence, the wheel turns = $12\pi \text{ radians in one second.}$
Q.4 : Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm (Use $\pi = 22/7$).
Solution:
Angle subtended by an arc at the centre of a circle = $\theta = \frac{l}{r} \text{ radians}$
Where $l$ = length of arc, $r$ = radius of circle.
Substitute values:
$$\theta = \frac{22}{100} \text{ radians}$$
Convert to degrees:
$$\theta = \frac{22}{100} \cdot \frac{180}{\pi} = \frac{22}{100} \cdot 180 \cdot \frac{7}{22} = \frac{126}{10} = 12.6^\circ$$
Separating degrees and minutes:
$$12.6^\circ = 12^\circ + 0.6^\circ$$
$$0.6^\circ \cdot 60′ = 36’$$
Hence, the angle is: $12^\circ 36’$
Q.5 : In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.
Solution:
Radius of the circle = $r = \frac{40}{2} = 20 \text{ cm}$
Length of chord = $AB = 20 \text{ cm}$
Let the centre be (O) and the chord be (AB).
$$AO = BO = 20 \text{ cm (radii)}$$
Since (AB = AO = BO), ($\triangle AOB$) is equilateral.
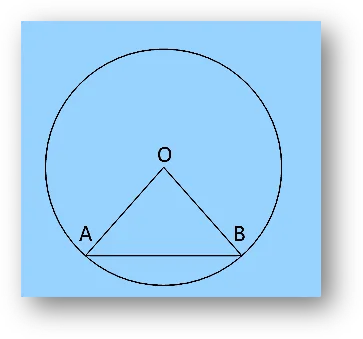
Hence,
$$\angle AOB = 60^\circ = 60 \times \frac{\pi}{180} = \frac{\pi}{3} \text{ radians}$$
Length of minor arc (AB = l):
$$\theta = \frac{l}{r} \implies \frac{\pi}{3} = \frac{l}{20} \implies l = \frac{20\pi}{3} \text{ cm}$$
Answer: $l = \frac{20\pi}{3} \text{ cm}$
Q.6 : If in two circles, arcs of the same length subtend angles (60o) and (75o) at the centre, find the ratio of their radii.
Solution:
Let radii of the two circles be ($r_1$) and ($r_2$), and the subtended angles be:
$$\theta_1 = 60^\circ = \frac{\pi}{3} \text{ rad}, \quad \theta_2 = 75^\circ = \frac{5\pi}{12} \text{ rad}$$
Since arcs are equal:
$$l = r_1 \theta_1 = r_2 \theta_2 \implies r_1 \cdot \frac{\pi}{3} = r_2 \cdot \frac{5\pi}{12} \implies \frac{r_1}{r_2} = \frac{5}{4}$$
Answer: $r_1 : r_2 = 5 : 4$
Q.7 : Find the angle in radians through which a pendulum swings if its length is 75 cm and the tip describes an arc of length: (i) 10 cm, (ii) 15 cm, (iii) 21 cm
Solution:
Radius of the pendulum = $r = 75 \text{ cm}$
(i) Arc length = 10 cm:
$$\theta = \frac{l}{r} = \frac{10}{75} = \frac{2}{15} \text{ rad}$$
(ii) Arc length = 15 cm:
$$\theta = \frac{l}{r} = \frac{15}{75} = \frac{1}{5} \text{ rad}$$
(iii) Arc length = 21 cm:
$$\theta = \frac{l}{r} = \frac{21}{75} = \frac{7}{25} \text{ rad}$$
Answers:
$$(i) \frac{2}{15} \text{ rad}, \quad (ii) \frac{1}{5} \text{ rad}, \quad (iii) \frac{7}{25} \text{ rad}$$


