Anand Classes provides comprehensive NCERT Solutions for Vector Algebra Miscellaneous Exercise of Chapter 10 for Class 12 Maths, designed to help students understand vector concepts with clarity and precision. These notes cover step-by-step solutions, important formulas, and exam-oriented explanations that make complex problems easier to grasp. Ideal for CBSE board preparation, this study material ensures accuracy, conceptual strength, and faster revision for scoring higher marks. Click the print button to download study material and notes.
NCERT Question.1 : Write down a unit vector in the XY-plane making an angle of $30^\circ$ with the positive direction of the x-axis.
Solution
A unit vector in the XY-plane making an angle $\theta$ with the positive direction of the x-axis is
$$\hat{r}=\cos\theta\;\hat{i} + \sin\theta\;\hat{j}$$
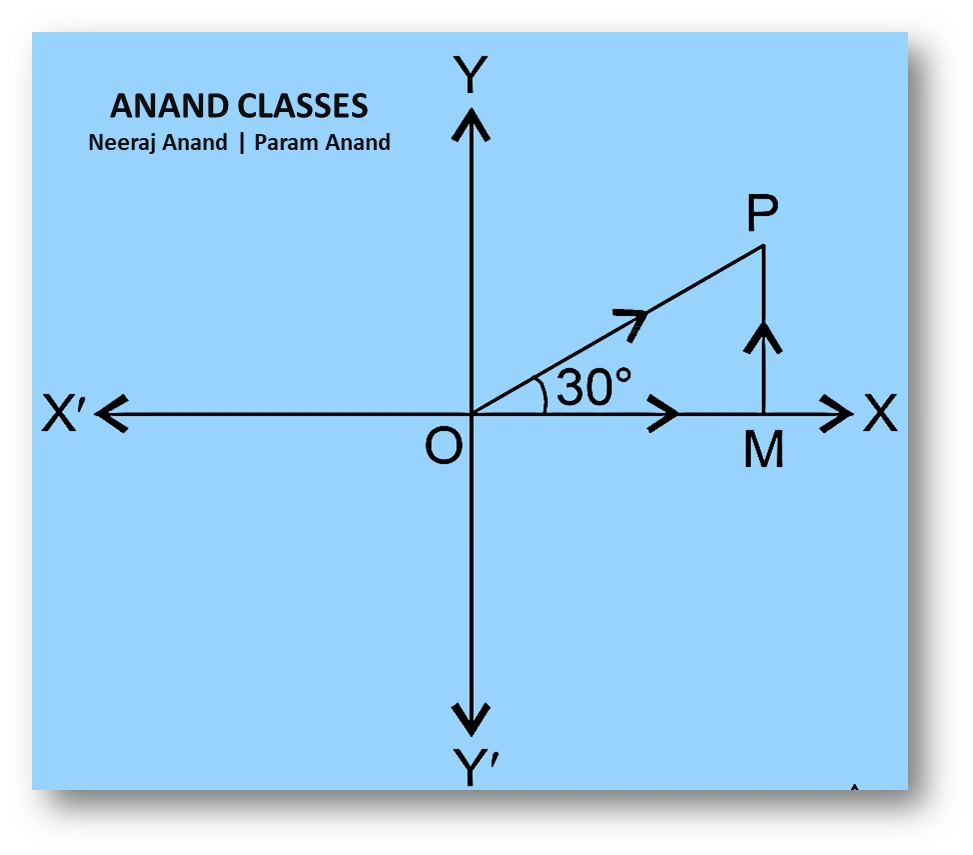
Given
$$\theta = 30^\circ$$
Substitute the value
$$\hat{r}=\cos 30^\circ\hat{i} + \sin 30^\circ\hat{j}$$
Using
$$\cos 30^\circ = \frac{\sqrt{3}}{2}, \qquad \sin 30^\circ = \frac{1}{2}$$
The required unit vector is
$$\hat{r}=\frac{\sqrt{3}}{2}\hat{i} + \frac{1}{2}\hat{j}$$
Final Result
$$\boxed{\frac{\sqrt{3}}{2}\hat{i} + \frac{1}{2}\hat{j}}$$
Strengthen your vector algebra concepts with clear and accurate NCERT solutions from Anand Classes, perfect for CBSE and JEE aspirants looking for reliable study material and crisp conceptual understanding.
NCERT Question 2 : Find the scalar components and magnitude of the vector joining the points
$P(x_1,y_1,z_1)$ and $Q(x_2,y_2,z_2)$.
Solution
The vector joining points $P$ and $Q$ is
$$\overrightarrow{PQ} = \text{Position vector of } Q\; -\; \text{Position vector of } P$$
So,
$$\overrightarrow{PQ} = (x_2 – x_1)\hat{i} + (y_2 – y_1)\hat{j} + (z_2 – z_1)\hat{k}$$
The magnitude of $\vec{PQ}$ is
$$|\overrightarrow{PQ}| = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2 + (z_2 – z_1)^2}$$
Scalar Components
$${x_2 – x_1, y_2 – y_1, z_2 – z_1}$$
Magnitude
$$\sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2 + (z_2 – z_1)^2}$$
Strengthen your understanding of 3D geometry and vectors with clear explanations from Anand Classes, ideal for JEE and CBSE students aiming for excellence.
NCERT Question.3 : A girl walks $4\text{ km}$ towards west, then she walks $3\text{ km}$ in a direction $30^\circ$ east of north and stops. Determine the girl’s displacement from her initial point of departure.
Solution
Let the initial point be the origin $O$.
Take North as the positive $y$-axis and East as the positive $x$-axis.
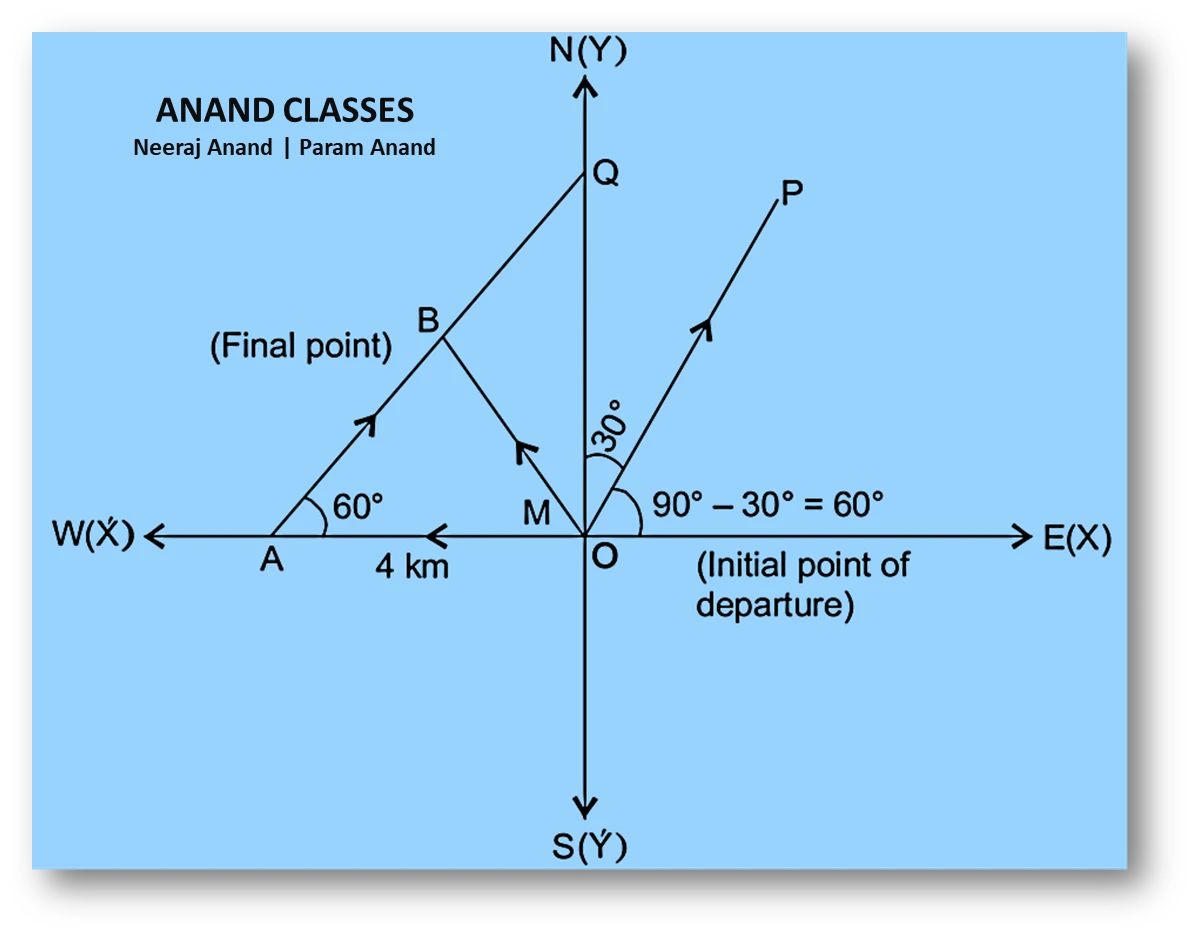
First displacement
She walks $4\text{ km}$ west, which is along the negative $x$-axis:
$$\vec{d_1} = -4\hat{i}$$
Second displacement
She walks $3\text{ km}$ in a direction $30^\circ$ east of north.
Angle with the positive $x$-axis:
$$90^\circ – 30^\circ = 60^\circ$$
So,
$$\vec{d_2} = 3\cos 60^\circ \hat{i} + 3\sin 60^\circ \hat{j}$$
$$\vec{d_2} = \frac{3}{2}\hat{i} + \frac{3\sqrt{3}}{2}\hat{j}$$
Total displacement
$$\vec{d} = \vec{d_1} + \vec{d_2}$$
$$\vec{d} = -4\hat{i} + \left(\frac{3}{2}\hat{i} + \frac{3\sqrt{3}}{2}\hat{j}\right)$$
$$\vec{d} = -\frac{5}{2}\hat{i} + \frac{3\sqrt{3}}{2}\hat{j}$$
Magnitude of displacement
$$|\vec{d}| = \sqrt{\left(-\frac{5}{2}\right)^2 + \left(\frac{3\sqrt{3}}{2}\right)^2}$$
$$|\vec{d}| = \sqrt{\frac{25}{4} + \frac{27}{4}}$$
$$|\vec{d}| = \sqrt{\frac{52}{4}}$$
$$|\vec{d}| = \sqrt{13}\text{ km}$$
Final Answer
Displacement vector:
$$\vec{d} = -\frac{5}{2}\hat{i} + \frac{3\sqrt{3}}{2}\hat{j}$$
Magnitude:
$$\sqrt{13}\text{ km}$$
Enhance your vector algebra skills with detailed explanations from Anand Classes — perfect for CBSE and JEE preparation with high-quality study notes.
NCERT Question.4 If $\vec{a}=\vec{b}+\vec{c}$, is it true that $|\vec{a}|=|\vec{b}|+|\vec{c}|$? Justify your answer.
Solution
Use the triangle inequality. For any vectors $\vec{b},\vec{c}$ we have
$$
|\vec{b}+\vec{c}| \le |\vec{b}|+|\vec{c}|.
$$
Thus if $\vec{a}=\vec{b}+\vec{c}$ then
$$
|\vec{a}| \le |\vec{b}|+|\vec{c}|.
$$
So equality is not guaranteed in general.
To find when equality holds, square both sides. Note
$$
|\vec{b}+\vec{c}|^2 = |\vec{b}|^2+|\vec{c}|^2+2\vec{b}\cdot\vec{c}.
$$
Compare with
$$
(|\vec{b}|+|\vec{c}|)^2 = |\vec{b}|^2+|\vec{c}|^2+2|\vec{b}||\vec{c}|.
$$
Equality $|\vec{b}+\vec{c}|=|\vec{b}|+|\vec{c}|$ requires
$$
\vec{b}\cdot\vec{c}=|\vec{b}||\vec{c}|.
$$
That means $\cos\theta=1$, so the angle $\theta$ between $\vec{b}$ and $\vec{c}$ is $0$. In words, equality holds iff $\vec{b}$ and $\vec{c}$ are collinear and point in the same direction.
A simple counterexample showing the statement is false in general is
$$
\vec{b}=\hat{i},\qquad \vec{c}=\hat{j}.
$$
Then $\vec{a}=\hat{i}+\hat{j}$, and
$$
|\vec{a}|=\sqrt{2}\ne 2=|\vec{b}|+|\vec{c}|.
$$
Final Answer
No, not always. In general
$$
|\vec{a}| \le |\vec{b}|+|\vec{c}|
$$
with equality iff $\vec{b}$ and $\vec{c}$ are collinear and point in the same direction.
Hence it is not true that $|\vec{a}|=|\vec{b}|+|\vec{c}|$
For polished, exam-ready explanations and more solved vector problems, check out the study material from Anand Classes, designed to help CBSE and JEE students master concepts quickly and confidently.
NCERT Question 5 : Find the value of $x$ for which the vector $\vec{a} = x(\hat{i} + \hat{j} + \hat{k})$ is a unit vector.
Solution
Understand the condition for a unit vector
A vector is a unit vector if its magnitude is equal to $1$.
The magnitude of a vector $\vec{v} = a\hat{i} + b\hat{j} + c\hat{k}$ is
$$|\vec{v}| = \sqrt{a^2 + b^2 + c^2}$$
Express the given vector
The given vector is
$$\vec{a} = x(\hat{i} + \hat{j} + \hat{k}) = x\hat{i} + x\hat{j} + x\hat{k}$$
Calculate the magnitude of the vector
$$|\vec{a}| = \sqrt{x^2 + x^2 + x^2}$$
$$|\vec{a}| = \sqrt{3x^2}$$
$$|\vec{a}| = |x|\sqrt{3}$$
Apply the unit vector condition
Since $\vec{a}$ is a unit vector,
$$|\vec{a}| = 1$$
$$|x|\sqrt{3} = 1$$
Solve for $x$
$$|x| = \frac{1}{\sqrt{3}}$$
$$x = \pm \frac{1}{\sqrt{3}}$$
Final Vector
Thus, the value of $x$ for which the given vector is a unit vector is
$$x = \pm \frac{1}{\sqrt{3}}$$
NCERT Question.6 : Find a vector of magnitude $5$ units, parallel to the resultant of the vectors
$\vec{a} = 2\hat{i} + 3\hat{j} – \hat{k}$ and $\vec{b} = \hat{i} – 2\hat{j} + \hat{k}$.
Solution
Find the resultant vector
Let $\vec{c}$ be the resultant vector.
$$\vec{c} = \vec{a} + \vec{b}$$
$$\vec{c} = (2\hat{i} + 3\hat{j} – \hat{k}) + (\hat{i} – 2\hat{j} + \hat{k})$$
$$\vec{c} = 3\hat{i} + \hat{j}$$
Find the unit vector in the direction of $\vec{c}$
$$|\vec{c}| = \sqrt{3^2 + 1^2} = \sqrt{10}$$
The unit vector in the direction of $\vec{c}$ is
$$\hat{c} = \frac{3\hat{i} + \hat{j}}{\sqrt{10}} = \frac{3}{\sqrt{10}}\hat{i} + \frac{1}{\sqrt{10}}\hat{j}$$
Find the vector with magnitude 5 units
Multiply the unit vector by $5$:
$$5\hat{c} = 5\left(\frac{3}{\sqrt{10}}\hat{i} + \frac{1}{\sqrt{10}}\hat{j}\right)$$
$$5\hat{c} = \frac{15}{\sqrt{10}}\hat{i} + \frac{5}{\sqrt{10}}\hat{j}$$
In simplified radical form:
$$\frac{3\sqrt{10}}{2}\hat{i} + \frac{\sqrt{10}}{2}\hat{j}$$
Prepare for vector algebra, CBSE exams, and JEE fundamentals with well-structured study notes from Anand Classes. These detailed explanations help strengthen core mathematical concepts and improve exam performance with clarity and accuracy.
NCERT Question.7 : If $\vec{a} = \hat{i} + \hat{j} + \hat{k}$,
$\vec{b} = 2\hat{i} – \hat{j} + 3\hat{k}$ and
$\vec{c} = \hat{i} – 2\hat{j} + \hat{k}$,
find a unit vector parallel to the vector $2\vec{a} – \vec{b} + 3\vec{c}$.
Solution
Step 1: Calculate the resultant vector
$$\vec{r} = 2\vec{a} – \vec{b} + 3\vec{c}$$
Substitute the given vectors:
$$\vec{r} = 2(\hat{i} + \hat{j} + \hat{k}) – (2\hat{i} – \hat{j} + 3\hat{k}) + 3(\hat{i} – 2\hat{j} + \hat{k})$$
Distribute the scalars:
$$(2\hat{i} + 2\hat{j} + 2\hat{k}) – (2\hat{i} – \hat{j} + 3\hat{k}) + (3\hat{i} – 6\hat{j} + 3\hat{k})$$
Combine like components:
$$\vec{r} = (2 – 2 + 3)\hat{i} + (2 + 1 – 6)\hat{j} + (2 – 3 + 3)\hat{k}$$
$$\vec{r} = 3\hat{i} – 3\hat{j} + 2\hat{k}$$
Step 2: Find the magnitude of $\vec{r}$
$$|\vec{r}| = \sqrt{3^2 + (-3)^2 + 2^2}$$
$$|\vec{r}| = \sqrt{9 + 9 + 4}$$
$$|\vec{r}| = \sqrt{22}$$
Step 3: Find the unit vector parallel to $\vec{r}$
$$\hat{r} = \frac{\vec{r}}{|\vec{r}|}$$
$$\hat{r} = \frac{3\hat{i} – 3\hat{j} + 2\hat{k}}{\sqrt{22}}$$
$$\hat{r} = \frac{3}{\sqrt{22}}\hat{i} – \frac{3}{\sqrt{22}}\hat{j} + \frac{2}{\sqrt{22}}\hat{k}$$
Strengthen your understanding of vectors with clear, structured explanations from Anand Classes. Perfect for CBSE Class 11, Class 12, and JEE preparation, these high-quality notes help you master concepts with ease and score better in exams.
NCERT Question.8 : Show that the points $A(1,-2,-8), B(5,0,-2)$ and $C(11,3,7)$ are collinear, and find the ratio in which $B$ divides $AC$.
Solution
Write position vectors for the points and form the side vectors.
$$
\vec a=\hat{i}-2\hat{j}-8\hat{k},\qquad
\vec b=5\hat{i}+0\hat{j}-2\hat{k},\qquad
\vec c=11\hat{i}+3\hat{j}+7\hat{k}
$$
Compute the vectors between the points.
$$
\vec{AB}=\vec b-\vec a=(5-1)\hat{i}+(0-(-2))\hat{j}+(-2-(-8))\hat{k}
=4\hat{i}+2\hat{j}+6\hat{k}
$$
$$
\vec{BC}=\vec c-\vec b=(11-5)\hat{i}+(3-0)\hat{j}+(7-(-2))\hat{k}
=6\hat{i}+3\hat{j}+9\hat{k}
$$
$$
\vec{AC}=\vec c-\vec a=(11-1)\hat{i}+(3-(-2))\hat{j}+(7-(-8))\hat{k}
=10\hat{i}+5\hat{j}+15\hat{k}
$$
Note the proportionality between the vectors. For example,
$$
\vec{BC}=\frac{3}{2}\vec{AB}
$$
and
$$
\vec{AC}=\vec{AB}+\vec{BC}=\Big(1+\frac{3}{2}\Big)\vec{AB}=\frac{5}{2}\vec{AB}.
$$
Because $\vec{AB}$, $\vec{BC}$ and $\vec{AC}$ are scalar multiples of one another, the three points $A,B,C$ are collinear.
To find the ratio in which $B$ divides $AC$, compare the lengths of $\vec{AB}$ and $\vec{BC}$ (or use the scalar multiple):
$$
\vec{BC}=\frac{3}{2}\vec{AB}\quad\Longrightarrow\quad |\vec{AB}|:|\vec{BC}|=1:\frac{3}{2}=2:3.
$$
Hence $B$ divides $AC$ internally in the ratio
$$\boxed{AB:BC = 2:3.}$$
Prepare confidently for CBSE and JEE with concise, stepwise geometry and vector solutions from Anand Classes, perfect for revision and exam practice.
NCERT Question.9 : Find the position vector of a point $R$ which divides the line joining two points $P$ and $Q$, whose position vectors are $\vec a$ and $\vec b$ respectively, externally in the ratio $1:2$. Also, show that $P$ is the mid-point of the line segment $RQ.
Solution
Use the external division formula to find the position vector of $R$.
Given
Two points $P$ and $Q$, whose position vectors are $\vec a$ and $\vec b$ respectively, divifde externally in the ratio $1:2$.
For external division:
$$
\vec r=\frac{m\vec q-n\vec p}{m-n}
$$
Substitute $m=1, n=2, (\vec p=\vec a), (\vec q=\vec b)$:
$$
\vec r=\frac{1\vec b-2\vec a}{1-2}
$$
$$
\vec r=\frac{\vec b-2\vec a}{-1}
$$
$$
\vec r=2\vec a-\vec b
$$
Thus the position vector of point $R$ is
$$
\boxed{2\vec a-\vec b}.
$$
Show that $P$ is the mid-point of $RQ$
Position vectors:
$R \rightarrow 2\vec a-\vec b$,
$Q \rightarrow \vec b$.
Mid-point of $RQ$:
$$
\frac{\vec r+\vec q}{2}
$$
$$
=\frac{(2\vec a-\vec b)+\vec b}{2}
$$
$$
=\frac{2\vec a}{2}
$$
$$
=\vec a
$$
The mid-point of $RQ$ has position vector $(\vec a)$, which is exactly the position vector of $P$.
Hence, $P$ is the mid-point of line segment $RQ$.
Excel in vector algebra with concise, exam-oriented solutions from Anand Classes, ideal for CBSE and JEE preparation with clear MathJax-formatted explanations.


