Anand Classes presents well-structured NCERT Solutions for Exercise 10.2 of Chapter 10 Vector Algebra for Class 12 Mathematics, helping students strengthen their understanding of vector operations, scalar multiplication, and fundamental properties through clear, step-by-step explanations. These Set-2 notes follow the latest NCERT and CBSE guidelines, making them ideal for revision, concept clarity, and board exam preparation. Click the print button to download study material and notes.
NCERT Question.11 : Show that the vectors
$\vec{a} = 2\hat{i} – 3\hat{j} + 4\hat{k}$ and $\vec{b} = -4\hat{i} + 6\hat{j} – 8\hat{k}$ are collinear.
Solution
Given:
$$\vec{b} = -4\hat{i} + 6\hat{j} – 8\hat{k}$$
Notice that:
$$\vec{b} = -2(2\hat{i} – 3\hat{j} + 4\hat{k})$$
$$\vec{b} = -2\vec{a}$$
We know that two vectors are collinear if:
$$\vec{b} = \lambda \vec{a}$$
for some scalar $\lambda$.
Here, $\lambda = -2$.
Hence, the vectors $\vec{a}$ and $\vec{b}$ are collinear.
Final Result
$$\boxed{\text{Vectors } \vec{a} \text{ and } \vec{b} \text{ are collinear}}$$
Master vector relationships and collinearity with Anand Classes’ detailed examples, perfect for CBSE and JEE preparation.
NCERT Question.12 : Find the direction cosines of the vector
$$\vec{a} = \hat{i} + 2\hat{j} + 3\hat{k}$$
Solution
Let
$$\vec{a} = \hat{i} + 2\hat{j} + 3\hat{k}$$
Magnitude of $\vec{a}$:
$$|\vec{a}| = \sqrt{1^2 + 2^2 + 3^2}$$
$$|\vec{a}| = \sqrt{1 + 4 + 9} = \sqrt{14}$$
Direction cosines $(\ell, m, n)$ are given by:
$$
\ell = \frac{x}{|\vec{a}|} = \frac{1}{\sqrt{14}}, \quad
m = \frac{y}{|\vec{a}|} = \frac{2}{\sqrt{14}}, \quad
n = \frac{z}{|\vec{a}|} = \frac{3}{\sqrt{14}}
$$
Thus, the direction cosines of $\vec{a}$ are:
$$(\ell, m, n) = \left(\frac{1}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}}\right)$$
Final Result
$$\boxed{\left(\frac{1}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}}\right)}$$
Sharpen your vector skills with step-by-step solutions and clear explanations from Anand Classes, ideal for CBSE and competitive exams like JEE.
NCERT Question.13 : Find the direction cosines of the vector joining the points $A(1,2,-3)$ and $B(-1,-2,1)$, in the direction from $A$ to $B$.
Solution
Let the position vectors of points $A$ and $B$ be $\overrightarrow{OA}$ and $\overrightarrow{OB}$ respectively.
The vector from $A$ to $B$ is:
$$\overrightarrow{AB} = \overrightarrow{OB} – \overrightarrow{OA}$$
Compute components:
$$
\overrightarrow{AB} = (-1-1)\hat{i} + (-2-2)\hat{j} + (1-(-3))\hat{k}
$$
$$
\overrightarrow{AB} = -2\hat{i} – 4\hat{j} + 4\hat{k}
$$
Magnitude of $\overrightarrow{AB}$:
$$
|\overrightarrow{AB}| = \sqrt{(-2)^2 + (-4)^2 + 4^2}
= \sqrt{4 + 16 + 16}
= \sqrt{36}
= 6
$$
Direction cosines:
$$
\ell = \frac{-2}{6} = -\frac{1}{3}, \quad
m = \frac{-4}{6} = -\frac{2}{3}, \quad
n = \frac{4}{6} = \frac{2}{3}
$$
Final Result
$$
\boxed{\left(-\frac{1}{3}, -\frac{2}{3}, \frac{2}{3}\right)}
$$
Strengthen your understanding of 3D vectors with Anand Classes’ comprehensive notes, perfect for CBSE and JEE preparation.
NCERT Question.14 :
Show that the vector $\vec{a} = \hat{i} + \hat{j} + \hat{k}$
is equally inclined to the axes $OX$, $OY$, and $OZ$.
Solution
Let
$$\vec{a} = \hat{i} + \hat{j} + \hat{k}$$
Magnitude of $\vec{a}$:
$$
|\vec{a}| = \sqrt{1^2 + 1^2 + 1^2} = \sqrt{3}
$$
Direction cosines:
$$
\ell = \frac{1}{|\vec{a}|} = \frac{1}{\sqrt{3}}, \quad
m = \frac{1}{|\vec{a}|} = \frac{1}{\sqrt{3}}, \quad
n = \frac{1}{|\vec{a}|} = \frac{1}{\sqrt{3}}
$$
Let $\alpha$, $\beta$, and $\gamma$ be the angles formed by vector $\vec{a}$ with the positive directions of the $x$, $y$, and $z$ axes respectively.
$$
\cos \alpha = \ell = \frac{1}{\sqrt{3}}, \quad
\cos \beta = m = \frac{1}{\sqrt{3}}, \quad
\cos \gamma = n = \frac{1}{\sqrt{3}}
$$
All angles $\alpha$, $\beta$, and $\gamma$ are equal.
Hence, the vector is equally inclined to $OX$, $OY$, and $OZ$.
Final Result
$$
\boxed{\text{Vector } \vec{a} \text{ is equally inclined to the axes OX, OY, and OZ}}
$$
Enhance your grasp of direction cosines and 3D vector geometry with Anand Classes’ clear and structured notes, perfect for CBSE and JEE preparation.
NCERT Question.15 : Find the position vector of a point $R$ which divides the line joining two points $P$ and $Q$ whose position vectors are
$$\vec{OP} = \hat{i} + 2\hat{j} – \hat{k} \quad \text{and} \quad \vec{OQ} = -\hat{i} + \hat{j} + \hat{k}$$
in the ratio $2:1$
(i) Internally (ii) Externally
Solution
Let the position vectors of $P$ and $Q$ be $\vec{OP}$ and $\vec{OQ}$ respectively:
$$\vec{OP} = \hat{i} + 2\hat{j} – \hat{k}, \quad \vec{OQ} = -\hat{i} + \hat{j} + \hat{k}$$
(i) Internally
Using the section formula (internal division):
$$\vec{OR} = \frac{2\vec{OQ} + 1\vec{OP}}{2+1}$$
Substitute the vectors:
$$\vec{OR} = \frac{2(-\hat{i} + \hat{j} + \hat{k}) + (\hat{i} + 2\hat{j} – \hat{k})}{3}$$
Simplify:
$$\vec{OR} = \frac{-2\hat{i} + 2\hat{j} + 2\hat{k} + \hat{i} + 2\hat{j} – \hat{k}}{3}$$
$$\vec{OR} = \frac{-\hat{i} + 4\hat{j} + \hat{k}}{3}$$
$$\vec{OR} = -\frac{1}{3}\hat{i} + \frac{4}{3}\hat{j} + \frac{1}{3}\hat{k}$$
(ii) Externally
Using the section formula (external division):
$$\vec{OR} = \frac{2\vec{OQ} – 1\vec{OP}}{2-1}$$
Substitute the vectors:
$$\vec{OR} = 2(-\hat{i} + \hat{j} + \hat{k}) – (\hat{i} + 2\hat{j} – \hat{k})$$
Simplify:
$$\vec{OR} = -2\hat{i} + 2\hat{j} + 2\hat{k} – \hat{i} – 2\hat{j} + \hat{k}$$
$$\vec{OR} = -3\hat{i} + 0\hat{j} + 3\hat{k}$$
$$\vec{OR} = -3\hat{i} + 3\hat{k}$$
Final Result
$$\boxed{
\text{(i) Internally: } \vec{OR} = -\frac{1}{3}\hat{i} + \frac{4}{3}\hat{j} + \frac{1}{3}\hat{k}, \quad
\text{(ii) Externally: } \vec{OR} = -3\hat{i} + 3\hat{k}
}$$
Enhance your understanding of vector division and position vectors with Anand Classes’ concise and clear solutions, ideal for CBSE and JEE preparation.
NCERT Question.16 : Find the position vector of the mid-point of the line joining the points $(2 , 3 , 4)$ and $(4 , 1 , -2)$.
Solution:
The midpoint divides the line joining the points $(2 , 3 , 4)$ and $(4 , 1 , -2)$ internally in the ratio $1:1$.
Using the midpoint formula, the position vector of the midpoint $R$ is:
$$
\vec{OR} = \frac{1(\vec{r}_2) + 1(\vec{r}_1)}{1+1}
$$
Substitute the position vectors:
$$
\vec{OR} = \frac{(2\hat{i} + 3\hat{j} + 4\hat{k}) + (4\hat{i} + \hat{j} – 2\hat{k})}{2}
$$
Simplify:
$$
\vec{OR} = \frac{(6\hat{i} + 4\hat{j} + 2\hat{k})}{2}
$$
$$
\vec{OR} = 3\hat{i} + 2\hat{j} + \hat{k}
$$
Final Result
$$
\boxed{\vec{OR} = 3\hat{i} + 2\hat{j} + \hat{k}}
$$
Strengthen your vector analysis skills with Anand Classes’ step-by-step solutions, perfect for CBSE and JEE preparation.
NCERT Question.17 : Show that the points $A$, $B$, and $C$ with position vectors
$\vec{a} = 3\hat{i} – 4\hat{j} – 4\hat{k}$,
$\vec{b} = 2\hat{i} – \hat{j} + \hat{k}$, and
$\vec{c} = \hat{i} – 3\hat{j} – 5\hat{k}$
form the vertices of a right-angled triangle.
Solution:
Position vectors of points $A$, $B$, and $C$ are given as:
$$
\vec{a} = 3\hat{i} – 4\hat{j} – 4\hat{k}, \quad
\vec{b} = 2\hat{i} – \hat{j} + \hat{k}, \quad
\vec{c} = \hat{i} – 3\hat{j} – 5\hat{k}
$$
The vectors representing the sides of the triangle are:
$$
\vec{AB} = \vec{b} – \vec{a} = (2-3)\hat{i} + (-1+4)\hat{j} + (1+4)\hat{k} = -\hat{i} + 3\hat{j} + 5\hat{k}
$$
$$
\vec{BC} = \vec{c} – \vec{b} = (1-2)\hat{i} + (-3+1)\hat{j} + (-5-1)\hat{k} = -\hat{i} – 2\hat{j} – 6\hat{k}
$$
$$
\vec{CA} = \vec{a} – \vec{c} = (3-1)\hat{i} + (-4+3)\hat{j} + (-4+5)\hat{k} = 2\hat{i} – \hat{j} + \hat{k}
$$
Now, calculate the squares of their magnitudes:
$$
|\vec{AB}|^2 = (-1)^2 + 3^2 + 5^2 = 1 + 9 + 25 = 35
$$
$$
|\vec{BC}|^2 = (-1)^2 + (-2)^2 + (-6)^2 = 1 + 4 + 36 = 41
$$
$$
|\vec{CA}|^2 = (2)^2 + (-1)^2 + (1)^2 = 4 + 1 + 1 = 6
$$
Check for the Pythagorean relation:
$$
|\vec{AB}|^2 + |\vec{CA}|^2 = 35 + 6 = 41 = |\vec{BC}|^2
$$
Since the sum of the squares of two sides equals the square of the third side, the triangle $ABC$ is right-angled at point $A$.
Final Result
$$
\boxed{\text{The points } A, B, C \text{ form a right-angled triangle at } A}
$$
Boost your vector problem-solving with Anand Classes’ detailed solutions, ideal for JEE and CBSE preparation.
NCERT Question.18 :
In triangle $ABC$, which of the following is not true:
(A) $\vec{AB} + \vec{BC} + \vec{CA} = \vec{0}$
(B) $\vec{AB} + \vec{BC} – \vec{AC} = \vec{0}$
(C) $\vec{AB} + \vec{BC} – \vec{CA} = \vec{0}$
(D) $\vec{AB} – \vec{CB} + \vec{CA} = \vec{0}$
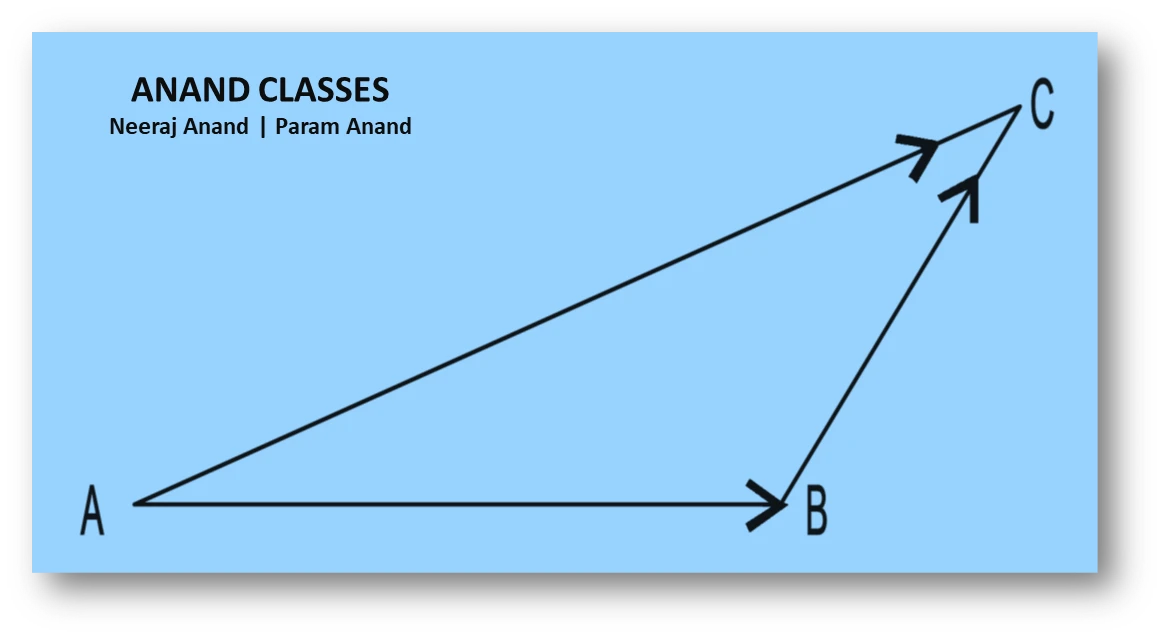
Solution:
Using the triangle law of vector addition,
$$
\vec{AB} + \vec{BC} = \vec{AC} \implies \vec{AB} + \vec{BC} – \vec{AC} = \vec{0}
$$
Also,
$$
\vec{AB} + \vec{BC} + \vec{CA} = \vec{0}
$$
Hence:
- Option A: $\vec{AB} + \vec{BC} + \vec{CA} = \vec{0}$ ✅ True
- Option B: $\vec{AB} + \vec{BC} – \vec{AC} = \vec{0}$ ✅ True
- Option D: $\vec{AB} – \vec{CB} + \vec{CA} = \vec{0}$ ✅ True
Option C states:
$$
\vec{AB} + \vec{BC} – \vec{CA} = \vec{0}
$$
This is not true, because $\vec{CA} = -\vec{AC}$, so this equation would incorrectly imply
$$
\vec{AB} + \vec{BC} + \vec{AC} = \vec{0} \quad \text{which is false.}
$$
Final Result
$$
\boxed{\text{The option which is not true is (C)}}
$$
Get thorough explanations and step-by-step solutions for all vector problems with Anand Classes, perfect for JEE and CBSE preparation.
NCERT Question.19 :
If $\vec{a}$ and $\vec{b}$ are two collinear vectors, then which of the following are incorrect?
(A) $\vec{b} = \lambda \vec{a}$, for some scalar $\lambda$
(B) $\vec{a} = \pm \vec{b}$
(C) The respective components of $\vec{a}$ and $\vec{b}$ are proportional
(D) Both the vectors $\vec{a}$ and $\vec{b}$ have the same direction, but different magnitudes
Solution:
If $\vec{a}$ and $\vec{b}$ are collinear, they are parallel. Therefore, for some scalar $\lambda$:
$$
\vec{b} = \lambda \vec{a}
$$
Hence, option A is true.
If $\lambda = \pm 1$, then
$$
\vec{a} = \pm \vec{b}
$$
Thus, option B is true.
Let
$$
\vec{a} = a_1 \hat{i} + a_2 \hat{j} + a_3 \hat{k}, \quad \vec{b} = b_1 \hat{i} + b_2 \hat{j} + b_3 \hat{k}
$$
Then
$$
\vec{b} = \lambda \vec{a} \implies b_1 \hat{i} + b_2 \hat{j} + b_3 \hat{k} = \lambda (a_1 \hat{i} + a_2 \hat{j} + a_3 \hat{k})
$$
Comparing components:
$$
b_1 = \lambda a_1, \quad b_2 = \lambda a_2, \quad b_3 = \lambda a_3
$$
Hence, the components of $\vec{a}$ and $\vec{b}$ are proportional, so option C is true.
Option D is incorrect, because collinear vectors can have same or opposite directions, and their magnitudes may or may not differ; it is not necessary that they always have the same direction with different magnitudes.
Final Result
$$
\boxed{\text{The incorrect option is (D)}}
$$
Download top-quality study material by Anand Classes for a complete understanding of vector properties, ideal for JEE and CBSE preparation.


