Anand Classes provides NCERT Solutions for Class 11 Maths Chapter 9 – Straight Lines (Exercise 9.1) for the 2025–2026 academic session, based on the latest NCERT and CBSE syllabus. These step-by-step solutions cover key concepts such as slope of a line, angle between two lines, and different forms of the equation of a line, helping students build a strong foundation in coordinate geometry. Each question is solved clearly with formulas and explanations to prepare students for CBSE Board Exams, JEE Main, JEE Advanced, NDA, and CUET. Click the print button to download study material and notes in PDF format.
NCERT Question.1 : Draw a quadrilateral in the Cartesian plane, whose vertices are $(-4,5),\ (0,7),\ (5,-5),$ and $(-4,-2)$. Also, find its area.
Solution:
Let’s consider the quadrilateral $ABCD$ with vertices $A(-4,5),\ B(0,7),\ C(5,-5)$ and $D(-4,-2)$.
After plotting the points on the Cartesian plane we get the required quadrilateral.
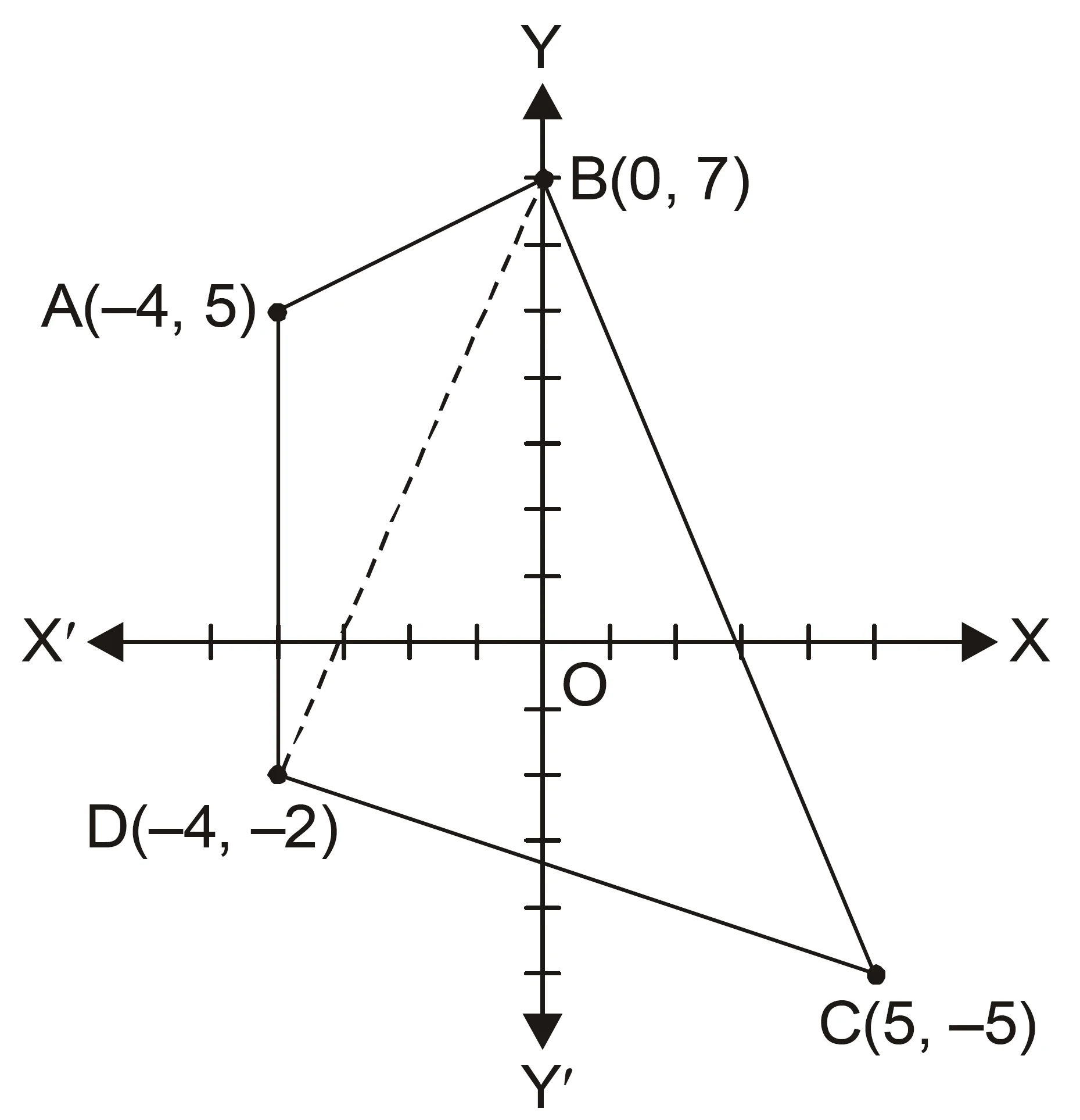
Construction: Join diagonal $AC$.
Area $(ABCD) =$ area $(\triangle ABC)$ $+$ area $(\triangle ADC)$.
The area of a triangle with vertices $(x_1,y_1),\ (x_2,y_2)$ and $(x_3,y_3)$ is
$$
\text{Area} = \left|\tfrac{1}{2}\big[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)\big]\right|.
$$
So,
$$
\text{Area}(\triangle ABC)=\left|\tfrac{1}{2}\big[-4(7-(-5)) + 0((-5)-5) + 5(5-7)\big]\right|
$$
$$
=\left|\tfrac{1}{2}\big[-4(12) + 5(-2)\big]\right|
$$
$$
=\left|\tfrac{1}{2}(-48 -10)\right|
$$
$$
=\left|\tfrac{1}{2}(-58)\right|
$$
$$
=29\ \text{sq. unit}.
$$
Next,
$$
\text{Area}(\triangle ACD)=\left|\tfrac{1}{2}\big[-4((-5)-(-2)) + 5((-2)-5) + (-4)(5-(-5))\big]\right|
$$
$$
=\left|\tfrac{1}{2}\big[-4(-3) + 5(-7) -4(10)\big]\right|
$$
$$
=\left|\tfrac{1}{2}\big[12 -35 -40\big]\right|
$$
$$
=\left|\tfrac{1}{2}(-63)\right|
$$
$$
=\frac{63}{2}\ \text{sq. unit}.
$$
Therefore,
$$
\text{Area}(ABCD) = 29 + \frac{63}{2} = \frac{121}{2}\ \text{sq. unit}.
$$
NCERT Question.2 : The base of an equilateral triangle with side $2a$ lies along the $y$-axis such that the mid-point of the base is at the origin. Find vertices of the triangle.
Solution:
Consider $\triangle ABC$ which is equilateral with side $2a$, so $AB=BC=AC=2a$.
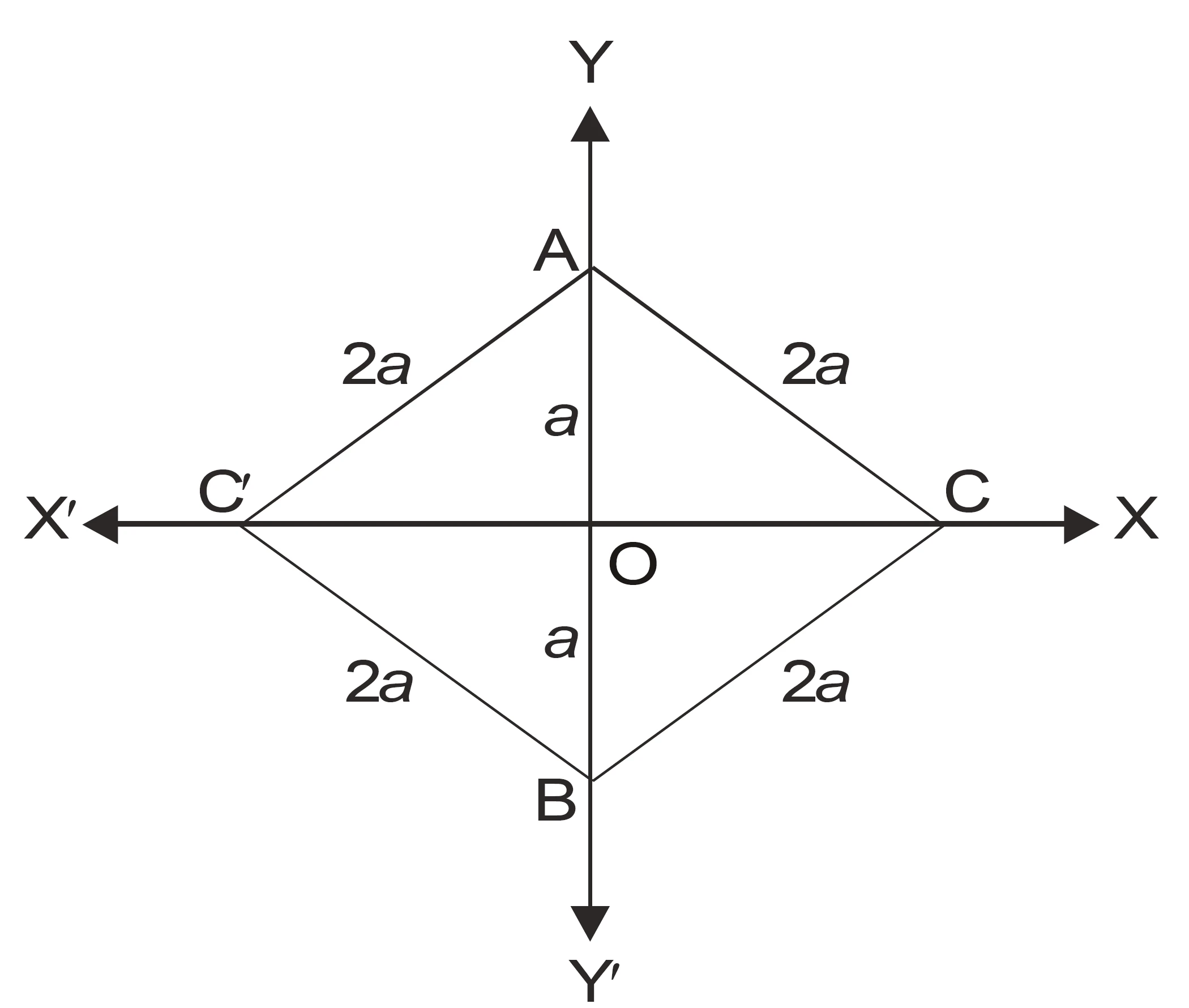
Assume $AB$ is the base and the origin is the midpoint of $AB$. Thus
$$
A=(0,a),\qquad B=(0,-a).
$$
The line joining the vertex $C$ and the origin lies on the $x$-axis. By Pythagoras on triangle formed by half the base and the side,
$$
(2a)^2 = a^2 + OC^2.
$$
So,
$$
4a^2 – a^2 = OC^2,
$$
$$
OC^2 = 3a^2,
$$
$$
OC = \sqrt{3}a.
$$
Hence the coordinates of $A$ are
$$
A=\big(\pm \sqrt{3}a,\ 0\big).
$$
Therefore the vertices of the equilateral triangle are
$$
(0,a),\ (0,-a),\ \big(\sqrt{3}a,0\big)
$$
or
$$
(0,a),\ (0,-a),\ \big(-\sqrt{3}a,0\big).
$$
NCERT Question.3 : Find the distance between $P(x_1, y_1)$ and $Q(x_2, y_2)$ when:
(i) $PQ$ is parallel to the $y$-axis
(ii) $PQ$ is parallel to the $x$-axis
Solution :
(i) When $PQ$ is parallel to the $y$-axis
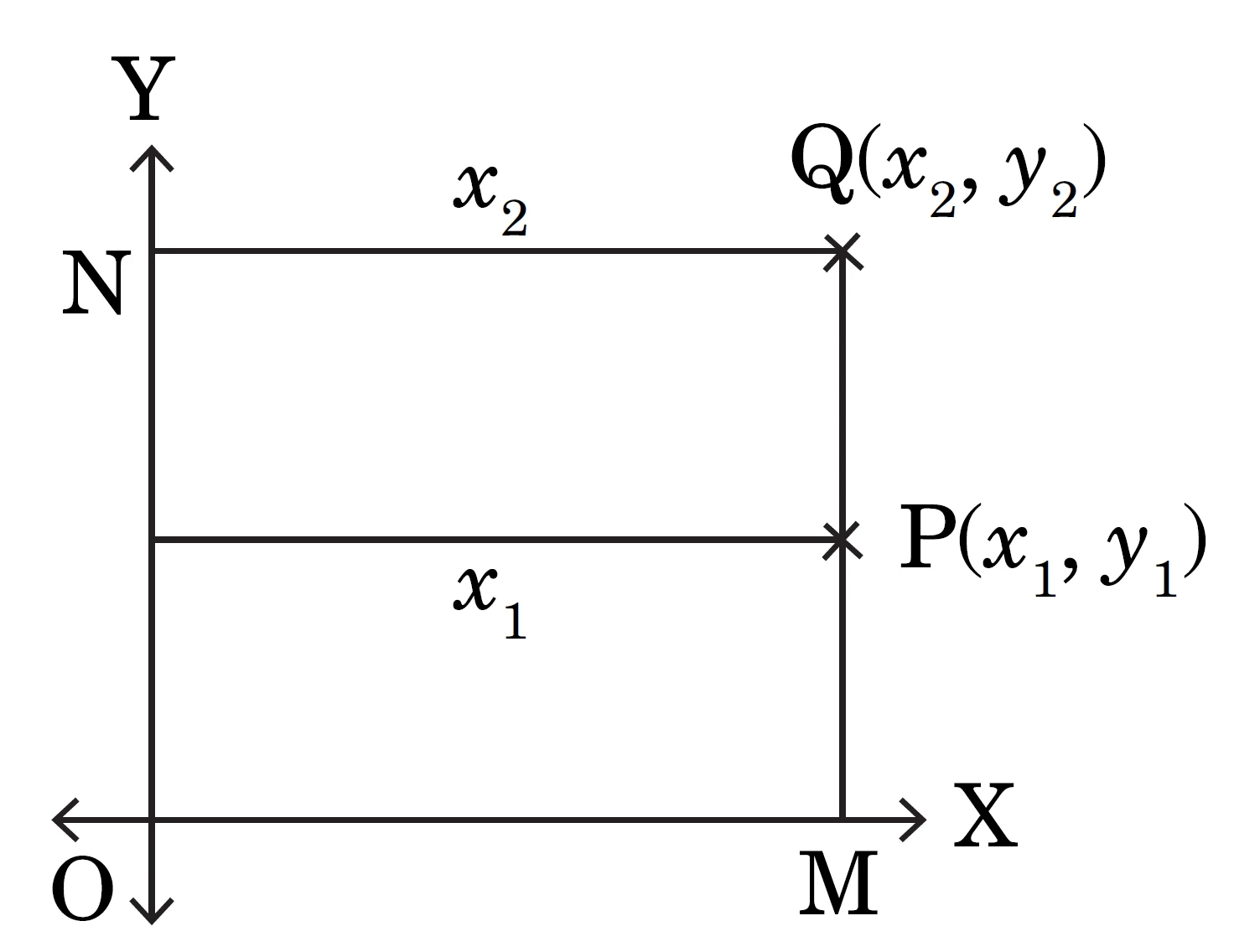
The $x$-coordinates are the same, so $x_1 = x_2$.
The distance between two points is given by
$$
PQ = \sqrt{(x_1 – x_2)^2 + (y_1 – y_2)^2}.
$$
Since $x_1 = x_2$,
$$
PQ = \sqrt{(y_1 – y_2)^2} = |y_1 – y_2|.
$$
(ii) When $PQ$ is parallel to the $x$-axis
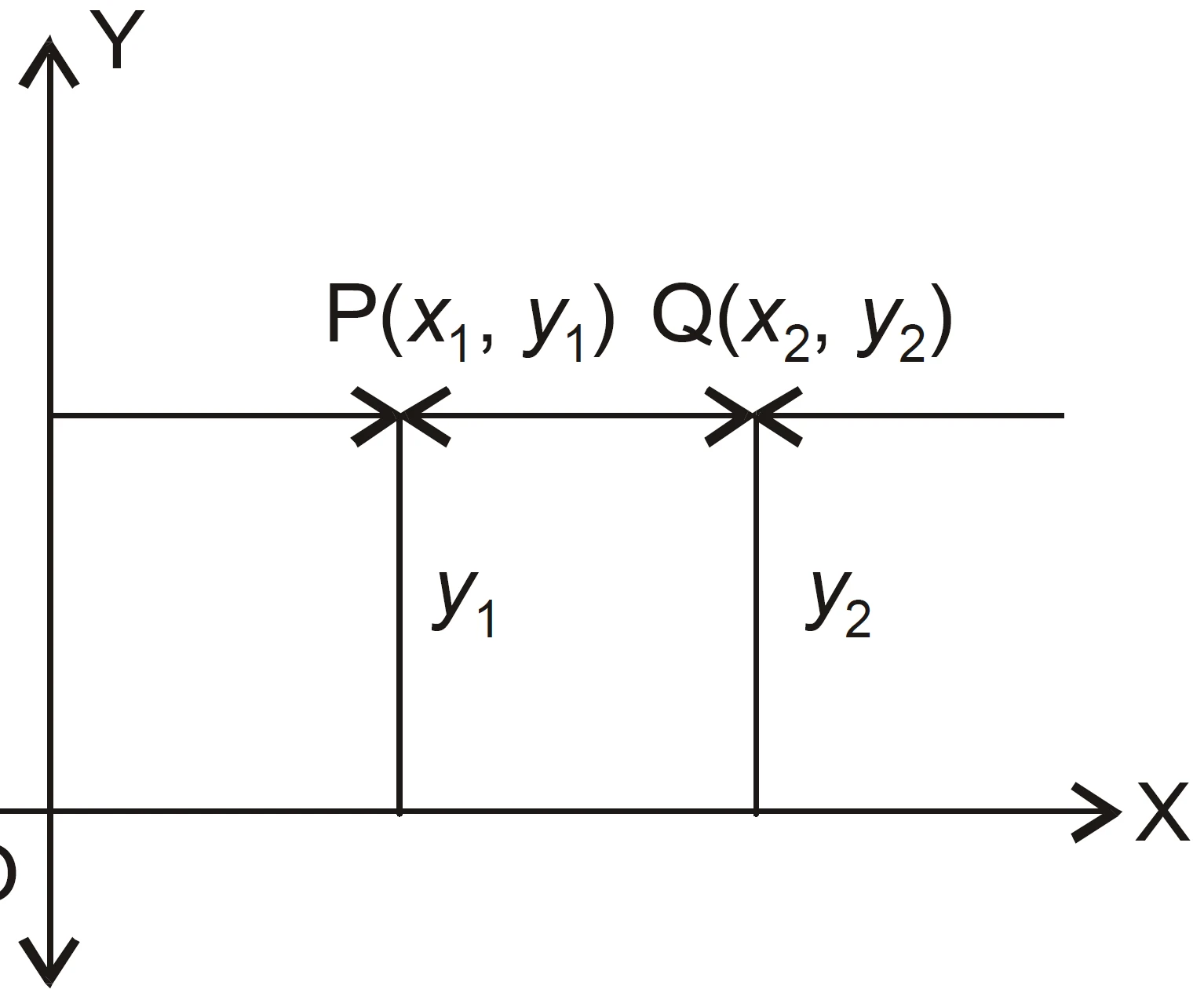
The $y$-coordinates are the same, so $y_1 = y_2$.
Again, the distance between two points is
$$
PQ = \sqrt{(x_1 – x_2)^2 + (y_1 – y_2)^2}.
$$
Since $y_1 = y_2$,
$$
PQ = \sqrt{(x_1 – x_2)^2} = |x_1 – x_2|.
$$
NCERT Question.4 : Find a point on the $x$-axis which is equidistant from the points $(7, 6)$ and $(3, 4)$.
Solution :
Let the required point be $P(a, 0)$ on the $x$-axis.
Since $P$ is equidistant from $A(7,6)$ and $B(3,4)$,
$$
PA = PB.
$$
Using the distance formula,
$$
\sqrt{(a – 7)^2 + (0 – 6)^2} = \sqrt{(a – 3)^2 + (0 – 4)^2}.
$$
Simplifying:
$$
\sqrt{(a – 7)^2 + 36} = \sqrt{(a – 3)^2 + 16}.
$$
Squaring both sides:
$$
(a – 7)^2 + 36 = (a – 3)^2 + 16.
$$
Expanding:
$$
a^2 – 14a + 49 + 36 = a^2 – 6a + 9 + 16.
$$
Simplifying:
$$
a^2 – 14a + 85 = a^2 – 6a + 25.
$$
$$
-14a + 85 = -6a + 25.
$$
$$
-8a = -60.
$$
$$
a = \frac{15}{2}.
$$
Hence, the point on the $x$-axis which is equidistant from $(7, 6)$ and $(3, 4)$ is
$$
\boxed{\left(\frac{15}{2}, 0\right)}.
$$
NCERT Question.5 : Find the slope of a line passing through the origin and the midpoint of the line segment joining the points $P(0, -4)$ and $B(8, 0)$.
Solution :
Let the coordinates of the midpoint of the line segment joining $P(0, -4)$ and $B(8, 0)$ be $(x, y)$.
$$
x = \frac{0 + 8}{2} = 4, \quad y = \frac{-4 + 0}{2} = -2
$$
So, the midpoint is $(4, -2)$.
The slope $m$ of the line passing through $(x_1, y_1)$ and $(x_2, y_2)$ is given by:
$$
m = \frac{y_2 – y_1}{x_2 – x_1}, \quad \text{where } x_2 \ne x_1
$$
Now, for the line passing through $(0, 0)$ and $(4, -2)$:
$$
m = \frac{-2 – 0}{4 – 0} = \frac{-2}{4} = -\frac{1}{2}
$$
Hence, the required slope is:
$$
\boxed{-\frac{1}{2}}
$$
NCERT Question.6 : Without using the Pythagoras theorem, show that the points $(4, 4)$, $(3, 5)$, and $(-1, -1)$ are the vertices of a right-angled triangle.
Solution :
Let the given points be $A(4, 4)$, $B(3, 5)$, and $C(-1, -1)$.
The slope of the line joining $(x_1, y_1)$ and $(x_2, y_2)$ is:
$$
m = \frac{y_2 – y_1}{x_2 – x_1}, \quad x_2 \ne x_1
$$
Slope of AB:
$$
m_1 = \frac{5 – 4}{3 – 4} = \frac{1}{-1} = -1
$$
Slope of AC:
$$
m_2 = \frac{-1 – 4}{-1 – 4} = \frac{-5}{-5} = 1
$$
Now,
$$
m_1 \cdot m_2 = (-1) \times (1) = -1
$$
Since the product of slopes is $-1$, the lines $AB$ and $AC$ are perpendicular.
Hence, $\triangle ABC$ is a right-angled triangle at vertex $A(4, 4)$.
NCERT Question.7 : Find the slope of the line which makes an angle of $30^\circ$ with the positive direction of the y-axis measured anticlockwise.
Solution :
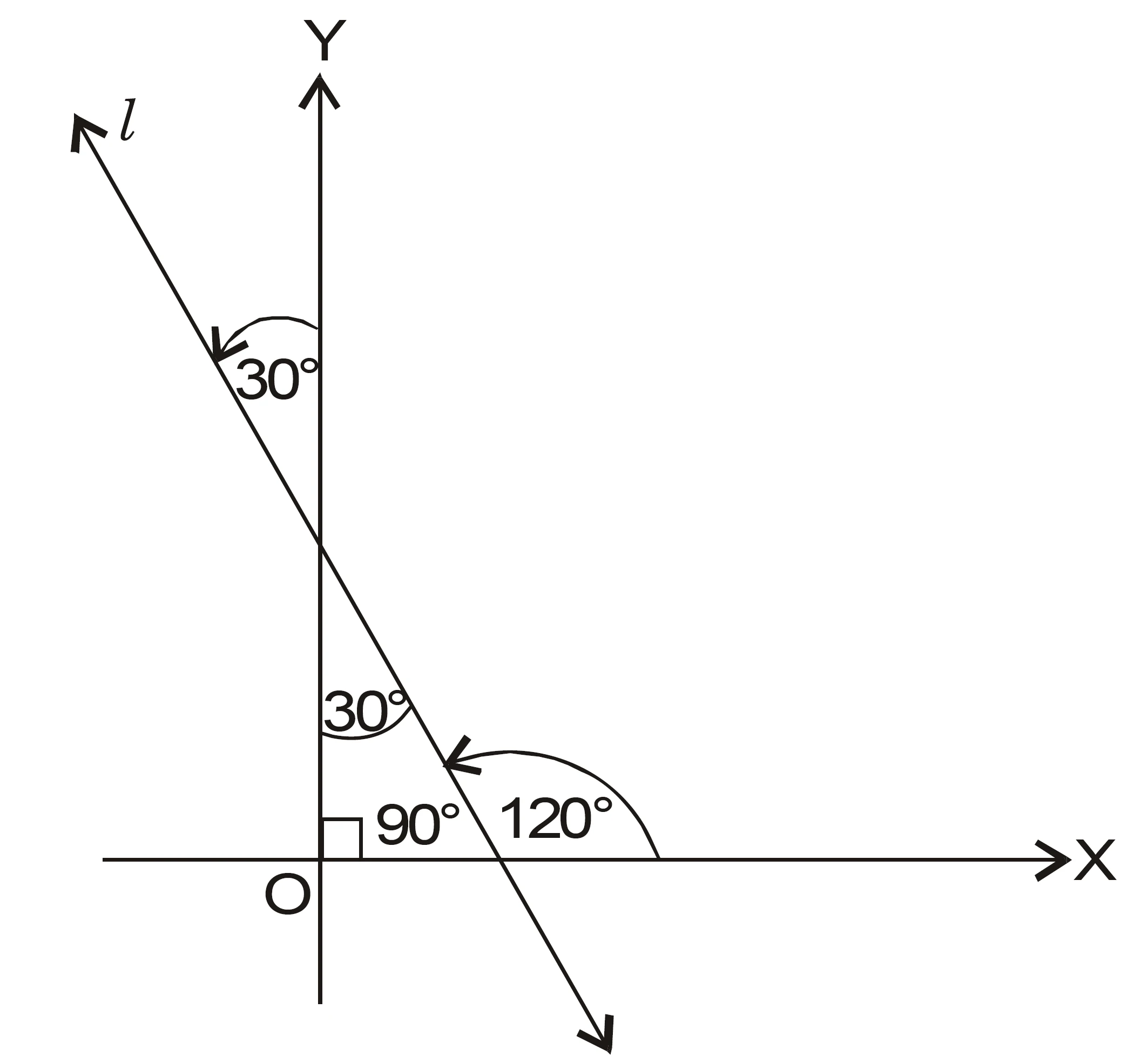
If a line makes an angle of $30^circ$ with the positive direction of the y-axis measured anticlockwise, then the angle made by the line with the positive direction of the x-axis (measured anticlockwise) is
$$
90^\circ + 30^\circ = 120^\circ
$$
∴ The slope of the given line is
$$
m = \tan(120^\circ)
$$
Now,
$$
\tan(120^\circ) = \tan(180^\circ – 60^\circ) = -\tan(60^\circ) = -\sqrt{3}
$$
Hence, the slope of the line m is $\boxed{-\sqrt{3}}$
NCERT Question.8 : Without using the distance formula, show that the points $(-2, -1)$, $(4, 0)$, $(3, 3)$, and $(-3, 2)$ are the vertices of a parallelogram.
Solution :
Let the given points be
$A(4, 0)$, $B(3, 3)$, $C(-3, 2)$, and $D(-2, -1)$.
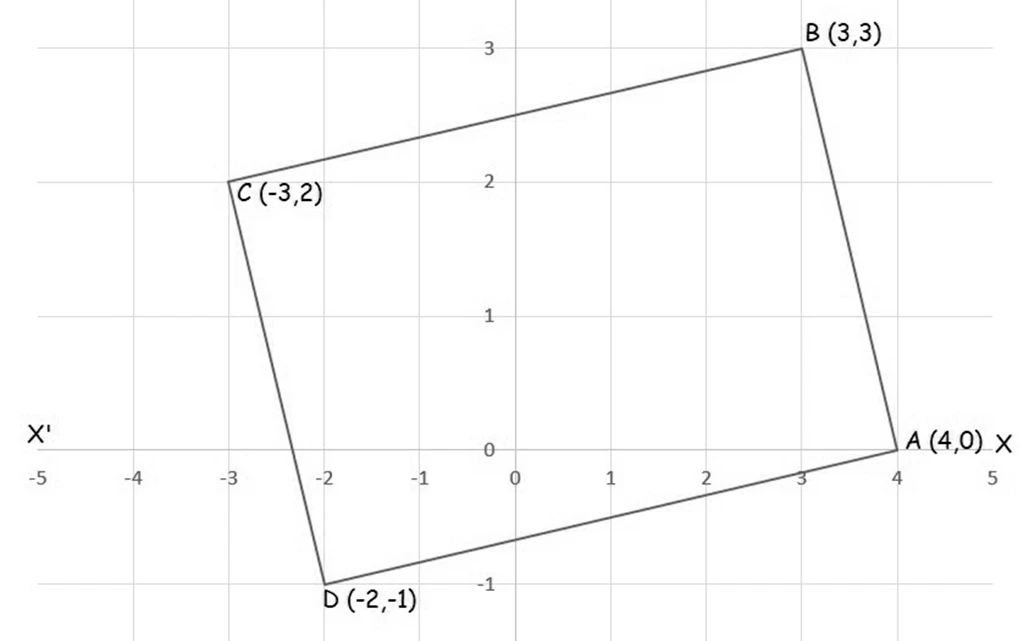
Slope of AD:
$$
m_{AD} = \frac{0 – (-1)}{4 – (-2)} = \frac{1}{6}
$$
Slope of BC:
$$
m_{BC} = \frac{3 – 2}{3 – (-3)} = \frac{1}{6}
$$
Hence,
$$
m_{AD} = m_{BC}
$$
∴ $AD \parallel BC$ ……………………..(1)
Slope of AB:
$$
m_{AB} = \frac{3 – 0}{3 – 4} = \frac{3}{-1} = -3
$$
Slope of CD:
$$
m_{CD} = \frac{2 – (-1)}{-3 – (-2)} = \frac{3}{-1} = -3
$$
Hence,
$$
m_{AB} = m_{CD}
$$
∴ $AB \parallel CD$ ……………………..(2)
From (1) and (2), both pairs of opposite sides are parallel.
∴ The quadrilateral $ABCD$ is a parallelogram.
Hence, the given vertices
$A(4, 0)$, $B(3, 3)$, $C(-3, 2)$, and $D(-2, -1)$
are the vertices of a parallelogram.
NCERT Question.9 : Find the angle between the $x$-axis and the line joining the points $(3, -1)$ and $(4, -2)$.
Solution :
The slope $m$ of the line passing through $(x_1, y_1)$ and $(x_2, y_2)$ is given by
$$
m = \frac{y_2 – y_1}{x_2 – x_1}, \quad \text{where } x_2 \ne x_1
$$
For the points $(3, -1)$ and $(4, -2)$:
$$
m = \frac{-2 – (-1)}{4 – 3}
$$
$$
m = \frac{-2 + 1}{1} = -1
$$
Since $m = \tan\theta$,
$$
\tan\theta = -1
$$
For a negative slope, the line makes an obtuse angle with the positive direction of the x-axis.
Thus,
$$
\theta = 180^\circ – 45^\circ = 135^\circ
$$
Hence, the angle between the x-axis and the line joining the points $(3, -1)$ and $(4, -2)$ is
$$
\boxed{135^\circ}
$$
NCERT Question.10 : The slope of a line is double the slope of another line. If the tangent of the angle between them is $\frac{1}{3}$, find the slopes of the lines.
Solution :
Let the slopes of the two lines be $m_1$ and $m_2$ such that
$$
m_1 = 2m_2 = 2m
$$
and
$$
\tan\theta = \frac{1}{3}
$$
We know that if $\theta$ is the angle between two lines having slopes $m_1$ and $m_2$, then
$$
\tan\theta = \left| \frac{m_1 – m_2}{1 + m_1 m_2} \right|
$$
Substituting the values,
$$
\frac{1}{3} = \left| \frac{2m – m}{1 + 2m^2} \right|
$$
$$
\frac{1}{3} = \left| \frac{m}{1 + 2m^2} \right|
$$
This gives two possible cases.
Case 1:
$$
\frac{1}{3} = \frac{m}{1 + 2m^2}
$$
Cross-multiplying,
$$
1 + 2m^2 = 3m
$$
$$
2m^2 – 3m + 1 = 0
$$
Factoring,
$$
(2m – 1)(m – 1) = 0
$$
$$
m = 1 \quad \text{or} \quad m = \frac{1}{2}
$$
Case 2:
$$
\frac{1}{3} = -\frac{m}{1 + 2m^2}
$$
Cross-multiplying,
$$
1 + 2m^2 = -3m
$$
$$
2m^2 + 3m + 1 = 0
$$
Factoring,
$$
(2m + 1)(m + 1) = 0
$$
$$
m = -1 \quad \text{or} \quad m = -\frac{1}{2}
$$
Results:
Hence, the possible pairs of slopes $(m, 2m)$ are:
- $(1, 2)$
- $\left( \frac{1}{2}, 1 \right)$
- $(-1, -2)$
- $\left( -\frac{1}{2}, -1 \right)$
Therefore,
the possible slopes of the two lines are
$$
\boxed{(1, 2)}, \quad \boxed{(-1, -2)}, \quad \boxed{\left(\frac{1}{2}, 1\right)}, \quad \boxed{\left(-\frac{1}{2}, -1\right)}
$$
NCERT Question.11 : A line passes through $(x_1, y_1)$ and $(h, k)$. If the slope of the line is $m$, show that $$ k – y_1 = m (h – x_1) $$
Solution :
We are given that the slope of the line is $m$.
The slope of a line passing through two points $(x_1, y_1)$ and $(h, k)$ is given by
$$
m = \frac{k – y_1}{h – x_1}
$$
Multiplying both sides by $(h – x_1)$, we get
$$
k – y_1 = m (h – x_1)
$$
Hence,
$$
\boxed{k – y_1 = m (h – x_1)}
$$
is proved.


