Anand Classes brings you comprehensive NCERT Solutions for Linear Programming Exercise 12.1 of Class 12 Chapter 12, offering step-by-step explanations and well-structured examples to improve conceptual clarity and exam performance. These high-quality notes simplify graphical methods and real-life optimization problems for effortless learning. Click the print button to download study material and notes.
Access NCERT Solutions Linear Programming Exercise 12.1 Class 12 Math Chapter-12
NCERT Question.6 : Minimise $$Z=x+2y$$ subject to $$2x+y\ge 3, \; x+2y\ge 6, \; x\ge 0,\quad y\ge 0$$
Solution
The feasible region lies in the first quadrant because $x\ge 0$ and $y\ge 0$.
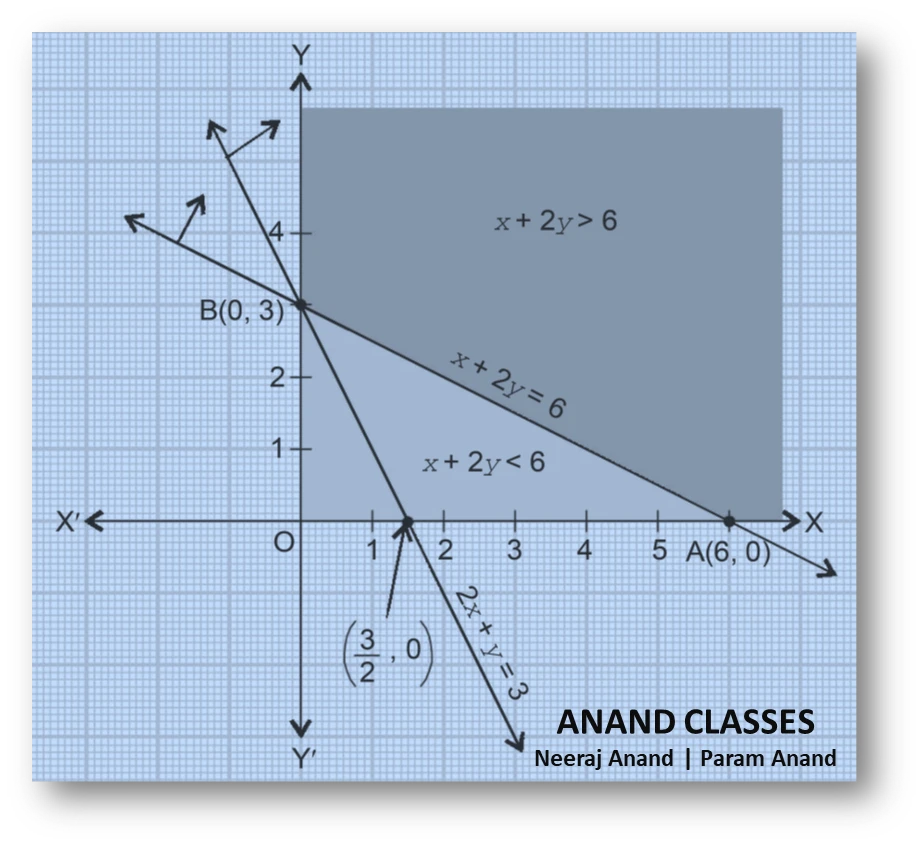
Tables of intercepts for the boundary lines
For the line $2x+y=3$:
| $x$ | $0$ | $ \dfrac{3}{2} $ |
|---|---|---|
| $y$ | $3$ | $0$ |
So the line joins points $(0,3)$ and $\left(\dfrac{3}{2},0\right)$.
For the line $x+2y=6$:
| $x$ | $0$ | $6$ |
|---|---|---|
| $y$ | $3$ | $0$ |
So the line joins points $(0,3)$ and $(6,0)$.
Testing the origin $(0,0)$:
- $2x+y\ge 3$ gives $0\not\ge 3$ false.
- $x+2y\ge 6$ gives $0\not\ge 6$ false.
Thus the feasible region lies away from the origin, on the opposite side of both lines.
The corner points of the feasible region are:
$$A=(6,0),\qquad B=(0,3).$$
Evaluate $Z=x+2y\;$ at corner points
| Corner point | Coordinates | $Z=x+2y$ |
|---|---|---|
| $A$ | $(6,0)$ | $6$ |
| $B$ | $(0,3)$ | $6$ |
Both corner points give the same value $Z=6$.
Consider any other point on the line $x+2y=6$.
For example, at $(2,2)$:
$$Z=2+2\cdot 2=6.$$
So every point on the boundary line $x+2y=6$ produces the same value $Z=6$.
Check the result :
Extend the solution by testing the half-plane $Z<m$, i.e. $x+2y<6$.
Graph of the inequality $x+2y<6$ (table of points for the boundary line)
For the line $x+2y=6$ take convenient points:
| $x$ | $0$ | $2$ | $6$ |
|---|---|---|---|
| $y$ | $3$ | $2$ | $0$ |
So the dotted line joining the points $,(0,3),(2,2),(6,0),$ represents the boundary $x+2y=6$. The line is drawn dotted because the inequality is strict ($<$), so the boundary itself is excluded.
Which side of the dotted line is $x+2y<6$?
Test the origin $(0,0)$ in $x+2y<6$:
$$x+2y=0<6\quad\text{(true)}.$$
Therefore the open half-plane defined by $x+2y<6$ is the side containing the origin.
Does the half-plane $x+2y<6$ meet the feasible region?
Recall the feasible region is determined by
$$2x+y\ge 3,\qquad x+2y\ge 6,\qquad x\ge 0,\qquad y\ge 0,$$
and the segment $AB$ (with $A=(6,0)$ and $B=(0,3)$) lies on the line $x+2y=6$ and is part of the feasible region. Points on the open half-plane $x+2y<6$ lie on the origin side of the dotted line, whereas the feasible region (including segment $AB$) lies on the opposite side or on the boundary.
Since every feasible point satisfies $x+2y\ge 6$, no feasible point can satisfy $x+2y<6$. Equivalently, the open half-plane $x+2y<6$ has no point in common with the feasible region.
Conclusion
Because the open half-plane $x+2y<6$ does not intersect the feasible region and the boundary line $x+2y=6$ is attained by feasible points, the minimum possible value $m$ of $Z=x+2y$ is $6$. Moreover this minimum is attained not only at the corner points $A=(6,0)$ and $B=(0,3)$ but at every point on the line segment $AB$ (for example $(2,2)$, $(3,1.5)$, etc.), since each such point satisfies $x+2y=6$ and the other constraints.
Final Result
$$\boxed{\;\displaystyle Z_{\min}=6\quad\text{attained at every point $\\[1em]$ on the segment} {(x,y):x+2y=6,0\le x\le 6\;}}$$
Download complete NCERT solution sets from Anand Classes for clear linear programming explanations with tables, dotted-line sketches, and many worked examples — ideal for JEE and CBSE exam practice and quick revision.
Final Result
$$\boxed{\displaystyle Z_{\min}=6\quad\text{for every point on the line}; x+2y=6}$$
Access detailed NCERT notes and linear programming explanations from Anand Classes — ideal for JEE and CBSE preparation with clear tables, solved examples, and step-by-step reasoning.
NCERT Question.7 : Maximise and Minimise $$Z=5x+10y$$ subject to $$x+2y\le 120, \; x+y\ge 60, \; x\ge 0,\quad y\ge 0$$
Solution
Feasible region lies in the first quadrant and is the intersection of the half-plane below the line $x+2y=120$ and the half-plane above the line $x+y=60$.
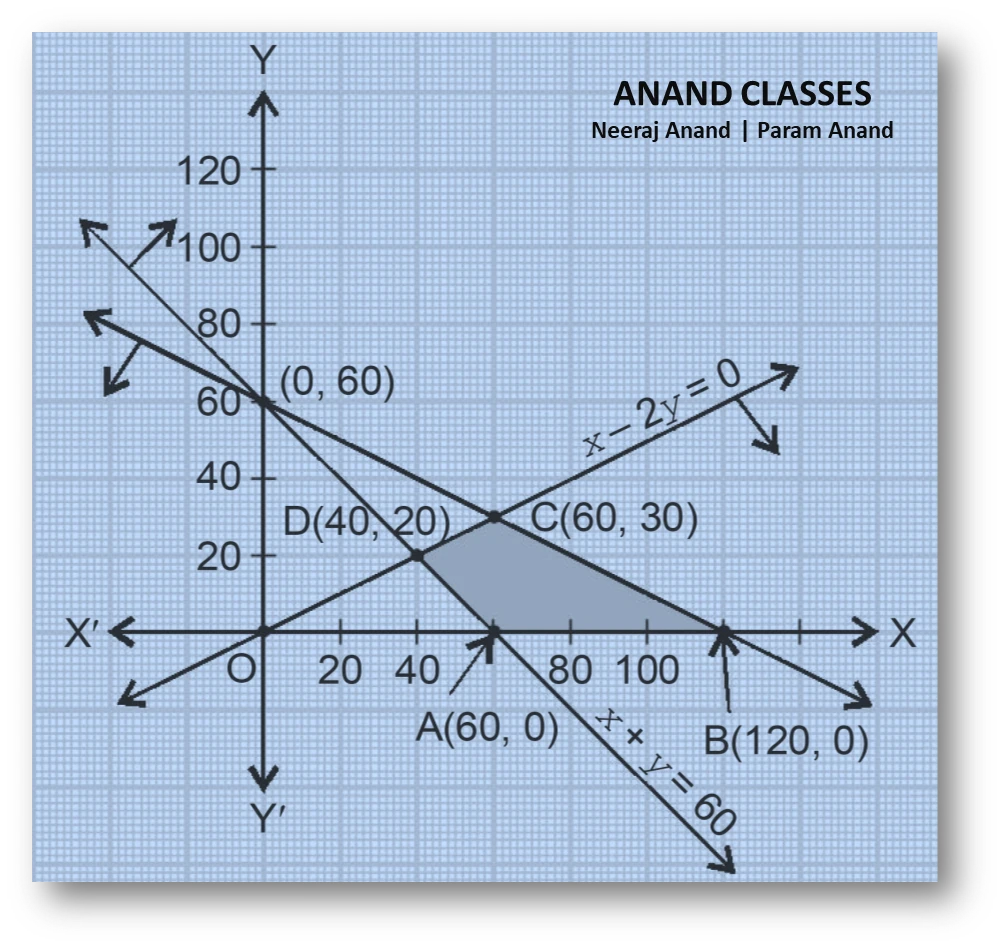
Boundary lines — intercepts (tables of points)
For the line $x+2y=120$:
| $x$ | $0$ | $120$ |
|---|---|---|
| $y$ | $60$ | $0$ |
So the line joins $(0,60)$ and $(120,0)$.
For the line $x+y=60$:
| $x$ | $0$ | $60$ |
|---|---|---|
| $y$ | $60$ | $0$ |
So the line joins $(0,60)$ and $(60,0)$.
The feasible region is therefore the triangle with vertices at
$$A=(60,0),\qquad B=(120,0),\qquad E=(0,60).$$
(Points such as $C=(60,30)$ and $D=(40,20)$ mentioned earlier lie on the edge between $B$ and $E$ or on the line $x+y=60$ respectively, and will be considered below.)
Evaluate $Z=5x+10y$ at the corner points
| Corner point | Coordinates | $Z=5x+10y$ |
|---|---|---|
| $A$ | $(60,0)$ | $5\cdot 60+10\cdot0=300$ |
| $B$ | $(120,0)$ | $5\cdot120+10\cdot0=600$ |
| $E$ | $(0,60)$ | $5\cdot0+10\cdot60=600$ |
So among the vertices, the smallest value is $300$ at $A=(60,0)$ and the largest value is $600$ (attained at $B$ and $E$).
Why the maximum is attained on the whole segment $BE$
Take any point on the boundary line $x+2y=120$. Parametrize it by $x=120-2y$ and substitute into $Z$:
$$Z=5(120-2y)+10y=600-10y+10y=600.$$
Hence $Z$ is identically $600$ for every point on the line $x+2y=120$. The portion of that line which lies inside the feasible region runs from $B=(120,0)$ to $E=(0,60)$, so every point on the segment $BE$ gives the maximum $Z=600$.
Summary table of some notable points (including interior/edge points)
| Point | Equation location | $Z=5x+10y$ |
|---|---|---|
| $A$ | $(60,0)$ vertex on $x+y=60$ | $300$ (minimum) |
| $D$ | $(40,20)$ on $x+y=60$ | $5\cdot40+10\cdot20=400$ |
| $C$ | $(60,30)$ on $x+2y=120$ | $600$ (on max segment) |
| Any point on $BE$ | $x+2y=120,0\le y\le60$ | $600$ (maximum) |
Final Results
$$\boxed{\;\displaystyle Z_{\min}=300\quad\text{at}\quad(60,0)\;}$$
$$\boxed{\;\displaystyle Z_{\max}=600\quad\text{attained at every point $\\[1em]$ on the segment} {(x,y):x+2y=120,0\le y\le 60\;}}$$
Get full solved NCERT linear programming sets and downloadable practice material from Anand Classes — concise step-by-step methods, clear tables, and worked examples ideal for JEE and CBSE preparation.
NCERT Question.8 : Minimise and Maximise $$Z=x+2y$$ subject to $$x+2y\ge 100, \; 2x-y\le 0, \; 2x+y\le 200, \;x\ge 0,\quad y\ge 0$$
Solution
Feasible region lies in the first quadrant because $(x\ge 0)$ and $(y\ge 0)$. We analyze each boundary line and its half-plane.
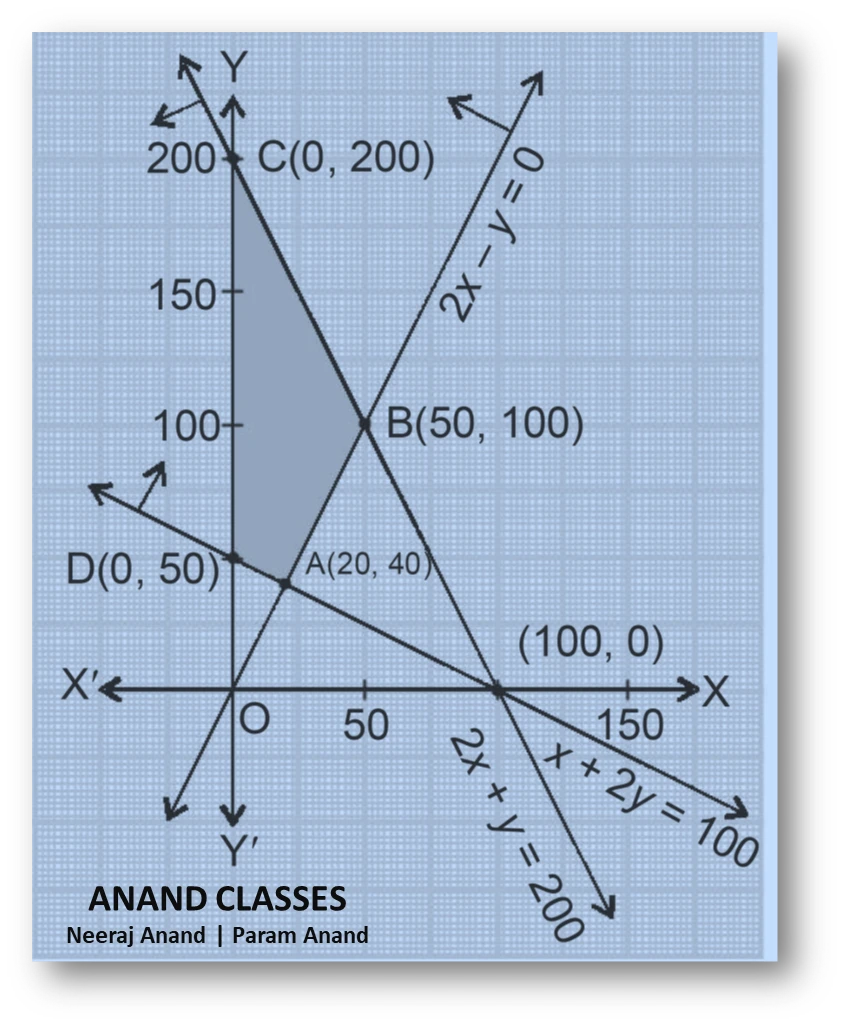
1. Line $(x+2y=100)$ (constraint $(x+2y\ge100)$)
Table of convenient points:
| (x) | (0) | (100) |
|---|---|---|
| (y) | (50) | (0) |
The line joins $(0,0)$ and $(100,0)$.
Test the origin $(0,0)$ in $(x+2y\ge100)$ : $(0\ge100)$ is false, so the feasible half-plane is the side away from the origin (the side that contains points with larger $(x+2y))$.
2. Line $(2x-y=0)$ (constraint $(2x-y\le0))$
Write as $(y=2x)$. Table:
| (x) | (0) | (20) |
|---|---|---|
| (y) | (0) | (40) |
The line passes through the origin.
Test the point $(100,0)$ in $(2x-y\le0)$: $(200\le0)$ is false, so the feasible half-plane is the side opposite to the side containing $(100,0)$. In other words, the feasible region satisfies $(y\ge 2x)$.
3. Line $(2x+y=200)$ (constraint $(2x+y\le200))$
Table:
| (x) | (0) | (100) |
|---|---|---|
| (y) | (200) | (0) |
The line joins $(0,200)$ and $(100,0)$.
Test the origin $(0,0)$ in $(2x+y\le200)$: $(0\le200)$ true, so the feasible half-plane is the origin side of this line.
The intersection of these half-planes with $(x,y\ge0)$ gives a bounded feasible polygon with vertices as found below.
Corner (extreme) points
Find intersections of the boundary lines:
Intersection of $(x+2y=100)$ and $(2x-y=0)$ (put ($y=2x)$):
$$
x+2(2x)=100\implies 5x=100\implies x=20, y=40.
$$
So $(A=(20,40))$.
Intersection of $(2x+y=200)$ and $(2x-y=0)$ (put $(y=2x)$):
$$
2x+2x=200\implies 4x=200\implies x=50, y=100.
$$
So $(B=(50,100))$.
Intercepts on the $(y)$-axis from the lines:
From $(2x+y=200)$ with $(x=0)$ gives $(C=(0,200))$.
From $(x+2y=100)$ with $(x=0)$ gives $(D=(0,50))$.
So the feasible polygon is $(A(20,40), B(50,100), C(0,200), D(0,50))$.
Evaluate $(Z=x+2y)$ at corner points
| Corner point | Coordinates | $(Z=x+2y)$ |
|---|---|---|
| $A$ | $(20,40)$ | $(20+2\cdot40=100)$ |
| $B$ | $(50,100)$ | $(50+2\cdot100=250)$ |
| $C$ | $(0,200)$ | $(0+2\cdot200=400)$ |
| $D$ | $(0,50)$ | $(0+2\cdot50=100)$ |
- Minimum among corner values: $(100)$ (attained at $(A)$ and $(D)$).
- Maximum among corner values: $(400)$ (attained at $(C)$).
Why the minimum occurs on the whole segment (AD)
The line $(x+2y=100)$ is exactly the boundary where $(Z=100)$. Every point of the segment joining $(A(20,40))$ and $(D(0,50))$ satisfies $(x+2y=100)$ and also satisfies the other constraints (in particular $(y\ge2x)$ and $(2x+y\le200))$, so $(Z=100)$ for every point on that segment. Thus the minimum is not unique but occurs on the entire segment $(AD)$.
Final Results
$$\boxed{\displaystyle Z_{\min}=100\quad\text{attained at every point $\\[1em]$ on the segment}{(x,y):x+2y=100,0\le x\le20}}$$
$$\boxed{\displaystyle Z_{\max}=400\quad\text{attained at}(0,200)}$$
Find more complete NCERT solution sets and downloadable practice material from Anand Classes — clear step-by-step linear programming methods, tables of intercepts, and worked examples ideal for JEE and CBSE preparation.
NCERT Question.9 : Maximise $$Z = -x + 2y$$ Subject to constraints: $$x \ge 3, \; x + y \ge 5, \; x + 2y \ge 6, \;y \ge 0$$
Solution
We have to Maximise
$$Z = -x + 2y$$
Subject to constraints:
$$x \ge 3, \; x + y \ge 5, \; x + 2y \ge 6, \;y \ge 0$$
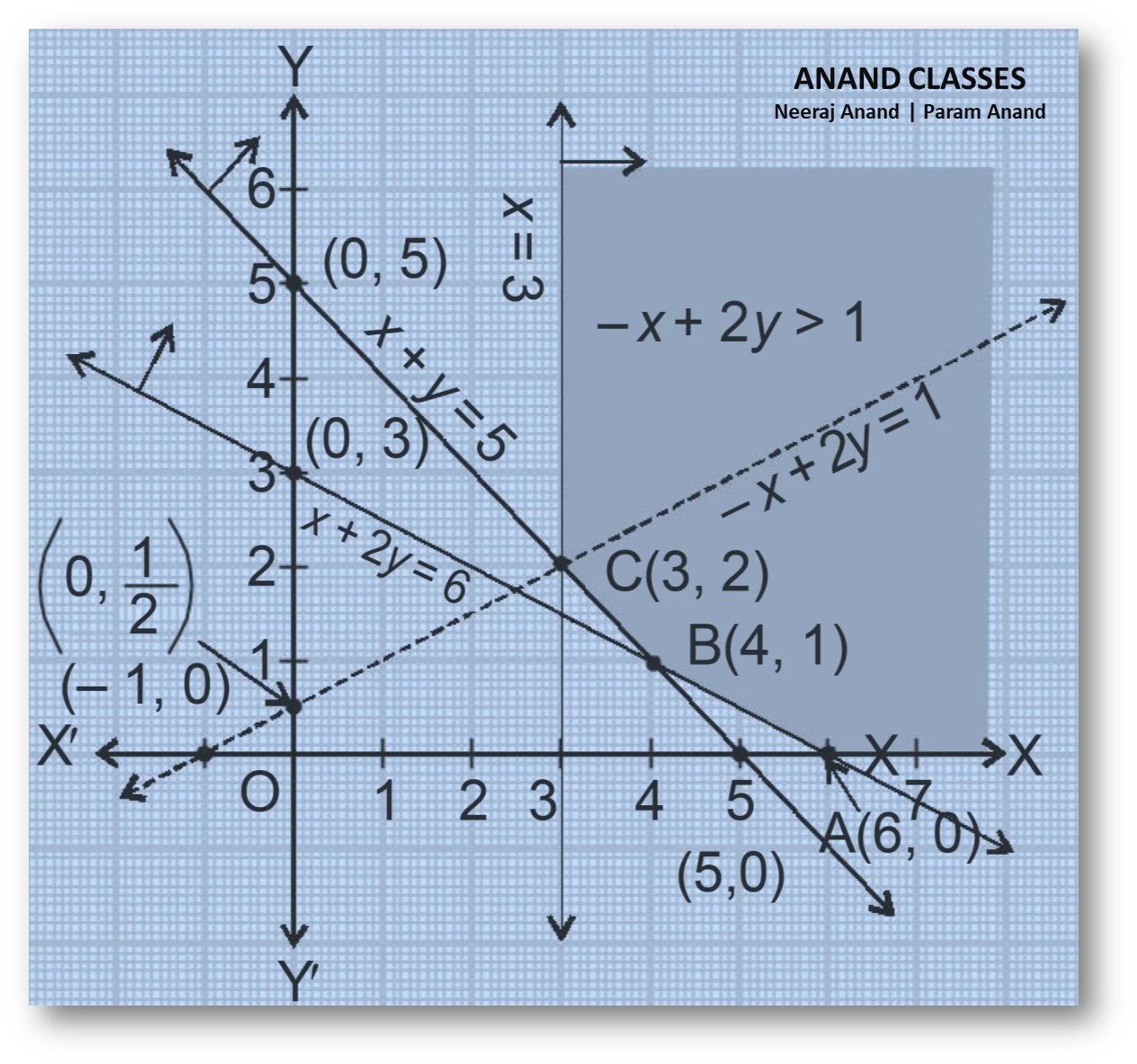
Step I : Plotting the Feasible Region
From constraint $y \ge 0$, the region lies above the x-axis.
From $x \ge 3$, the region lies right side of the vertical line $x = 3$.
For Line $x + y = 5$
| $x$ | $0$ | $5$ |
|---|---|---|
| $y$ | $5$ | $0$ |
So points: $(0,5)$ and $(5,0)$
Test origin $(0,0)$:
$$0 + 0 \ge 5 \Rightarrow 0 \ge 5 \ (\text{False})$$
So region does not include origin → opposite side of line.
For Line $x + 2y = 6$
| $x$ | $0$ | $6$ |
|---|---|---|
| $y$ | $3$ | $0$ |
So points: $(0,3)$ and $(6,0)$
Test origin $(0,0)$:
$$0 + 0 \ge 6 \Rightarrow 0 \ge 6 \ (\text{False})$$
So region is again non-origin side.
The feasible region is unbounded as per graph.
Step II : Find Corner Points
Point A is intersection of $x + 2y = 6$ with x-axis ⇒ Put $y=0$
$$x + 2(0) = 6 \Rightarrow x = 6$$
So $A(6,0)$
Point B is intersection of
$$x + y = 5$$
$$x + 2y = 6$$
Subtract the first from the second:
$$(x+2y)-(x+y)=6-5$$
$$y = 1$$
Put $y=1$ in $x+y=5$:
$$x+1=5 \Rightarrow x=4$$
So $B(4,1)$
Point C is intersection of $x + y = 5$ and $x = 3$
Put $x=3$:
$$3 + y = 5 \Rightarrow y = 2$$
So $C(3,2)$
Step III : Evaluate $Z$ at Corner Points
| Corner Point | $Z = -x + 2y$ |
|---|---|
| $A(6,0)$ | $-6$ |
| $B(4,1)$ | $-4 + 2 = -2$ |
| $C(3,2)$ | $-3 + 4 = 1$ (Maximum so far) |
So maximum candidate value is:
$$Z_{\max} = 1 \text{ at } (3,2)$$
Step IV : Check for Unbounded Region
Since region is unbounded, we must check if $1$ is actually the maximum.
Graph the inequality:
$$-x + 2y > 1$$
or
$$-x + 2y = 1$$
| $x$ | $0$ | $-1$ |
|---|---|---|
| $y$ | $\frac{1}{2}$ | $0$ |
So line passes through $\left(0,\frac{1}{2}\right)$ and $(-1,0)$ (dotted line)
Testing feasible region side → It keeps extending into region where $Z > 1$.
Thus:
Conclusion
There is no maximum value of $Z$ because the feasible region is unbounded in direction of increasing $Z$.
Final Result
✔ No maximum value exists for $Z = -x + 2y$ under given constraints.
Linear Programming solutions like this one are essential for CBSE Class 12, JEE Main preparation and competitive exams. Continue practicing more NCERT Maths Problems with detailed step-by-step graph-based explanations from Anand Classes to improve problem-solving confidence.
NCERT Question.10 : Maximise $$Z = x + y$$ Subject to $$x – y \le -1, \; -x + y \le 0, \; x \ge 0,\quad y \ge 0$$
Solution
We have to maximise
$$Z = x + y$$
subject to the constraints:
$$x – y \le -1, \; -x + y \le 0, \; x \ge 0,\quad y \ge 0$$

Step I — Plotting the constraints and determining half-planes
From constraints $$x \ge 0$$ and $$y \ge 0$$ the feasible region (if any) must lie in the first quadrant.
Line for $$x – y = -1$$ (constraint (1))
Table of convenient points:
| $x$ | $0$ | $-1$ |
|---|---|---|
| $y$ | $1$ | $0$ |
So the line joins $(0,1)$ and $(-1,0)$. Test the origin $(0,0)$ in $$x – y \le -1$$:
$$0 – 0 \le -1\quad\text{gives}\quad 0 \le -1\quad(\text{false}).$$
Therefore the feasible half-plane for this constraint is the side away from the origin (the side where $x-y$ is smaller than or equal to $-1$).
Line for $$-x + y = 0$$ i.e. $$y = x$$ (constraint (2))
Table of convenient points:
| $x$ | $0$ | $2$ |
|---|---|---|
| $y$ | $0$ | $2$ |
So the line joins $(0,0)$ and $(2,2)$. Test the point $(2,0)$ (not the origin) in $$-x + y \le 0$$:
$$-2 + 0 \le 0\quad\text{gives}\quad -2 \le 0\quad(\text{true}).$$
So the feasible half-plane for this constraint is the side containing $(2,0)$, i.e. the side where $y \le x$.
Step II — Check intersection of half-planes
Constraint (1) requires points with $x – y \le -1$ which can be rewritten as $y \ge x + 1,$ (moving $y$ to left and constants).
Constraint (2) requires $y \le x$.
Combine these two: for any point to satisfy both we would need
$$x + 1 \le y \le x.$$
That inequality chain simplifies to
$$x + 1 \le x,$$
which is impossible for any real $x$ (since $x+1>x$ always). Hence there is no point that simultaneously satisfies both $$y \ge x + 1$$ and $$y \le x$$.
Because the half-planes determined by constraints (1) and (2) do not overlap, and together with $$x\ge0$$ and $$y\ge0$$ there is no common point, the system has no feasible region.
Conclusion
There is no feasible solution to the given system of constraints. Therefore the optimisation problem has no maximum value (and no meaningful minimum in the feasible-sense) because the feasible set is empty.
Final Statement
$$\boxed{\text{No feasible region exists, hence no maximum value of }Z = x + y.}$$
Find concise, fully worked NCERT solutions and downloadable practice sets from Anand Classes — perfect for CBSE and competitive exam preparation with clear step-by-step reasoning and handy tables.


