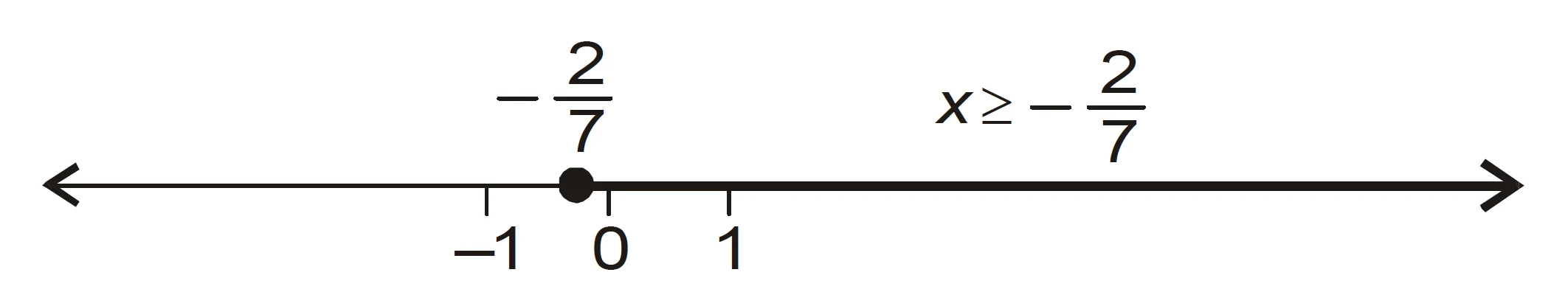Anand Classes offers comprehensive and well-structured NCERT Solutions for Linear Inequalities Exercise 5.1 Class 11 Maths Chapter 5 (Set-2) to help students build a clear understanding of linear inequalities. These step-by-step solutions strictly follow the latest NCERT and CBSE syllabus, ensuring accuracy and conceptual clarity. Designed to make exam preparation easy, these solutions cover all important types of questions from the chapter, enabling Class 11 students to strengthen their problem-solving skills. Click the print button to download study material and notes.
NCERT Question 11. Solve $\dfrac{3(x – 2)}{5} \le \dfrac{5(2 – x)}{3}$ for real $x$
Solution:
Given,
$$\frac{3(x – 2)}{5} \le \frac{5(2 – x)}{3}$$
Now by cross – multiplying the denominators, we get
$$9(x – 2) \le 25(2 – x)$$
$$9x – 18 \le 50 – 25x$$
Now let us add $25x$ both the sides,
$$9x – 18 + 25x \le 50 – 25x + 25x$$
$$34x – 18 \le 50$$
Let us add $18$ both the sides,
$$34x – 18 + 18 \le 50 + 18$$
$$34x \le 68$$
Dividing both the sides by $34$,
$$\frac{34x}{34} \le \frac{68}{34}$$
$$x \le 2$$
Thus, the solution of the given equation is defined by all the real numbers less than or equal to $2$.
Hence, solution set is $$(-infty,, 2]$$
NCERT Question 12. Solve $ \dfrac{1}{2}\left(\dfrac{3x}{5} + 4\right) \ge \dfrac{1}{3}(x – 6) )$ for real $x$
Solution:
Given,
$$\frac{1}{2}\left(\frac{3x}{5} + 4\right) \ge \frac{1}{3}(x – 6)$$
Now let us cross-multiply,
$$3\left(\frac{3x}{5} + 4\right) \ge 2(x – 6)$$
Now multiply the respective terms at both sides,
$$\frac{9x}{5} + 12 \ge 2x – 12$$
Now subtracting $12$ from both the sides,
$$\frac{9x}{5} + 12 – 12 \ge 2x – 12 – 12$$
$$\frac{9x}{5} \ge 2x – 24$$
Now multiplying by $5$ both the sides,
$$9x \ge 10x – 120$$
Now subtracting $10x$ from both the sides,
$$-x \ge -120$$
Now multiplying with $-1$ both the sides (reversing the inequality sign),
$$x \le 120$$
Thus, the solutions of the given equation are defined by all the real numbers less than or equal to $120$.
Hence, the required solution set is:
$$(-\infty, 120]$$
NCERT Question 13. Solve (2(2x + 3) – 10 < 6(x – 2)) for real $x$
Solution:
Given,
$$2(2x + 3) – 10 < 6(x – 2)$$
By multiplying we get,
$$4x + 6 – 10 < 6x – 12$$
On simplifying,
$$4x – 4 < 6x – 12$$
Now bring like terms together,
$$4x – 6x < -12 + 4$$
$$-2x < -8$$
Now divide both sides by (-2).
When dividing or multiplying both sides of an inequality by a negative number, the inequality sign reverses:
$$x > 4$$
Thus, the solution of the given inequality consists of all real numbers greater than (4).
Hence, the required solution set is:
$$(4, \infty)$$
Boost your algebra skills with high-quality study materials from Anand Classes — perfect for CBSE Class 11 maths.
NCERT Question 14. Solve $(37 – (3x + 5) \ge 9x – 8(x – 3))$ for real $x$
Solution:
Given,
$$37 – (3x + 5) \ge 9x – 8(x – 3)$$
On simplifying,
$$37 – 3x – 5 \ge 9x – 8x + 24$$
$$32 – 3x \ge x + 24$$
Rearranging the terms,
$$32 – 24 \ge x + 3x$$
$$8 \ge 4x$$
Dividing both sides by (4),
$$2 \ge x$$
or
$$x \le 2$$
Thus, all real numbers less than or equal to (2) satisfy the inequality.
Hence, the required solution set is:
$$(-\infty 2]$$
Score high in inequalities with Anand Classes — your trusted support for CBSE and competitive exam mathematics.
NCERT Question 15. Solve $\dfrac{x}{4} < \dfrac{5x – 2}{3} – \dfrac{7x – 3}{5}$ for real $x$
Solution:
Given,
$$\frac{x}{4} < \frac{5x – 2}{3} – \frac{7x – 3}{5}$$
Take (15) as the LCM on the right-hand side:
$$\frac{x}{4} < \frac{5(5x – 2) – 3(7x – 3)}{15}$$
Simplifying,
$$\frac{x}{4} < \frac{(25x – 10) – (21x – 9)}{15}$$
Multiply both sides by (15):
$$\frac{15x}{4} < 25x – 10 – 21x + 9$$
$$\frac{15x}{4} < 4x – 1$$
Multiply both sides by (4):
$$15x < 16x – 4$$
Rearranging,
$$4 < x$$
or
$$x > 4$$
Thus, all real numbers greater than (4) satisfy the inequality.
Hence, the required solution set is:
$$(4, \infty)$$
Boost your confidence in algebra with Anand Classes, the perfect place for CBSE and competitive exam preparation!
NCERT Question 16. Solve $\displaystyle \frac{2x-1}{3} \ge \frac{3x-2}{4} – \frac{2-x}{5}$ for real $x$
Solution:
Given
$$\frac{2x-1}{3} \ge \frac{3x-2}{4} – \frac{2-x}{5}$$
Combine the right-hand side over common denominator (20):
$$\frac{3x-2}{4} – \frac{2-x}{5}=\frac{5(3x-2)-4(2-x)}{20}$$ $$ =\frac{15x-10-(8-4x)}{20}=\frac{19x-18}{20}$$
So the inequality becomes
$$\frac{2x-1}{3} \ge \frac{19x-18}{20}$$
Clear denominators by multiplying both sides by (60) (or equivalently multiply left by (20) and right by (3)):
$$20(2x-1) \ge 3(19x-18)$$
Expand:
$$40x-20 \ge 57x-54$$
Bring like terms together:
$$40x-57x \ge -54+20$$
$$-17x \ge -34$$
Divide by (-17) and reverse the inequality sign:
$$x \le 2$$
Final Answer
$$\boxed{(-\infty, 2]}$$
Boost your algebra practice with concise notes from Anand Classes — perfect for CBSE and competitive exam preparation.
NCERT Question 17. Solve the inequality $(3x – 2 < 2x + 1)$ and show the graph of the solution on number line.
Solution:
Given
$$3x – 2 < 2x + 1$$
Rearranging terms:
$$3x – 2x < 1 + 2$$
$$x < 3$$
Final Answer
$$\boxed{(-\infty, 3)}$$
The graphical representation of the solutions is given in the figure below.

Practice more linear inequality solutions with Anand Classes — ideal for CBSE and competitive exam success!
NCERT Question 18. Solve the inequality $(5x – 3 \ge 3x – 5)$ and show the graph of the solution on number line.
Solution:
Given
$$5x – 3 \ge 3x – 5$$
Rearranging terms:
$$5x – 3x \ge -5 + 3$$
$$2x \ge -2$$
Dividing both sides by (2):
$$x \ge -1$$
Final Answer
$$\boxed{[-1,\infty)}$$
The graphical representation of the solutions is given in the figure below.
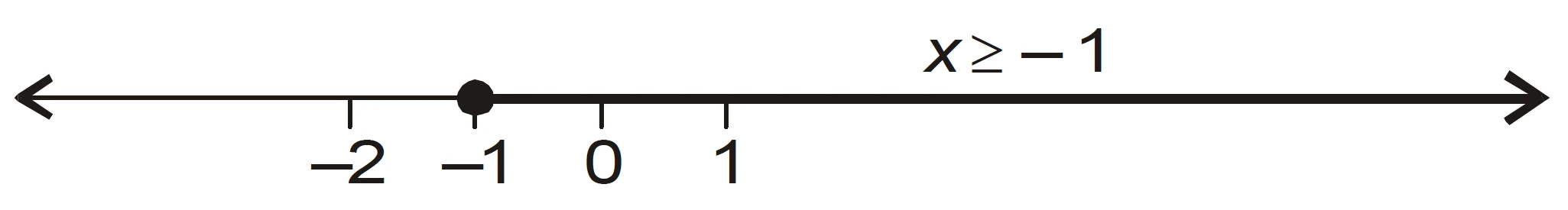
Strengthen your understanding of inequalities with Anand Classes — perfect for CBSE and competitive exams!
NCERT Question 19. Solve the inequality $(3(1 – x) < 2(x + 4))$ and show the graph of the solution on number line.
Solution:
Given
$$3(1 – x) < 2(x + 4)$$
Multiply:
$$3 – 3x < 2x + 8$$
Rearranging:
$$3 – 8 < 2x + 3x$$
$$-5 < 5x$$
Dividing both sides by (5):
$$-1 < x$$
Final Answer
$$\boxed{(-1,\infty)}$$
The graphical representation of the solutions is given in the figure below.
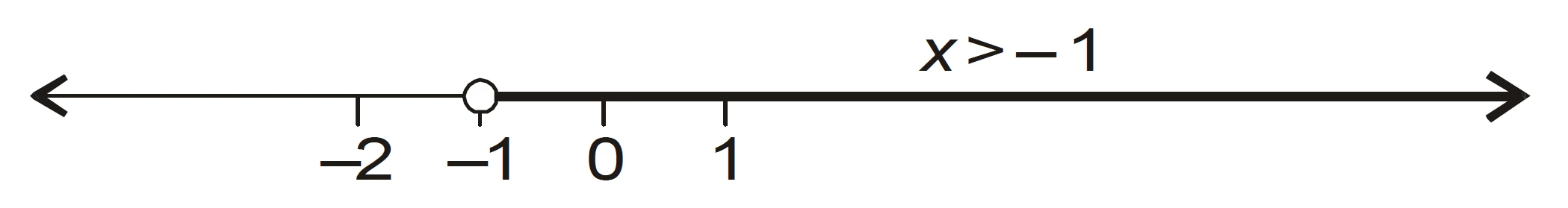
Build your inequality problem-solving skills with Anand Classes — ideal for CBSE and Olympiad preparation!
NCERT Question 20. Solve the inequality
$$\frac{x}{2} \ge \frac{5x – 2}{3} – \frac{7x – 3}{5}$$ and show the graph of the solution on number line.
Solution:
Simplify the right side:
Take LCM (15):
$$
\frac{x}{2} \ge \frac{5(5x – 2) – 3(7x – 3)}{15}
$$
Expand:
$$
\frac{x}{2} \ge \frac{25x – 10 – 21x + 9}{15}
$$
$$
\frac{x}{2} \ge \frac{4x – 1}{15}
$$
Cross multiply:
$$
15x \ge 2(4x – 1)
$$
$$
15x \ge 8x – 2
$$
$$
15x – 8x \ge -2
$$
$$
7x \ge -2
$$
Divide both sides by (7):
$$
x \ge -\frac{2}{7}
$$
Final Answer
$$
\boxed{x \in \left[-\frac{2}{7}, \infty\right)}
$$
The graphical representation of the solutions is given in the figure below.