Anand Classes provides comprehensive and easy-to-understand NCERT Solutions for Linear Programming Exercise 12.1 of Class 12 Chapter 12, designed to help students master the fundamentals of constraints, objective functions, and graphical methods. These detailed solutions simplify complex problem-solving steps and strengthen conceptual clarity, ensuring students score higher in board examinations. Click the print button to download study material and notes.
NCERT Question 1 : Maximise $$Z = 3x + 4y$$ subject to the constraints
$$x + y \le 4,\; x \ge 0, \;y \ge 0.$$
Solution
Feasible Region
The constraints
- $x \ge 0$
- $y \ge 0$
imply that the feasible region lies in the first quadrant.
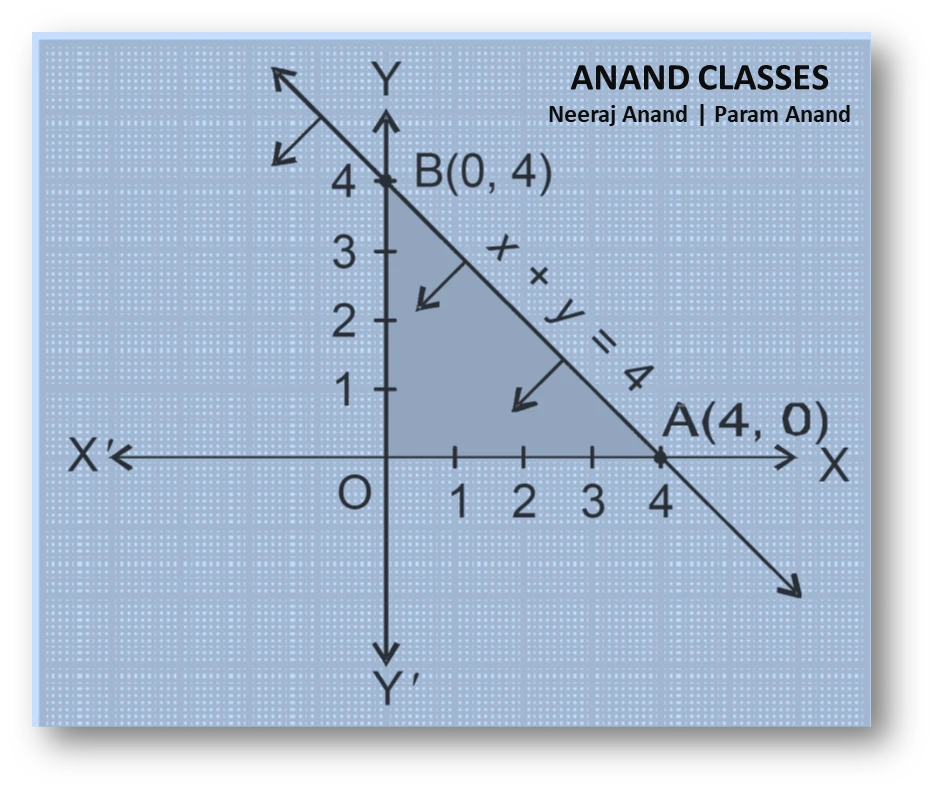
The main boundary line is:
$$x + y = 4.$$
Table of Values for the Line
To plot this line, use two convenient points:
| $x$ | $y$ |
|---|---|
| 0 | 4 |
| 4 | 0 |
Thus, we draw a straight line through points $(4, 0)$ and $(0, 4)$.
To determine the feasible side, test the origin $(0,0)$ in the inequality:
$$0 + 0 \le 4 \Rightarrow \text{True.}$$
Therefore, the region towards the origin is the feasible region.
The resulting feasible region is triangle OAB with corner points:
- $O(0,0)$
- $A(4,0)$
- $B(0,4)$
Evaluating the Objective Function
Compute $Z = 3x + 4y$ at each corner point:
| Corner Point | $Z = 3x + 4y$ |
|---|---|
| $O(0,0)$ | $0$ |
| $A(4,0)$ | $12$ |
| $B(0,4)$ | $16$ (Maximum) |
Final Result
The maximum value of
$$Z = 3x + 4y$$
is
$$\boxed{16}$$
which occurs at the point
$$\boxed{(0,4)}.$$
Enhance your conceptual clarity in Linear Programming with detailed NCERT-style explanations from Anand Classes — ideal for CBSE exams, JEE preparation, and strong mathematical foundations.
NCERT Question 2: Minimise $$Z=-3x+4y$$ subject to the constraints
$$x+2y\le 8,\;3x+2y\le 12,\;x\ge0,\;y\ge0$$
Solution
Feasible region lies in the first quadrant because $x\ge0$ and $y\ge0$. The two boundary lines are
$$x+2y=8$$
and
$$3x+2y=12.$$
Find intercepts to locate the lines and corner points.
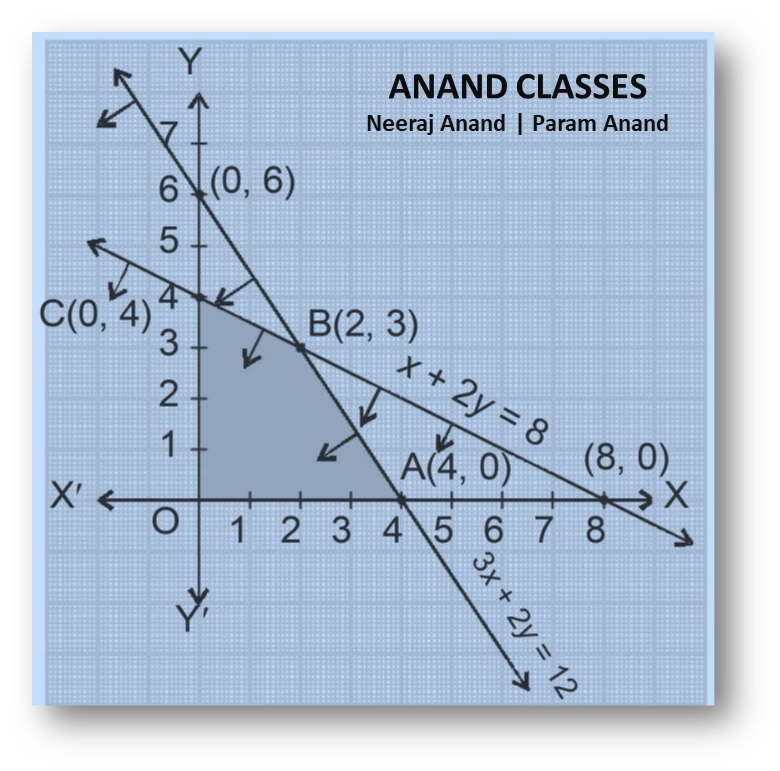
Table of intercepts for the line $x+2y=8$
| $x$ | $y$ |
|---|---|
| $0$ | $4$ |
| $8$ | $0$ |
So the line passes through $(0,4)$ and $(8,0)$ and the feasible side is toward the origin since $0+0\le8$.
Table of intercepts for the line $3x+2y=12$
| $x$ | $y$ |
|---|---|
| $0$ | $6$ |
| $4$ | $0$ |
So this line passes through $(0,6)$ and $(4,0)$ and the feasible side is toward the origin since $0+0\le12$.
Find intersection $B$ of the two lines by solving
$$\begin{cases}
x+2y=8\\
3x+2y=12
\end{cases}$$
Subtracting the first from the second gives $2x=4$, so $x=2$. Substitute back $2+2y=8\Rightarrow 2y=6\Rightarrow y=3$. Thus $B=(2,3)$.
The feasible polygon (bounded by axes and the two lines) has vertices
$$O(0,0), A(4,0), B(2,3), C(0,4).$$
Evaluate the objective function $Z=-3x+4y$ at each vertex:
| Vertex | Coordinates $(x,y)$ | $Z=-3x+4y$ |
|---|---|---|
| $O$ | $(0,0)$ | $0$ |
| $A$ | $(4,0)$ | $-12$ (Minimum) |
| $B$ | $(2,3)$ | $-3(2)+4(3)=-6+12=6$ |
| $C$ | $(0,4)$ | $16$ |
Compare the values: $0,-12,6,16$. The minimum value is $-12$, attained at the vertex $A=(4,0)$.
Final answer: the minimum value is $$\boxed{Z_{\min}=-12\text{ at }(x,y)=(4,0)}.$$
For additional practice and concise NCERT-style solutions with clear step-by-step reasoning and worked corner-point tables, check out the study packets and downloadable notes from Anand Classes — ideal for CBSE exam prep and strengthening linear-programming skills.
NCERT Question 3: Maximise $$Z=5x+3y$$ subject to the constraints $$3x+5y\le 15,\;5x+2y\le 10,\;x\ge0,\;y\ge0$$
Solution
Feasible region lies in the first quadrant because $x\ge0$ and $y\ge0$.
The two boundary lines are
$$3x+5y=15$$ and $$5x+2y=10.$$
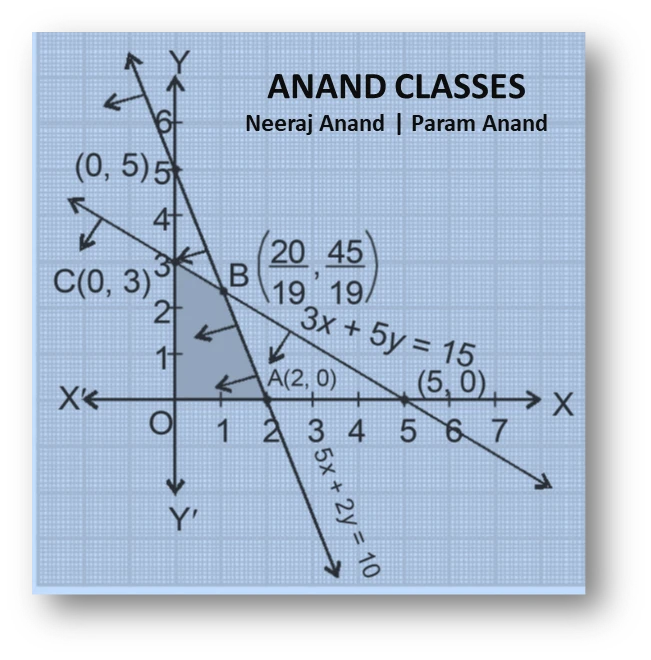
Find intercepts to locate the lines and corner points.
Table of intercepts for the line $3x+5y=15$
| $x$ | $y$ |
|---|---|
| $0$ | $3$ |
| $5$ | $0$ |
So the line passes through $(0,3)$ and $(5,0)$.
Test the origin $(0,0)$: $0\le15$ is true, so the feasible side is toward the origin.
Table of intercepts for the line $5x+2y=10$
| $x$ | $y$ |
|---|---|
| $0$ | $5$ |
| $2$ | $0$ |
So this line passes through $(0,5)$ and $(2,0)$.
Test the origin: $0\le10$ is true, so the feasible side is toward the origin.
Find intersection $B$ of the two lines by solving
$$\begin{cases}
3x+5y=15\\
5x+2y=10
\end{cases}$$
Multiply the first equation by $2$: $6x+10y=30$. Multiply the second by $5$: $25x+10y=50$. Subtract the first from the second:
$$25x+10y -(6x+10y)=50-30\implies 19x=20\implies x=\frac{20}{19}.$$
Substitute into $5x+2y=10$:
$$2y=10-5x=10-\frac{100}{19}=\frac{190-100}{19}=\frac{90}{19}\implies y=\frac{45}{19}.$$
Thus $B=\left(\dfrac{20}{19},\dfrac{45}{19}\right)$.
The feasible polygon (bounded by axes and the two lines) has vertices
$$O(0,0),A(2,0),B\Big(\frac{20}{19},\frac{45}{19}\Big),C(0,3).$$
(Here $A(2,0)$ is where $5x+2y=10$ meets the $x$-axis, $C(0,3)$ is where $3x+5y=15$ meets the $y$-axis.)
Evaluate the objective function $Z=5x+3y$ at each vertex:
| Vertex | Coordinates $(x,y)$ | $Z=5x+3y$ |
|---|---|---|
| $O$ | $(0,0)$ | $0$ |
| $A$ | $(2,0)$ | $5(2)+3(0)=10$ |
| $B$ | $\left(\dfrac{20}{19},\dfrac{45}{19}\right)$ | $5\cdot\dfrac{20}{19}+3\cdot\dfrac{45}{19}=\dfrac{100+135}{19}=\dfrac{235}{19}$ (Maximum) |
| $C$ | $(0,3)$ | $5(0)+3(3)=9$ |
Compare the values $0,10,\dfrac{235}{19},9$. Note that
$$\dfrac{235}{19}=12+\dfrac{7}{19}\approx 12.3684$$
so the maximum value is $\dfrac{235}{19}$ attained at
$$\boxed{\left(x,y\right)=\left(\dfrac{20}{19},\dfrac{45}{19}\right)}.$$
Final answer: the maximum value is $$\boxed{Z_{\max}=\dfrac{235}{19}\text{ at }\left(\dfrac{20}{19},\dfrac{45}{19}\right).}$$
Practice more linear-programming problems with stepwise NCERT solutions from Anand Classes to build strong problem-solving skills.
NCERT Question.4 : Minimise $$Z=3x+5y$$ subject to $$x+3y\ge 3, \; x+y\ge 2, \; x\ge 0,\quad y\ge 0$$
Solution
Feasible region lies in the first quadrant because $x\ge0$ and $y\ge0$.
The two boundary lines are $x+3y=3$ and $x+y=2$ and the corresponding half-planes.
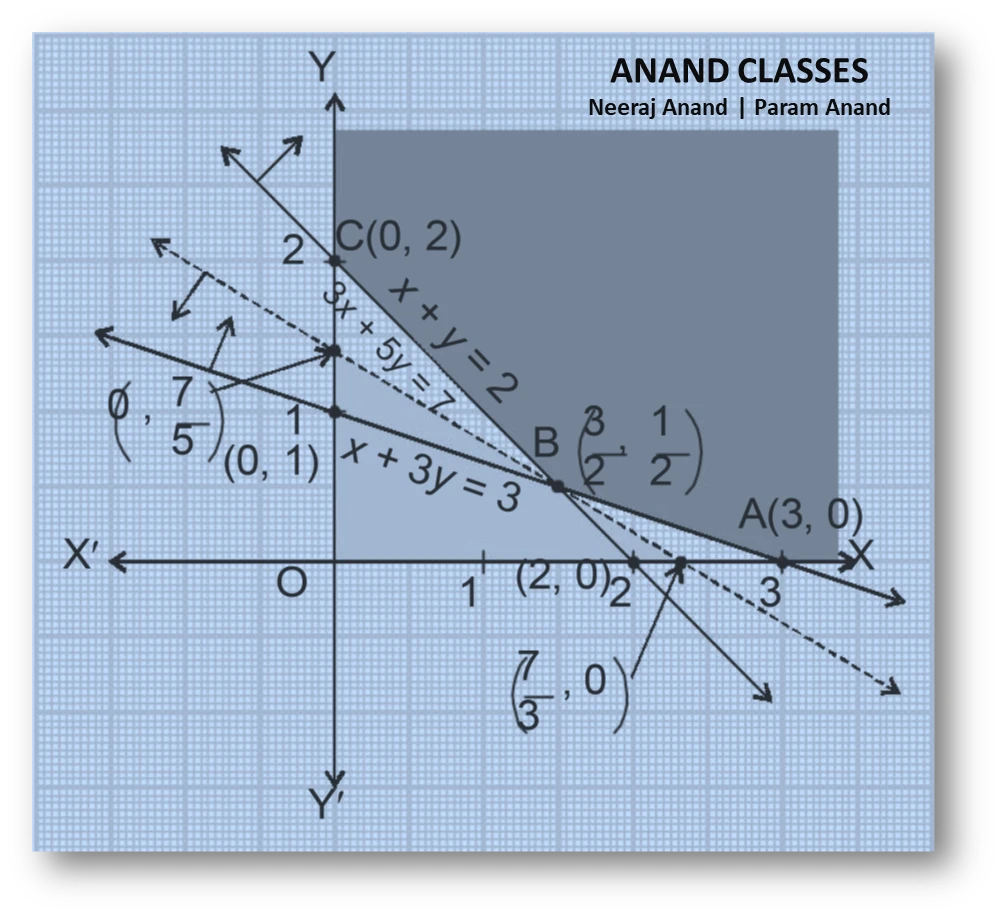
Intercepts (tables of points for the boundary lines)
For the line $x+3y=3$:
| $x$ | $0$ | $3$ |
|---|---|---|
| $y$ | $1$ | $0$ |
So the line joins points $(0,1)$ and $(3,0)$.
For the line $x+y=2$:
| $x$ | $0$ | $2$ |
|---|---|---|
| $y$ | $2$ | $0$ |
So the line joins points $(0,2)$ and $(2,0)$.
Testing a point (for example origin $(0,0)$) shows $0\not\ge 3$ and $0\not\ge 2$ so the feasible region is the intersection of the half-planes that lie away from the origin as determined by the inequalities. The feasible region is unbounded (it extends outward), and its corner (extreme) points visible are
$$A=(3,0),\quad B=\left(\frac{3}{2},\frac{1}{2}\right),\quad C=(0,2).$$
Find intersection point $B$ of the two lines
Solve
$$x+3y=3\quad\text{and}\quad x+y=2.$$
Subtract the second from the first:
$$2y=1\implies y=\frac{1}{2}.$$
Then $x=2-y=2-\dfrac{1}{2}=\dfrac{3}{2}.$
So $B=\left(\dfrac{3}{2},\dfrac{1}{2}\right)$.
Evaluate $Z=3x+5y$ at corner points
| Corner point | Coordinates | $Z=3x+5y$ |
|---|---|---|
| $A$ | $(3,0)$ | $3\cdot3+5\cdot0=9$ |
| $B$ | $\left(\dfrac{3}{2},\dfrac{1}{2}\right)$ | $3\cdot\dfrac{3}{2}+5\cdot\dfrac{1}{2}=\dfrac{9}{2}+\dfrac{5}{2}=7$ |
| $C$ | $(0,2)$ | $3\cdot0+5\cdot2=10$ |
So among the corner values, the smallest is $7$ at $B$.
Proof that $7$ is the global minimum
Add the two constraint inequalities with appropriate weights:
$$ (x+3y)+2(x+y)=3+4 $$
Since $x+3y\ge 3$ and $x+y\ge 2$, summing gives
$$3x+5y\ge 7$$
for every feasible point $(x,y)$. Hence $Z=3x+5y$ cannot be smaller than $7$ on the feasible region. Because point $B$ attains $Z=7$, it is the minimum.
Check : Extend the solution by testing the half-plane $Z<m$, i.e. $3x+5y<7$.
Graph of the inequality $3x+5y<7$ (table of points for the boundary line)
For the line $3x+5y=7$ we may take the points:
| $x$ | $0$ | $1$ | $\dfrac{7}{3}$ |
|---|---|---|---|
| $y$ | $\dfrac{7}{5}$ | $\dfrac{4}{5}$ | $0$ |
So the dotted line joining the points $\left(0,\dfrac{7}{5}\right)$, $\left(1,\dfrac{4}{5}\right)$ and $\left(\dfrac{7}{3},0\right)$ represents the boundary $3x+5y=7$. The line is drawn dotted because the inequality is strict ($<$), so the boundary itself is excluded.
Which side of the dotted line is $3x+5y<7$?
Test the origin $(0,0)$ in $3x+5y<7$:
$$3\cdot 0+5\cdot 0=0<7\quad\text{(true)}.$$
Therefore the half-plane defined by $3x+5y<7$ is the side containing the origin.
Does the half-plane $3x+5y<7$ meet the feasible region?
From the constraints we previously derived (by adding and weighting the given inequalities) we have, for every feasible point $(x,y)$,
$$3x+5y\ge 7.$$
Hence no feasible point can satisfy $3x+5y<7$. Equivalently, the entire feasible region lies on the opposite side of the dotted line (or on the boundary), and the open half-plane $3x+5y<7$ has no point in common with the feasible region.
Conclusion
Since no feasible point satisfies $3x+5y<7$ and the point $B=\left(\dfrac{3}{2},\dfrac{1}{2}\right)$ attains $3x+5y=7$, the value $m=7$ is indeed the minimum value of $Z$ on the feasible region and it occurs at $B$.
Final Result
$$\boxed{ \displaystyle Z_{\min}=7\quad\text{at}\quad\left(\frac{3}{2},\frac{1}{2}\right) }$$
Find more solved NCERT problems and download notes by Anand Classes — perfect for JEE and CBSE preparation with clear step-by-step explanations and helpful practice tables.
NCERT Question.5 : Maximise $$Z=3x+2y$$ subject to $$x+2y\le 10, \;3x+y\le 15, \;x\ge 0,\quad y\ge 0$$
Solution
Feasible region lies in the first quadrant because $x\ge 0$ and $y\ge 0$. The region is determined by the two lines $x+2y=10$ and $3x+y=15$ together with the coordinate axes.
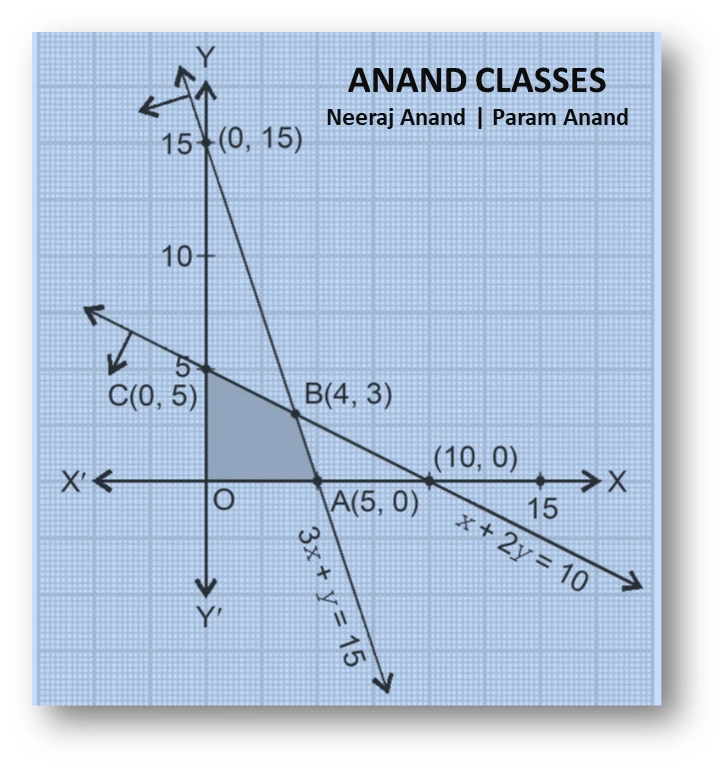
Tables of intercepts for the boundary lines
For the line $x+2y=10$:
| $x$ | $0$ | $10$ |
|---|---|---|
| $y$ | $5$ | $0$ |
So the line joins points $(0,5)$ and $(10,0)$.
For the line $3x+y=15$:
| $x$ | $0$ | $5$ |
|---|---|---|
| $y$ | $15$ | $0$ |
So the line joins points $(0,15)$ and $(5,0)$. (Note the feasible intersection with the first quadrant uses $(0,5)$ and $(5,0)$ as relevant intercepts because of the other constraint.)
Test the origin $(0,0)$ in each inequality:
- $x+2y\le10$ gives $0\le10$, true.
- $3x+y\le15$ gives $0\le15$, true.
Thus both half-planes include the origin, so the feasible region lies on the origin side of each boundary.
The corner (extreme) points of the feasible polygon in the first quadrant are
$$A=(5,0),\quad B=(4,3),\quad C=(0,5).$$
Intersection point $B$ of the two lines
Solve
$$x+2y=10\quad\text{and}\quad 3x+y=15.$$
From $3x+y=15$ we get $y=15-3x$. Substitute into $x+2y=10$:
$$x+2(15-3x)=10\implies x+30-6x=10\implies -5x=-20\implies x=4.$$
Then $y=15-3\cdot4=3$. Hence $B=(4,3)$.
Evaluate $Z=3x+2y$ at corner points
| Corner point | Coordinates | $Z=3x+2y$ |
|---|---|---|
| $A$ | $(5,0)$ | $3\cdot5+2\cdot0=15$ |
| $B$ | $(4,3)$ | $3\cdot4+2\cdot3=12+6=18$ |
| $C$ | $(0,5)$ | $3\cdot0+2\cdot5=10$ |
Among these, the largest value is $18$ at $B=(4,3)$.
Final Result
$$\boxed{\displaystyle Z_{\max}=18\quad\text{at}\quad(4,3)}$$
Download complete solved NCERT sets by Anand Classes for step-by-step linear programming methods, clear tables, and more practice — ideal for JEE and CBSE exam preparation with high-quality study material.


