Co-Ordinate Geometry | Distance Formula, Mid-Point Formula, Section Formula, Slope Formula, Area of Triangle, Centroid of Triangle, Collinearity of Three Points | Solved Examples, FAQs

📚 Introduction to Co-Ordinate Geometry – Class 11 Math

📝 Author: Neeraj Anand
🏛 Published by: ANAND TECHNICAL PUBLISHERS
📖 Available at: ANAND CLASSES

🔍 For CBSE Board & JEE Mains/Advanced Aspirants

📌 What is Co-Ordinate Geometry?

Co-ordinate Geometry, also known as Analytical Geometry, is the study of geometry using a coordinate system. It connects algebra and geometry, making it a powerful tool for solving problems involving shapes, distances, and slopes.

This chapter is fundamental for students preparing for CBSE Class 11 Board Exams and JEE Mains/Advanced, as it provides essential concepts that are widely used in calculus and higher mathematics.

Coordinate geometry is a branch of mathematics, which is used to represent various geometric figures in a 2-D plane.

Coordinate geometry divides the coordinate plane into four different quadrants, which are the I quadrant, II quadrant, III quadrant, and IV quadrants.

Coordinate Axes

The coordinate axes are the two perpendicular lines that form the basis of the Cartesian plane used to represent the position of a point in the plane. To represent a point in the 2D plane we need 2 coordinate axes and the plane that is formed by the intersection of these axes is called the Cartesian plane.

These lines are:

1. x-axis:
   • It is the horizontal axis.
   • It represents the horizontal direction, with positive values to the right of the origin and negative values to the left.
2. y-axis:
   • It is the vertical axis.
   • It represents the vertical direction, with positive values above the origin and negative values below.

Cartesian Plane

The Cartesian plane is a two-dimensional plane formed by two perpendicular lines x-axis (horizontal line) and y-axis (vertical line). These axes intersect at a point called the origin (0,0), which is the center of the plane. The plane is used to locate points using ordered pairs of numbers, called coordinates (x, y), where:

• x: Represents the position along the x-axis (horizontal direction).
• y: Represents the position along the y-axis (vertical direction).

The Cartesian plane is divided into four regions, called quadrants, based on the signs of xxx and yyy.

Coordinates of a Point

A coordinate of a point is an address, which helps to locate a it in space. For a two-dimensional space, the coordinates of a point are (x, y). Here let us take note of these two important terms.

The coordinates of a point are useful to perform numerous operations of finding distance, midpoint, the slope of a line, and equation of a line.

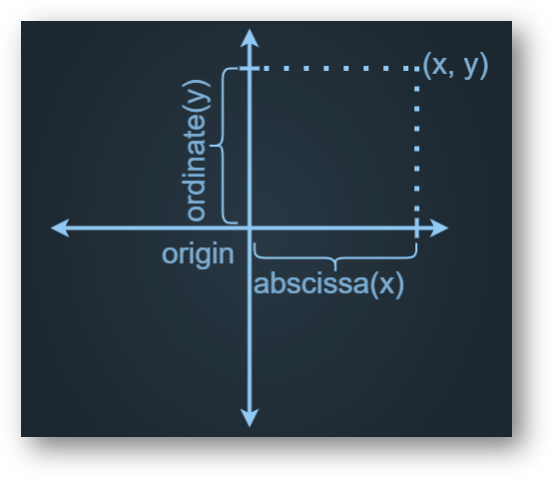
• Origin: Through a point O, referred to as the origin, we take two mutually perpendicular lines XOX’ and YOY’, and call them x and y axes respectively.
• Abscissa & Ordinate: The position of a point is completely determined with reference to these axes by means of an ordered pair of real numbers (x, y) called the coordinates of P where | x | and | y | are the distances of the point P from the y-axis and the x-axis respectively,
  • Abscissa: It is the x value in the point (x, y), and is the distance of this point along the x-axis, from the origin.
  • Ordinate:  It is the y value in the point (x, y)., and is the perpendicular distance of the point from the x-axis, which is parallel to the y-axis.

Coordinate Geometry Formulas

The formulas of coordinate geometry help in conveniently proving the various properties of lines and figures represented in the coordinate axes. The formulas of coordinate geometry are

• Distance Formula
• Mid-Point Formula
• Section Formula
• Slope Formula
• Area of Triangle

Let us know more about each of the formulas in the below paragraphs.

Distance Formula

The distance between two points A(x₁, y₁) and B(x₂, y₂) is given
AB = √((x₂ – x₁)² + (y₂ – y₁)²)

The distance of the point P(x, y) from the origin O(0, 0) is
OP = √((x – 0)²+ (y – 0)²), i.e. OP = √(x² + y²)

Example: Find the distance between the points P(-4, 7) and Q(2, -5).
Solution:

The given points are P(-4, 7) and Q(2, -5).

Then, (x₁ = -4, y₁ = 7) and (x₂ = 2, y₂ = -5). : 

PQ =  √((x₂ – x₁)² + (y₂ – y₁)²)
= √((2 – (-4))² + (-5 – 7)²)
= √(6² + (-12)²
= √(36 + 144)
= √180 
= 6√5 

Mid-Point Formula

The midpoint is the point that divides any line segment into two equal parts. The formula to find the midpoint of the line with endpoints A(x₁, y₁) and B(x₂, y₂) is given by,

midpoint (x,y) = {(x₁+x₂)/2 , (y₁+y₂)/2}

Example: Find the coordinates of the midpoint of the line segment joining points A(-5, 4) and B(7,-8).

Solution:

Let M(x, y) be the midpoint of AB. Then, 
x = ((-5) + 7)/2 =1 and  y = ((4 + (-8)) = -2

Hence, the required point is M (1, -2).

Section Formula

The coordinates of the point P(x, y) which divides the line segment joining A(x₁, y₁) and B(x₂, y₂) internally in the ratio m:n are given by 

x = (mx₂ + nx₁) / (m+n)

y = (my₂+ny₁) / (m+n)

Example: Find the coordinates of the point that divides the line segment joining the points A(5, 4) and B(7,8) in the ratio of 2:3.

Solution:

Let M(x, y) be the required point,
given m:n = 2:3 and (x₁, y₁) = (5, 4) , (x₂, y₂) = (7,8)

now for M(x,y)

x = (mx₂ + nx₁) / (m+n)
= (2×7 + 3×5)/(2 + 3)
= 29/5

y = (my₂+ny₁) / (m+n)
= (2×8 + 3×4)/(2 + 3)
= 40/5
= 8

So, the required point M(x,y) is (29/5 , 8)

Slope Formula

The slope of a line is the inclination of the line. Slope Formula is calculated by measuring the angle made by the line with the positive x-axis, or by calculating it using any two points on the line. The slope of a line inclined at an angle θ with the positive x-axis is given by m = tan θ.  The slope of a line joining the two points A(x₁, y₁) and B(x₂, y₂) is given by

m = tan θ = (y₂-y₁) / (x₂-x₁)

Example: Find the slope of the line segment joining by points A(5, 1) and B(7,8).

Solution:

given,  (x₁, y₁) = (5, 1) , (x₂, y₂) = (7, 8)

Slope (m) = (y₂-y₁) / (x₂-x₁)
= (8-1)/(7-5)
= 7/2

Area of Triangle

The area of a triangle ABC with vertices A(x₁, y₁), B(x₂, y₂), and C(x₃, y₃) is given by 

area(ABC) = |1/2 {x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃ (y₁ – y₂)}|

Example: Find the area of the triangle whose vertices are A(2, 7), B(3, -1), and C(-5, 6).

Solution:

Let A(2, 7), B(3, -1) and C(-5, 6) be the vertices of the given △ABC.

Then,
(x₁ = 2, y₁ = 7), (x₂ = 3, y₂ = -1) and (x₃ = -5, y₃ = 6). 

Area of △ABC =  |1/2 {x₁(y₂ – y₃) + x₂(y₃ – y₁) + x3 (y₁ – y₂)}|

= 1/2 |2(-1 – 6) + 3(6 – 7) – 5(7 +1)|
= 1/2| -14 – 3 – 40|
= 1/2|-57|
= 57/
= 28.5 sq units.

Condition for Collinearity of Three Points

Let the given points be A(x₁, y₁), B(x₂, y₂), and C(x₃, y₃). Then A, B, and C are collinear,

 area of ABC = 0
1/2[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)] = 0

OR

Slope of AB = Slope of BC

Example: Show that points A(-1, 1), B(5, 7), and C(8,10) are collinear.

Solution: 

Let A(-1, 1), B(5, 7) and C(8, 10) be the given points. 

Then, (x₁ = -1, y₁ = 1), (x₂ = 5, y₂ = 7) and (x₃ = 8, y₃ = 10)

∴  x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)

= (-1) (7 – 10) + 5(10 -1) + 8(1 – 7) 
= (3 + 45 – 48)
= 0 

Hence, the given points are collinear. 

Centroid of a Triangle

Centroid of a triangle is the point of intersection of all three medians of a triangle. The centroid of a triangle having its vertices A(x₁,y₁), B(x₂,y₂), and C(x₃,y₃) is given by the formula

Centroid (x,y) = {(x₁+x₂+x₃) / 3, (y₁+y₂+y₃) / 3}

Example: Find the centroid of the triangle whose vertices are A(2, 7), B(3, -1), and C(-5, 6).

Solution:

Let A(2, 7), B(3, -1) and C(-5, 6) be the vertices of the given △ABC.

(x₁ = 2, y₁ = 7), (x₂ = 3, y₂ = -1) and (x₃ = -5, y₃ = 6).

Centroid (x,y) = {(x₁+x₂+x₃) / 3 , (y₁+y₂+y₃) / 3}

= {2+3+(-5)}/3 , {7+(-1)+6}/3
= (0 , 12)

📌 Importance of Co-Ordinate Geometry in JEE & CBSE Board Exams

✅ Concept-Based & Logical Approach – Unlike pure algebra, coordinate geometry requires logical visualization.
✅ High-Scoring Topic in JEE – Questions from this topic frequently appear in JEE Mains & Advanced.
✅ Foundation for Calculus & Vectors – Essential for higher mathematics in Class 12 and beyond.
✅ Real-Life Applications – Used in engineering, physics, computer graphics, and navigation.

FAQs on Coordinate Geometry

What is meant by Cartesian Plane?

The space is assumed to consist of an imaginary plane, to study the coordinate geometry. this imaginary plane is called the Cartesian plane. It is formed by two perpendicular lines the x-axis (horizontal axis) and the y-axis (vertical axis).

What is the importance of Coordinate Geometry?

Coordinate geometry is of great importance in our life. It is used by us on a daily basis which includes:

• GPS and Map Navigation uses coordinate geometry to mark our location.
• It used by airline industry to plot the trajectory of a plane.
• Latitude and Longitude system uses coordinate geometry to work.
• It is also used for military purposes.

What is meant by Abscissa and Ordinates in Coordinate Geometry?

Abscissa and Ordinate represent the position of a point on the plane. Horizontal component or the value at X-axis is called the abscissa while the vertical component or the value at Y-axis is called the ordinate. For example, in the point (7, 9), 7 is the abscissa and 9 is the ordinate.

What is the coordinate of a point?

The ordered pair (x,y) which is used to know the position of any point in the Cartesian plane is called the coordinate point. For example,(1,3) is a coordinate point.

📖 Key Concepts Covered

✔️ Cartesian Coordinate System – Understanding the X and Y axes
✔️ Distance Formula – Finding the distance between two points
✔️ Section Formula – Dividing a line segment in a given ratio
✔️ Midpoint Formula – Finding the midpoint of a line segment
✔️ Slope of a Line – Understanding gradients and inclination
✔️ Equation of a Line – Different forms of equations (slope-intercept, two-point, etc.)
✔️ Applications in JEE and Competitive Exams

📥 Download the PDF for Complete Study Material!

📘 “Introduction to Co-Ordinate Geometry” by Neeraj Anand (ANAND CLASSES) is a must-have book for mastering this topic. It includes:
✔️ Detailed Theory & Concepts
✔️ Solved Examples & Practice Questions
✔️ JEE & CBSE Board-Level Problems
✔️ Shortcuts & Tricks for Quick Solving

📥 Download Now & Boost Your Exam Preparation!

🚀 Start Your Journey to JEE Success Today!