Anand Classes offers detailed and accurate Linear Inequalities Miscellaneous Exercise NCERT Solutions Class 11 Maths Chapter 5 (Set-1) to help students strengthen their understanding of linear inequalities and their graphical representation. These step-by-step solutions are prepared according to the latest NCERT and CBSE syllabus, ensuring conceptual clarity and exam-focused learning. Ideal for Class 11 students, these solutions make it easier to grasp challenging concepts and solve all types of inequality problems effectively. Click the print button to download study material and notes.
NCERT Question 1 : Solve the inequality:
$$2 \le 3x – 4 \le 5$$
Solution :
Given:
$$2 \le 3x – 4 \le 5$$
Add $4$ to all parts:
$$2 + 4 \le 3x – 4 + 4 \le 5 + 4$$
$$6 \le 3x \le 9$$
Divide all parts by $3$:
$$\frac{6}{3} \le \frac{3x}{3} \le \frac{9}{3}$$
$$2 \le x \le 3$$
Thus, the solution set is:
$$x \in [2, 3]$$
High-quality study content for CBSE & JEE by Anand Classes — boost your exam preparation!
NCERT Question 2 : Solve the inequality:
$$6 \le -3(2x – 4) < 12$$
Solution :
Given:
$$6 \le -3(2x – 4) < 12$$
Divide the entire inequality by $3$:
$$\frac{6}{3} \le – (2x – 4) < \frac{12}{3}$$
$$2 \le -(2x – 4) < 4$$
Multiply by $-1$ (reverse inequality signs):
$$-2 \ge 2x – 4 > -4$$
Add $4$ to all parts:
$$-2 + 4 \ge 2x – 4 + 4 > -4 + 4$$
$$2 \ge 2x > 0$$
Divide by $2$:
$$1 \ge x > 0$$
Thus, the solution set is:
$$x \in (0, 1]$$
Top-quality exam-focused math notes by Anand Classes — perfect for Class 11 & competitive exams!
NCERT Question 3 : Solve the inequality:
$$-3 \le 4 – \frac{7x}{2} \le 18$$
Solution :
Given:
$$-3 \le 4 – \frac{7x}{2} \le 18$$
Subtract $4$ from each part:
$$-3 – 4 \le 4 – \frac{7x}{2} – 4 \le 18 – 4$$
$$-7 \le -\frac{7x}{2} \le 14$$
Multiply each part by $-2$ (reverse inequality signs):
$$14 \ge 7x \ge -28$$
Rewrite in standard increasing order:
$$-28 \le 7x \le 14$$
Divide by $7$:
$$-4 \le x \le 2$$
Thus, the solution set is:
$$x \in [-4, 2]$$
Accurate step-by-step Math notes — ideal for Class 11 preparation by Anand Classes!
NCERT Question 4 : Solve the inequality:
$$-15 < \frac{3(x – 2)}{5} \le 0$$
Solution :
Given:
$$-15 < \frac{3(x – 2)}{5} \le 0$$
Multiply every part by $5$:
$$-75 < 3(x – 2) \le 0$$
Divide every part by $3$:
$$-25 < x – 2 \le 0$$
Add $2$ to each part:
$$-25 + 2 < x – 2 + 2 \le 0 + 2$$
$$-23 < x \le 2$$
Thus, the solution set is:
$$x \in (-23, 2]$$
Perfect for Class 11 Linear Inequalities practice — powered by Anand Classes study material!
NCERT Question 5 : Solve the inequality:
$$-12 < 4 – \frac{3x}{-5} \le 2$$
Solution :
Given:
$$-12 < 4 – \frac{3x}{-5} \le 2$$
Rewrite the term:
$$-\frac{3x}{-5} = \frac{3x}{5}$$
So the inequality becomes:
$$-12 < 4 + \frac{3x}{5} \le 2$$
Subtract $4$ from all parts:
$$-12 – 4 < \frac{3x}{5} \le 2 – 4$$
$$-16 < \frac{3x}{5} \le -2$$
Multiply each part by $5$:
$$-80 < 3x \le -10$$
Divide every part by $3$:
$$-\frac{80}{3} < x \le -\frac{10}{3}$$
Final Solution
$$x \in \left(-\frac{80}{3}, -\frac{10}{3}\right]$$
Enhance your Class 11 Maths preparation with high-quality inequality solutions by Anand Classes — ideal for CBSE and competitive exams!
NCERT Question 6 : Solve the inequality:
$$7 \le \frac{3x + 11}{2} \le 11$$
Solution :
Given:
$$7 \le \frac{3x + 11}{2} \le 11$$
Multiply each part by $2$:
$$14 \le 3x + 11 \le 22$$
Subtract $11$ from all parts:
$$3 \le 3x \le 11$$
Divide each part by $3$:
$$1 \le x \le \frac{11}{3}$$
Final Solution
$$x \in \left[1, \frac{11}{3}\right]$$
For more well-structured Class 11 Maths solutions with Anand Classes — perfect for CBSE and competitive exam preparation!
NCERT Question 7 : Solve the inequalities and represent the solution on the number line:
$$5x + 1 > -24 \quad \text{and} \quad 5x – 1 < 24$$
Solution :
Given:
$$5x + 1 > -24 \quad \text{and} \quad 5x – 1 < 24$$
Solving First Inequality:
$$5x + 1 > -24$$
$$5x > -24 – 1$$
$$5x > -25$$
$$x > -5 \quad \dots (i)$$
Solving Second Inequality:
$$5x – 1 < 24$$
$$5x < 24 + 1$$
$$5x < 25$$
$$x < 5 \quad \dots (ii)$$
Combined solution:
From (i) and (ii):
$$-5 < x < 5$$
So,
$$x \in (-5, 5)$$
Number Line Representation:
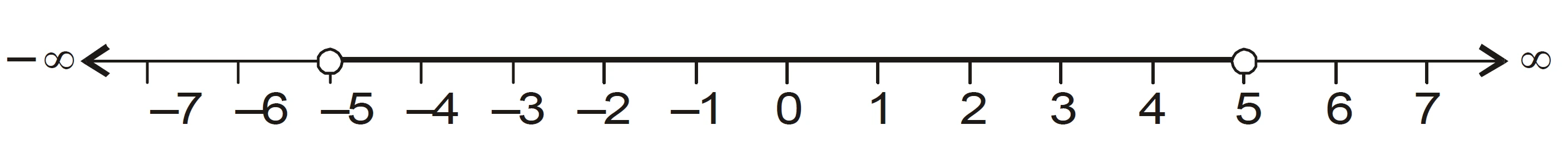
For more CBSE Class 11 Maths solutions with proper LaTeX formatting, stay connected with Anand Classes — your trusted study partner for board exams and competitive success!


